تبدیل دودویی (یا باینری) به اعشاری (یا دسیمال) از اعداد در ستون های وزنی برای تعیین ترتیب ارقام و در نتیجه تعیین مقدار نهایی عدد استفاده میکند.
دستگاه اعداد باینری، پایه و اساس سیستم های دیجیتال کامپیوتری را تشکیل میدهند، از این رو تبدیل اعداد باینری (پایه دو) به اعداد اعشاری (پایه ده) و همچنین تبدیل اعداد اعشاری به اعداد باینری، از اهمیت بسیاری برخوردار است.
دستگاه اعداد اعشاری یا دسیمال (Decimal) از سیستم شماره گذاری بر مبنای ده (Base-of-10) استفاده میکند، که در آن هر یک از ارقام تشکیل دهنده عدد نهایی، میتواند یکی از ده مقدار ممکن بین 0 تا 9 را اختیار کند.
در سیستم اعداد اعشاری علاوه بر داشتن ۱۰ رقم مختلف برای هر حالت (۹ تا ۰) امکان اعمال عملیات های ریاضی از جمله ضرب، تقسیم، تفریق و جمع نیز فراهم است.
در این دستگاه ارزش هر رقم، ده برابر بیشتر از رقم قبلی خود است. برای مثال در عدد ۲۱۳ ارزش مکانی رقم ۱ ده برابر ارزش مکانی عدد ۳ است.
دستگاه عددی اعشاری از مجموعهای از نمادهای q و b جهت تعیین و مشخص کردن وزن (Weight) هر رقم استفاده میکند. برای مثال براساس تعاریف فوق، رقم 6 در عدد 60 وزن کمتری نسبت به رقم 6 در عدد 600 خواهد داشت.
تمامی سیستم های شماره گذاری را میتوان طبق رابطهی ریاضی زیر به صورت خلاصه بیان کرد:
![]()
که در آن N یک عدد حقیقی مثبت، b رقم، q مبنای عدد و i عددی صحیح است که میتواند مقادیر مثبت، منفی و یا صفر را اختیار کند.
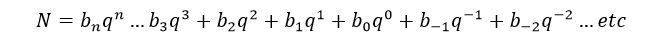
سیستم شماره گذاری دسیمال
در سیستم شماره گذاری دسیمال (مبنای ده)، ارقام یک عدد به ترتیب از سمت راست به چپ دارای ارزش مکانی یکان، صدگان، هزارگان و … هستند. به زبان ریاضی ارقام یک عدد به ترتیب از راست به چپ ضرایبی از ۱۰۰, ۱۰۱, ۱۰۲, ۱۰۳ و … هستند. در اعداد اعشاری، موقعیت ارقام در سمت چپ ممیز ضرایبی از توان مثبت ۱۰ و به همین ترتیب در سمت راست ممیز با حرکت از سمت چپ به راست، وزن هر رقم، ضرایبی از توان منفی ۱۰ مانند ۱۰-۱, ۱۰-۲, ۱۰-۳و غیره خواهد بود.
در سیستم شماره گذاری دسیمال موقعیت هر رقم نشان دهنده وزن آن رقم بر مبنای 10 (modulo-10) است. بنابراین به منظور تعریف سیستم شماره گذاری دسیمال طبق رابطه ریاضی فوق کافیست q برابر 10 قرار گیرد.
مانند: عدد 400 معادل 4x 10۲ و یا 20 معادل 2x 10۱.
هر عدد دسیمال با مجموع، حاصل ضرب هر یک از ارقام آن عدد در وزن همان رقم مشخص برابر است. برای مثال عدد N = ۶۱۶۳۱۰
از راست به چپ رقم ۳ دارای وزن۱۰۰، عدد ۶ دارای وزن ۱۰۱، عدد ۱ دارای وزن ۱۰۲ و در نهایت عدد ۶ با وزن ۱۰۳. ضرب هر عدد در وزن مخصوصش و جمع تمامی ارقام، معادل با عدد اعشاری اولیه خواهد بود.
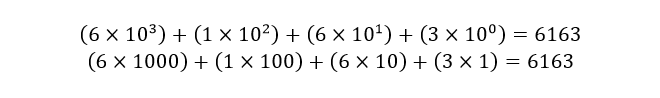
در این سیستم اولین رقم از سمت چپ دارای بیشترین وزن و ارزش مکانی (most significant digit, or MSD) و اولین رقم از سمت راست دارای کمترین وزن و ارزش مکانی (least significant digit or LSD) خواهد بود. به عبارت دیگر در مثال قبل عدد 6 دارای بیشترین وزن یا MSD و عدد 3 کمترین وزن یا همان LSD است.
سیستم شماره گذاری باینری
سیستم شماره گذاری باینری یکی از اساسی ترین سیستم های شماره گذاری در تمام سیستم های دیجیتال و کامپیوترها است. دستگاه اعداد باینری از قوانین ریاضی مشابه حاکم بر دستگاه اعداد دسیمال تبعیت میکنند. اما برخلاف سیستم اعداد اعشاری که بر مبنای ۱۰ است، دستگاه اعداد باینری از توانهای ۲ استفاده میکند. سیستمهای دیجیتال و کامپیوترها جهت نمایش یک وضعیت، تنها از دو حالت (منطق ۰ و منطق ۱) استفاده میکنند و هر رقم ۰ و ۱ به عنوان یک رقم واحد بر مبنای ۲ (سیستم شماره گذاری باینری) در نظر گرفته میشود.
برای مثال عدد باینری 101100101 توسط رشتهای از ارقام 0 و1 معرفی میشود که هر رقم در طول رشته با حرکت از سمت راست به چپ دارای دو برابر ارزش رقم قبل خود است. از آن جایی که در سیستم های دیجیتال هر رقم تنها میتواند دو وضعیت مختلف (0 و1) داشته باشد، q برابر 2 خواهد بود.
از طرفی به علت تبدیل اعداد اعشاری به اعداد باینری، در این اعداد نیز هر رقم دارای وزن و ارزش مکانی منحصر به خود است. اولین رقم از سمت چپ بیت، با ارزشترین و پر وزنترین بیت (Most Significant Bit-MSB) و اولین رقم از سمت راست کم ارزشترین بیت (Least Significant Bit-LSB) است.
در ادامه روش های تبدیل اعداد باینری به اعداد دسیمال و برعکس بررسی خواهند شد.
نمایش اعداد باینری

در دستگاه اعداد اعشاری، وزن هر رقم از سمت راست به چپ ۱۰ برابر افزایش مییابد، این در حالی است که در دستگاه اعداد باینری وزن هر رقم از سمت راست به چپ ۲ برابر وزن رقم قبل خود خواهد بود. بنابراین با توجه به تعریف فوق در یک عدد باینری، وزن رقم اول برابر با ۱ (۲۰)، رقم دوم دارای وزن ۲ (۲۱)، رقم سوم دارای وزن ۴ (۲۲)، رقم چهارم دارای وزن ۸ (۲۳) و … خواهد بود.
برای مثال تبدیل یک عدد باینری به عدد دسیمال به شرح زیر است:

از سمت راست به چپ با محاسبه حاصل مجموع تمام ارقام دسیمال در مکان هایی که دارای معادل مقدار باینری برابر ۱ هستند، عدد دسیمال مربوطه به صورت زیر حاصل میشود.
![]()
در سیستمهای تبدیل اعداد معمولا از زیر نویس به منظور نشان دادن سیستم شماره گذاری (پایه مربوطه) استفاده میشود. برای مثال :
![]()
در مواردی که پس از عدد از زیر نویس استفاده نشود، عموما عدد، دسیمال (پایه ۱۰) فرض میشود.
روش تقسیم های بر ۲ متوالی
تا به اینجا، نحوه تبدیل اعداد باینری به اعداد دسیمال شرح داده شده است، در ادامه چگونگی تبدیل اعداد اعشاری (دسیمال) به اعداد باینری بررسی خواهد شد. روش تقسیم های متوالی بر دو یکی از متداول ترین روش ها جهت تبدیل اعداد دسیمال به اعداد باینری است. در این روش عدد دسیمال به صورت متوالی بر دو تقسیم خواهد شد تا زمانی که خارج قسمت برابر صفر شود. به عنوان مثال تبدیل عدد اعشاری به معادل باینری آن در ادامه بررسی خواهد شد.
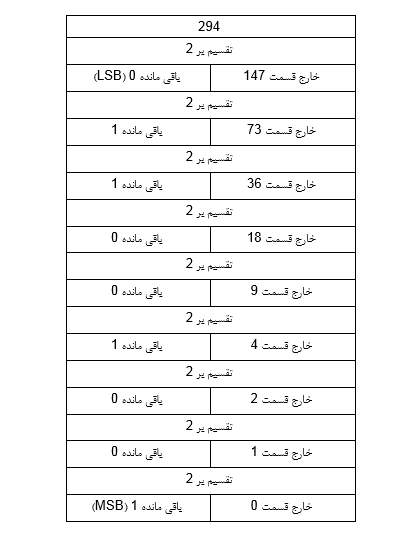
در تقسیم هر عدد دسیمال بر عدد ۲ مطابق توضیحات فوق یک خارج قسمت و یک باقیمانده مشاهده خواهد شد. در صورتی که مقسوم عدد دسیمال زوج باشد، باقی مانده تقسیم آن بر ۲ برابر صفر و اگر مقسوم فرد باشد باقی مانده برابر عدد یک خواهد بود. از کنار هم قرار دادن تمام باقی مانده ها به ترتیب از آخرین باقی مانده به اول معادل باینری عدد دسیمال بدست خواهد آمد.
بر اساس این روش معادل عدد اعشاری ۲۹۴۱۰ برابر با ۱۰۰۱۰۰۱۱۰۲ خواهد بود. از روش تقسیم های متوالی به منظور تبدیل اعداد به مبناهایی غیر از ۲ نیز میتوان استفاده کرد.
با توجه به تعریف اعداد باینری هر رقم یا بیت میتوان تنها یکی از دو مقدار 0 یا 1 را اختیار کند. این خصوصیت یکی از ویژگی های مهم سیستم شماره گذاری باینری به نام مجموع وزن ها را معرفی میکند. در این روش با حرکت از سمت LSB ارزش هر بیت دو برابر بیت قبلی خواهد بود.
بنابراین اعداد اعشاری با استفاده از هر دو روش مجموع وزن ها و یا تقسیم های متوالی بر ۲ میتوانند به اعداد باینری تبدیل شوند در حالی که جهت تبدیل اعداد باینری به اعداد دسیمال تنها میتوان از روش مجموع وزن ها استفاده کرد.
پیشوند ها و اصطلاحات اعداد باینری
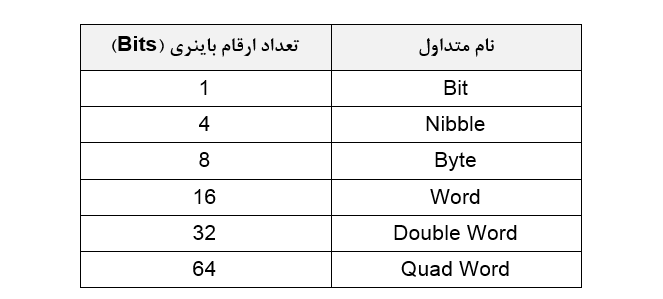
اعداد باینری ، را مانند اعداد دسیمال میتوان به راحتی از هم کم و یا با یکدیگر جمع کرد که بسته به تعداد بیت های مورد استفاده نتیجه این عملیات ها اندازه های مختلفی را اختیار میکنند. به طور معمول اعداد باینری در سه قالب بیت (Bit)، بایت (Byte) و کلمه (Word) وجود دارند. هر بیت تنها یک رقم باینری، هر بایت 8 رقم باینری و یک کلمه شامل 16 رقم باینری خواهد بود.
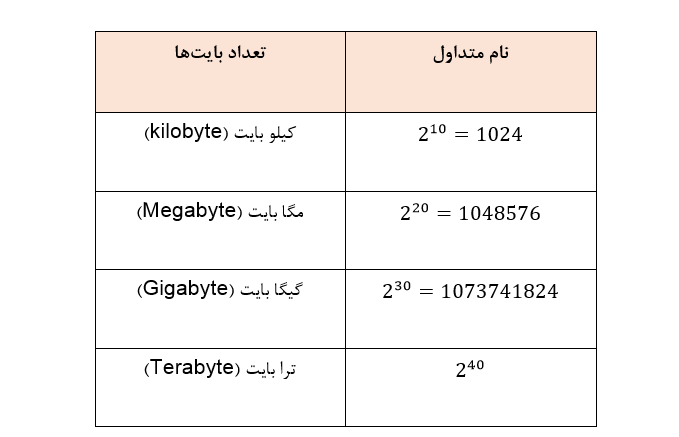
طبقه بندی و دسته بندی بیت ها به گروه هایی بزرگتر عموما با نامهای رایج زیر انجام میشود.
یکی از نکات مهم در تبدیل اعداد باینری به دسیمال و یا اعداد دسیمال به اعداد باینری، دقت و توجه به مبنای اعداد مورد استفاده است. برای مثال فراموش کردن مبنای عدد ۱۰ سبب میشود آن را به دو شکل مختلف خواند. در صورتی که فرض شود مبنای عدد ۱۰ است عدد فوق ده خوانده میشود. اما اگر مبنای عدد، ۲ فرض شود، با توجه به وزن ارقام معادل باینری عدد ۲ خواهد بود.
به منظور جلوگیری از اشتباهات رایج در این زمینه، نوشتن مبنای عدد به صورت، یک عدد کوچک پس از آخرین رقم پیشنهاد شده است. این عدد با عنوان زیر نویس (Subscript) شناخته میشود. بنابراین در مثال قبل، اگر عدد مشخص شده باینری باشد کافیست با اضافه کردن زیر نویس 2 مبنای عدد به صورت ۱۰۲ نمایش داده شود، همچنین در صورتی که عدد دسیمال باشد، مبنای آن به صورت زیر نویس ۱۰۱۰ نمایش داده خواهد شد.
امروز با افزایش کاربرد و پیشرفت سیستمهای میکروکنترلر (micro-controller) و یا ریز پردازنده ها (microprocessor)، مفهوم بیت جای خود را به بایت داده است. با کنار هم قرار گرفتن 8 بیت یک بایت تولید خواهد شد. اکثر سخت افزارهای رایانهای مانند هارد دیسک ها (hard drives) و ماژول های حافظه، اندازه هایی در حد چند مگابایت و یا گیگابایت را اختیار میکنند.
خلاصه تبدیل اعداد باینری به دسیمال
کلمه بیت (BIT) مخفف عبارت (BInary digiT) است.
در سیستم اعداد باینری تنها دو وضعیت ممکن (منطق ۰ و منطق ۱) برای هر رقم وجود دارد.
در سیستم اعداد دسیمال، ۱۰ حالت ممکن (۰ تا ۹) برای هر رقم وجود دارد.
در سیستم اعداد باینری از سمت راست به چپ ارزش وزنی هر رقم دو برابر رقم قبل خود خواهد شد.
با استفاده از دو روش تقسیم های متوالی بر ۲ و روش مجموع وزن ها میتوان یک عدد اعشاری را به یک عدد باینری تبدیل کرد.
جهت جلوگیری از خطاهای احتمالی، یادداشت کردن مبنای اعداد به صورت زیرنویس در هنگام تبدیل اعداد باینری به دسیمال و بالعکس، پیشنهاد شده است.
تبدیل اعداد باینری به دسیمال و یا تبدیل اعداد دسیمال به اعداد باینری به روش های مختلفی صورت میپذیرد. یکی از نکات مهم در هنگام تبدیل اعداد دسیمال به اعداد باینری تشخیص کم ارزشترین بیت (LSB) و پر ارزشترین بیت (MSB) است.


دیدگاه خود را بنویسید