طراحی فیلتر باترورث

تعدادی از «توابع تقریبی» در طراحی فیلتر آنالوگ خطی وجود دارد که از یک رویکرد ریاضی برای بهترین تقریب تابع انتقال مورد نیاز برای طراحی فیلترها استفاده می‌کنند. برخی از چنین طرح‌هایی با نام‌های بیضوی، باترورث، چبیشف، بسل، کاور و غیره شناخته می‌شوند

در مقالات فیلترهای قبلی، فیلترهای درجه اول پایین‌گذر و بالاگذر ساده را بررسی کردیم که حاوی تنها یک مقاومت و یک جز راکتانسی (یک خازن) در طراحی مدار فیلتر RC خود بودند.

در‌کاربردهایی مانند ارتباطات یا سیستم‌های کنترل که از فیلترها برای شکل دادن به طیف فرکانس سیگنال استفاده می‌کنند، شکل یا عرض قسمت شیب‌دار که «باند انتقال» نیز نامیده می‌شود، برای یک فیلتر ساده درجه اول ممکن است خیلی طولانی باشد بنابراین فیلترهای طراحی شده اکتیو با بیش از یک «درجه» مورد نیاز است. این نوع فیلترها معمولا به عنوان فیلترهای درجه بالا یا درجه n شناخته می‌شوند.

پیچیدگی یا نوع فیلتر با «درجه» فیلترها مشخص می‌شود و به تعداد اجزای راکتیو مانند خازن‌ها یا سلف‌ها در طراحی آن بستگی دارد. همچنین می‌دانیم که شیب قسمت شیب‌دار و در نتیجه عرض باند انتقال به درجه فیلتر بستگی دارد و برای یک فیلتر ساده درجه اول استاندارد، شیب قسمت شیب‌دار برابر با ۲۰ دسی‌بل بر دهه یا ۶ دسی‌بل بر اکتاو است.

پس، برای فیلتری که دارای درجه n است، شیب قسمت شیبدار برابر با  دسی‌بل بر دهه یا  دسی‌بل بر اکتاو خواهد بود. بنابراین یک فیلتر درجه اول دارای شیب قسمت شیب‌دار 20 دسی‌بل در دهه (6 دسی‌بل در اکتاو)، یک فیلتر درجه دوم دارای شیب قسمت شیب‌دار 40 دسی‌بل در دهه (12 دسی‌بل در اکتاو) و یک فیلتر درجه چهارم دارای شیب قسمت شیب‌دار 80 دسی‌بل در دهه (24 دسی‌بل در اکتاو) است و غیره.

فیلترهای درجه بالا مانند درجه سوم، چهارم و پنجم معمولا با کسکود کردن فیلترهای درجه اول و درجه دوم تشکیل می‌شوند.

 به عنوان مثال، دو فیلتر پایین‌گذر درجه دوم را می‌توان با هم کسکود کرد تا یک فیلتر پایین‌گذر درجه چهارم تولید شود. اگرچه هیچ محدودیتی برای درجه فیلتر وجود ندارد، اما با افزایش درجه، اندازه و هزینه آن نیز افزایش می‌یابد و با کاهش دقت همراه است.

دهه و اکتاو

آخرین کلام در مورد دهه‌ها و اکتاوها این است که در مقیاس فرکانس، یک دهه یک افزایش ده برابری (ضرب در ۱۰) یا ده برابر کاهش (تقسیم بر ۱۰) است. به عنوان مثال، ۲ تا ۲۰ هرتز نشان‌دهنده یک دهه است، در حالی که ۵۰ تا ۵۰۰۰ هرتز نشان‌دهنده دو دهه است (۵۰ تا ۵۰۰ هرتز و سپس ۵۰۰ تا ۵۰۰۰ هرتز).

 اکتاو دو برابر شدن (ضرب در ۲) یا نصف شدن (تقسیم بر ۲) مقیاس فرکانس است. به عنوان مثال، ۱۰ تا ۲۰ هرتز نشان دهنده یک اکتاو است، در حالی که ۲ تا ۱۶ هرتز سه اکتاو (۲ تا ۴، ۴ تا ۸ و در نهایت ۸ تا ۱۶ هرتز) است که فرکانس را هر بار دو برابر می‌کند. در هر صورت، مقیاس‌های لگاریتمی به‌طور گسترده در حوزه فرکانس برای نشان دادن مقدار فرکانس، هنگام کار با تقویت‌کننده‌ها و فیلترها استفاده می‌شوند، بنابراین درک آنها مهم است.

مقیاس فرکانسی لگاریتمی

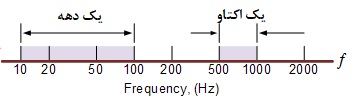۱. مقیاس فرکانسی لگاریتمی

از آنجایی که مقاومت‌ها و خازن‌های تعیین‌کننده فرکانس همگی برابر هستند، فرکانس قطع یا گوشه (ƒC) برای یک فیلتر درجه اول، دوم، سوم یا حتی یک فیلتر درجه چهارم نیز باید برابر باشد و با استفاده از معادله آشنای قدیمی ما این‌گونه به دست می‌آید:

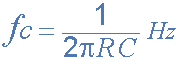
همانند فیلترهای درجه اول و دوم، فیلترهای بالا‌گذر درجه سوم و چهارم به سادگی با تعویض موقعیت اجزای تعیین‌کننده فرکانس (مقاومت‌ها و خازن‌ها) در فیلتر پایین‌گذر معادل تشکیل می‌شوند. فیلترهای درجه بالا را می‌توان با پیروی از روش‌هایی که قبلا در آموزش فیلترهای پایین‌گذر و بالاگذر مشاهده کردیم، طراحی کرد. با این حال، گین کلی فیلترهای درجه بالا ثابت است زیرا تمام اجزای تعیین‌کننده فرکانس برابر هستند.

تقریب فیلتر

تاکنون مدارهای فیلتر درجه اول پایین‌گذر و بالاگذر، پاسخ فرکانسی و شیفت فاز حاصل از آنها را بررسی کرده‌ایم. یک فیلتر ایده‌آل مشخصاتی همچون حداکثر صافی و گین باند عبور، حداقل تضعیف باند توقف و همچنین یک شیب تیز از باند عبور به باند توقف (باند انتقال) را به ما می‌دهد و بنابراین واضح است که تعداد زیادی از پاسخ‌های شبکه این الزامات را برآورده کند.

بنابراین جای تعجب نیست که تعدادی از «توابع تقریبی» در طراحی فیلتر آنالوگ خطی وجود دارد که از یک رویکرد ریاضی برای بهترین تقریب تابع انتقال مورد نیاز برای طراحی فیلترها استفاده می‌کنند.

برخی از چنین طرح‌هایی با نام‌های بیضوی، باترورث، چبیشف، بسل، کاور و غیره شناخته می‌شوند. از میان این پنج توابع تقریبی «قدیمی» برای فیلتر آنالوگ خطی، تنها فیلتر باترورث و به خصوص طراحی فیلتر پایین‌گذر باترورث در اینجا به عنوان متداول‌ترین تابع مورد استفاده در نظر گرفته می‌شود.

طراحی فیلتر پایین‌گذر باترورث

پاسخ فرکانسی تابع تقریب فیلتر باترورث اغلب به عنوان پاسخ «حداکثر مسطح» (بدون ریپل) نامیده می‌شود زیرا باند عبور طوری طراحی شده است که پاسخ فرکانسی تا حد امکان از صفر هرتز (DC) تا نقطه فرکانس قطع منفی 3 دسی‌بل را بدون ریپل داشته باشد. فرکانس‌های بالاتر از نقطه فرکانس قطع در باند توقف با شیب 20 دسی‌بل در دهه یا 6 دسی‌بل در اکتاو به صفر می‌رسد. دلیل این امر برابر بودن «ضریب کیفیت» یا Q با 707/0 است.

با این حال، زمانی که فیلتر از باند عبور به باند توقف تغییر می‌کند، یکی از معایب اصلی فیلتر باترورث این است که این صافی باند عبور را به قیمت یک باند انتقال گسترده به دست می‌آورد. همچنین مشخصات فازی ضعیفی نیز دارد. پاسخ فرکانسی ایده‌آل، که به عنوان فیلتر «دیوار آجری» نامیده می‌شود، و تقریب‌های استاندارد باترورث برای درجه‌های مختلف فیلتر در زیر آورده شده است.

پاسخ فرکانسی ایده‌آل برای یک فیلتر باترورث

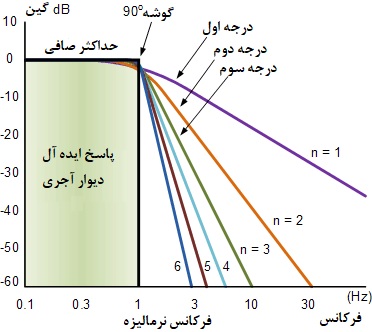۲. پاسخ فرکانسی ایده‌آل برای یک فیلتر باترورث

توجه داشته باشید که هرچه درجه فیلتر باترورث بیشتر باشد، تعداد طبقات کسکود شده در طراحی فیلتر بیشتر است و فیلتر به پاسخ ایده‌آل «دیوار آجری» نزدیکتر می‌شود. اما در عمل، پاسخ فرکانسی ایده آل باترورث دست نیافتنی است زیرا ریپل زیادی در باند عبور ایجاد می‌کند.

معادله تعمیم‌یافته پاسخ فرکانسی یک فیلتر باترورث درجه «n» به صورت زیر نشان داده می‌شود:

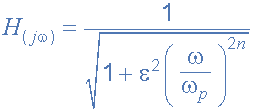
جایی که n نشان‌دهنده درجه فیلتر است، امگا ω برابر با  و اپسیلون ε حداکثر گین (Amax) باند عبور است. اگر Amax در فرکانس برابر با نقطه فرکانس قطع منفی 3 دسی‌بل(fC) تعریف شود،  ε برابر با یک و بنابراین ε۲ نیز یک خواهد بود. با این حال، اگر اکنون می‌خواهید Amax را در یک مقدار افزایش ولتاژ متفاوت به عنوان مثال 1 دسی‌بل  یا 1.1220 (1dB = 20log Amax)  تعریف کنید، پس مقدار جدید اپسیلون ε توسط فرمول زیر به دست می آید:

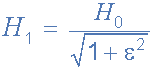
که در این فرمول H۱ حداکثر گین باند عبور و H۰ حداقل گین باند عبور می‌باشند. با جابجایی فرمول داریم:

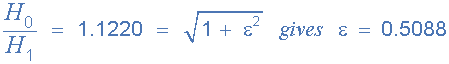
پاسخ فرکانس یک فیلتر را می توان به صورت ریاضی با تابع انتقال آن به کمک تابع انتقال ولتاژ استاندارد H(jω) تعریف کرد:

نکته: می‌توان به جای jω از S استفاده کنیم که در این صورت وارد حوزه لاپلاس خواهیم شد و تابع انتقال برای یک فیلتر پایین‌گذر درجه دوم به این شکل خواهد بود:

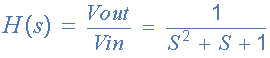
چندجمله‌ای‌های نرمالیزه فیلتر باترورث پایین‌گذر

برای کمک به طراحی این فیلترهای پایین‌گذر، جدول استانداردی از چندجمله‌ای‌های باترورث درجه دوم نرمالیزه پایین‌گذر با استفاده از ضرایب مربوط به فرکانس گوشه ۱ رادیان در ثانیه فراهم شده‌است.

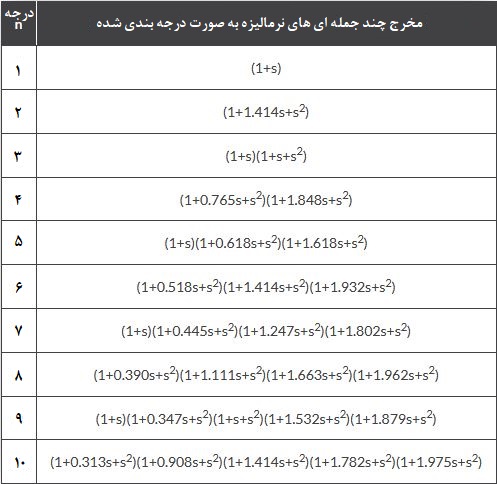۳. چندجمله‌ای‌های نرمالیزه فیلتر باترورث پایین‌گذر

طراحی فیلتر پایین‌گذر باترورث

درجه فیلتر پایین‌گذر اکتیو باترورث را بیابید که مشخصات آن به این صورت است:

حداکثر گین (Amax) نیم دسی‌بل در فرکانس باند عبور (ωp) ۲۰۰ رادیان در ثانیه (۳۱.۸ هرتز)، و حداقل گین منفی۲۰ دسی‌بل در فرکانس باند توقف (ωs) ۸۰۰ رادیان در ثانیه. همچنین یک مدار فیلتر باترورث مناسب برای مطابقت با این الزامات طراحی کنید.

در مرحله اول می‌دانیم حداکثر گین باند عبور Amax = 0.5dB  برابر با گین ولتاژی 0593/1 است، زیرا برای محاسبه گین ولتاژی می‌توان از فرمول dB = 20log(A)  استفاده کرد. بنابراین مقدار اپسیلون ε در فرکانس (ωp) ۲۰۰  رادیان بر ثانیه، توسط فرمول زیر محاسبه می‌شود:

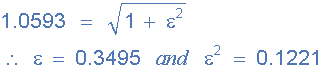
در مرحله بعدی مقدار حداقل گین در باند توقف Amin = -20dB در فرکانس باند توقف (ωs) 800 رادیان بر ثانیه یا 127.3 هرتز برابر است با مقدار 10 (-20dB = 20log(A)).

جایگزین کردن مقادیر در معادله کلی برای پاسخ فرکانسی فیلترهای باترورث، موارد زیر را به ما می دهد:

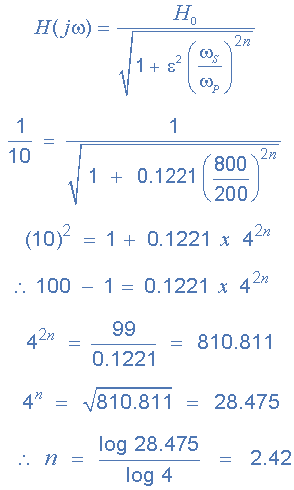
از آنجایی که n باید همیشه یک عدد صحیح (عدد کامل) باشد، پس بالاترین مقدار صحیح بعد از  2.42 عدد 3 است، بنابراین «یک فیلتر درجه سوم مورد نیاز است» و برای تولید یک فیلتر درجه سوم  باترورث، یک طبقه فیلتر درجه دوم کسکود با یک طبقه فیلتر درجه اول مورد نیاز است.

از جدول چندجمله‌ای باترورث نرمالیزه در بالا، مخرج تابع تبدیل فیلتر درجه سوم به صورت (1+s)(1+s+s2) داده می‌شود و این به ما یک بهره A=3-1=2 می‌دهد. چون گین برابر است با  A = 1 + (Rf/R1)، برای مقاومت‌های فیدبک Rf و  R۱ مقادیر 1 کیلواهم با توجه به فرمول (1kΩ/1kΩ) + 1 = 2 به دست می‌آید.

می دانیم که فرکانس گوشه  منفی ۳ دسی بل ω۰ را می‌توان با استفاده از فرمول  1/CRپیدا کرد، اما ما باید ωo  را از فرکانس باند عبور ωp پیدا کنیم پس داریم:

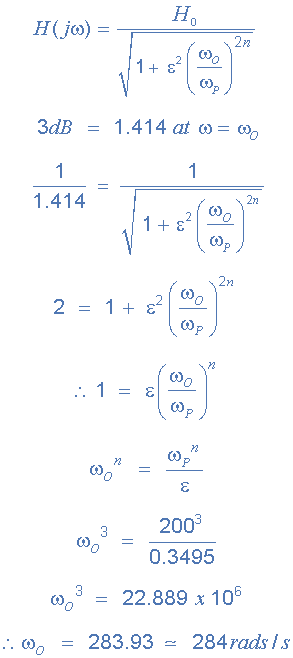
بنابراین، فرکانس گوشه قطع به صورت 284 رادیان بر ثانیه یا 2/45 هرتز، (284/2π) داده می‌شود و با استفاده از فرمول آشنا 1/CR می‌توانیم مقادیر مقاومت‌ها و خازن‌های مدار درجه سوم خود را پیدا کنیم.

با قرار دادن مقدار مقاومت 10 کیلواهم که قبلا محاسبه کردیم مقدار C به دست می‌آید:

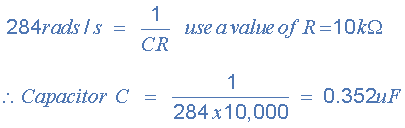
توجه داشته باشید که نزدیک‌ترین مقدار خازن واقعی به عدد بالا برابر با ۳۶/۰ میکروفاراد یا ۳۶۰ نانو فاراد است.

فیلتر پایین گذر باترورث درجه سوم

و در نهایت مدار ما از فیلتر باترورث پایین‌گذر مرتبه سوم با فرکانس گوشه قطع ۲۸۴ رادیان بر ثانیه یا ۲/۴۵ هرتز، حداکثر گین باند عبور ۵/۰ دسی بل و حداقل گین باند توقف منفی ۲۰ دسی‌بل به شرح زیر ساخته شده‌است.

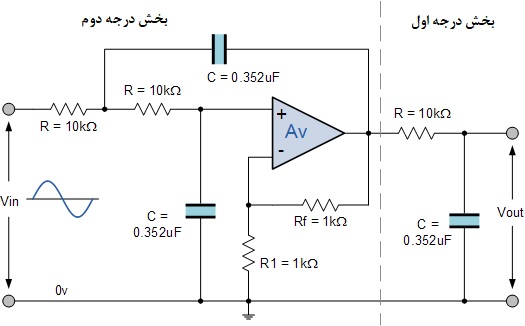۴. فیلتر پایین‌گذر باترورث درجه سوم

پس برای فیلتر پایین‌گذر باترورث درجه سوم با فرکانس گوشه ۲/۴۵ هرتز، مقادیر مقاومت و خازن به ترتیب برابر با ۱۰ کیلواهم و ۳۶۰ نانوفاراد خواهند بود.