راکتانس خازنی

میزان مقاومت جریان عبوری از یک خازن AC را، راکتانس خازنی می‌نامند؛ که با فرکانس منبع تغذیه، رابطه‌ی معکوس دارد.

خازن‌ها،  انرژی را بر روی صفحات رسانای خود به صورت بارالکتریکی ذخیره می‌کنند.  هنگامی‌که یک خازن به یک ولتاژ تغذیه DC متصل می‌شود؛ تا مقدار ولتاژ  اعمال‌شده، با نرخ تعیین شده توسط ثابت زمانی شارژ می‌شود.

تا  زمانی‌که ولتاژ تغذیه وجود دارد؛ یک‌خازن، این‌بار را به طور نامحدود  حفظ‌کرده یا نگه می‌دارد. در طی این فرآیند شارژ، یک‌جریان شارژ (i)، در  خازن جاری شده و در مقابل هرگونه تغییر در ولتاژ، با نرخی که برابر با نرخ  تغییر بارالکتریکی در صفحات خازن است، مخالفت می‌کند. یک خازن، از این‌رو،  با جریان جاری در صفحات آن در مخالفت می‌کند.

رابطه‌ی میان این جریان  شارژ و نرخی را که ولتاژ منبع تغذیه خازن‌ها در آن تغییر می‌کند، می‌توان  از نظر ریاضی به صورت روبرو تعریف نمود:  درجایی‌که، C مقدار ظرفیت خازنی  برحسب فاراد است و dv/dt نرخ تغییر ولتاژ منبع تغذیه در زمان است.  زمانی‌که، “شارژ کامل” رخ داد؛ خازن، جریان جاری از الکترون‌های بیشتر به  صفحات خود را، مسدود می‌نماید، زیرا صفحات اشباع‌شده و خازن، اکنون مانند  یک دستگاه ذخیره موقت عمل می‌نماید.

یک خازن خالص، این‌بار را به طور  نامحدود روی صفحات خود حفظ خواهد نمود؛ حتی اگر ولتاژ منبع تغذیه DC  برداشته شود. با این وجود، در یک مدار ولتاژ سینوسی، که حاوی “ظرفیت AC  “است؛ خازن متناوبا با نرخ تعیین‌شده، توسط فرکانس منبع، شارژ و تخلیه  می‌شود. درنتیجه، خازن‌ها دائما و به‌ترتیب در حال شارژ و تخلیه شدن در  مدارهای AC می‌باشند.

زمانی‌که، یک ولتاژ سینوسی متناوب به صفحات  خازن AC اعمال می‌گردد؛ خازن، ابتدا در یک جهت شارژ می‌شود و سپس در جهت  مخالف، قطبیت خود را با همان نرخ ولتاژ تغذیه AC تغییر می‌دهد. این تغییر  لحظه‌ای در خازن، با این واقعیت در تضاد است که زمان مشخصی برای رسیدن (یا  آزاد‌کردن) بار روی صفحات خازن طول می‌کشد و این رابطه V=Q/C خواهد بود.  مدار زیر را در نظر بگیرید:

ظرفیت AC با منبع سینوسی

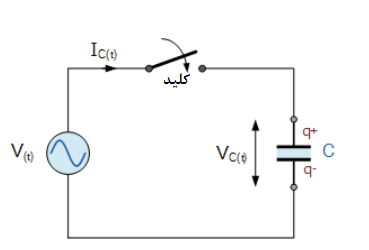1. ظرفیت AC با منبع سینوسی

شکل‌موج سینوسی برای خازن AC

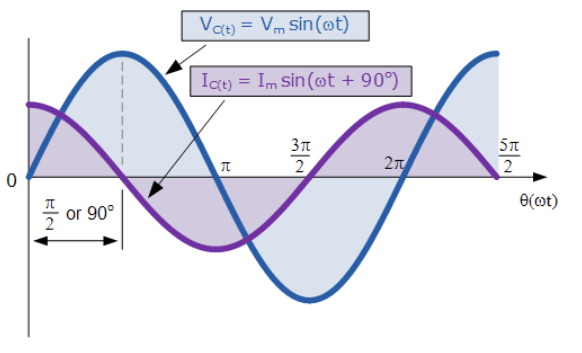2. شکل‌موج سینوسی برای ظرفیت AC

در طول نیم‌ سیکل دوم از °۱۸۰ تا °۳۶۰، ولتاژ منبع  تغذیه، جهت خود را معکوس نموده و به سمت پیک منفی خود که °۲۷۰ است، می‌رود.  در این مرحله، اختلاف پتانسیل بین صفحات، نه کاهش می‌یابد و نه افزایش  می‌یابد و جریان به سمت صفر کاهش می‌یابد. اختلاف پتانسیل دو سرخازن، در  حداکثر مقدار منفی آن است، هیچ جریانی در خازن جاری نیست و به صورت کامل  مانند حالت ۹۰° ،اما در جهت مخالف، شارژ می‌گردد.

در حالی‌که، ولتاژ  منبع تغذیه شروع به افزایش مقدار خود در جهت مثبت تا نقطه ۳۶۰° در خط مرجع  صفر، می‌کند؛ خازن کاملا شارژ شده، باید مقداری از الکترون‌های اضافی خود  را از دست بدهد تا مانند قبل ولتاژ ثابت داشته باشد و در نتیجه، تا  زمانی‌که ولتاژ تغذیه در °۳۶۰ به صفر برسد، شروع به تخلیه کرده و پس از آن  فرآیند شارژ و تخلیه دوباره شروع شود.

از شکل‌موج‌های ولتاژ و جریان و  توضیحات بالا، می‌توان دید که جریان، همیشه به اندازه‌ی 1/4 یک سیکل یا  π/2=90° است؛ “خارج از فاز” بوده و اختلاف پتانسیلی روی دو سر خازن، به  دلیل فرآیند شارژ و تخلیه دارد. پس، رابطه‌ی فاز بین جریان و ولتاژ در یک  مدار خازنی AC، دقیقا معکوس اندوکتانس AC است.

این  اثر را می‌توان، با یک نمودار فازوری در یک مدار خازنی خالص نشان داد که  ولتاژ °۹۰ از جریان، “پیش” تر است و این درحالی است که ولتاژ به عنوان مرجع  در نظر گرفته‌ شود. ما هم‌چنین، می‌توانیم بگوییم که جریان به اندازه ربع  سیکل یا °۹۰، “پیشرو”تر از ولتاژ است که در نمودار زیر نشان داده شده‌ است.

نمودار فازوری برای ظرفیت AC

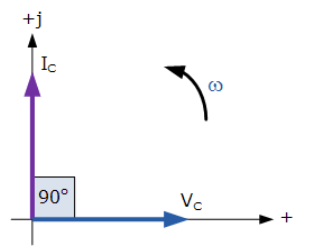3. نمودار فازوری برای ظرفیت AC

بنابراین، برای یک خازن خالص، ، °۹۰ “عقب‌مانده” تر از  خواهد بود یا می‌توان گفت، که ، °۹۰، “پیش‌رو”‌تر از  است.

راه‌های  متفاوت بسیاری، برای به‌خاطرسپردن رابطه فاز میان ولتاژ و جریان جاری، در  یک مدار خازنی خالص وجود دارد؛ اما یکی از روش‌های بسیار ساده و آسان برای  آن، استفاده از اصطلاح حفظی ICE است. ICE مخفف این است که جریان I، اول در خازن AC آمده و نیز C قبل از نیروی محرکه الکتریکی است. به عبارت‌دیگر، جریان قبل از ولتاژ در خازن است که سبب ترتیب I،C و E شده که برابر با ICE است. ولتاژ از هر زاویه‌ی فازی که شروع ‌شود؛ این عبارت، همیشه برای یک مدار خازن AC خالص صادق است.

راکتانس خازنی

بنابراین، اکنون می‌دانیم، که خازن‌ها با تغییر ولتاژ ناشی از  جریان الکترون‌ها، بر روی صفحات خازن، مخالف می‌باشند؛ که مستقیما با نرخ  تغییر ولتاژ در صفحات آن متناسب است در زمانی‌که خازن مداوما شارژ و تخلیه  می‌گردد. برخلاف مقاومت که میزان مخالفت جریان جاری است، مقاومت واقعی آن،  که میزان مخالفت جریان جاری در خازن است، راکتانس خوانده می‌شود.

همانند  مقاومت، راکتانس نیز برحسب اهم است؛ اما از نماد “X” برای آن استفاده  می‌گردد؛ تا از مقدار مقاومت خالص “R” قابل تمایز باشد و از آن‌جایی، که  عنصر مورد بررسی خازن است؛ راکتانس یک خازن، راکتانس خازنی( XC) نامیده می‌شود که بر حسب اهم است.

ازآن‌جایی  که، شارژ و تخلیه‌ی خازن‌ها، متناسب با نرخ تغییر ولتاژ در آن‌هاست؛ هرچه  ولتاژ سریع‌تر تغییر کند؛ جریان بیشتری جاری می‌شود. به همین‌ترتیب، هرچه  ولتاژ کندتر تغییر کند؛ جریان کمتری جاری می‌گردد. این بدین معنی است؛ که  راکتانس خازن AC، رابطه عکس با فرکانس منبع تغذیه دارد که در زیر نشان داده شده است:

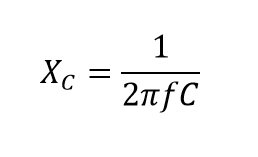
 که:

XC : راکتانس خازنی  برحسب اهم (Ω)

ƒ:  فرکانس برحسب هرتز (Hz)

C: خازن AC برحسب فاراد (F) است.

در هنگام سر و کار داشتن با خازن AC، می‌توانیم راکتانس خازنی را بر حسب رادیان در جایی که ω برابر با ۲πf است؛ تعریف کنیم.

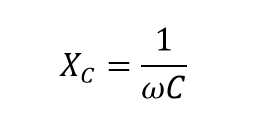
از فرمول فوق، می‌توان دید که مقدار راکتانس خازنی و بنابراین،  امپدانس کلی آن (برحسب اهم)؛ با افزایش فرکانس، مانند یک اتصال کوتاه، به  سمت صفر میل می‌کند. به همین‌ترتیب، با نزدیک‌شدن فرکانس به صفر یا DC،  راکتانس خازن‌ها تا بی‌نهایت، افزایش می‌یابد و مانند یک مدار باز عمل  می‌کند؛ به همین دلیل خازن‌ها، DC را مسدود می‌کنند.

رابطه میان راکتانس خازنی و فرکانس، کاملا معکوس راکتانس القایی (XL)  است که در مقاله قبلی دیدیم. بدین معنی است که راکتانس خازنی، با فرکانس،  “رابطه عکس” دارد و در فرکانس‌های پایین، مقدار زیاد و در فرکانس‌های  بالاتر، مقدار کمی دارد.

راکتانس خازنی و فرکانس

راکتانس خازنی یک خازن، با افزایش فرکانس درصفحات آن کاهش  می‌یابد؛ بنابراین، راکتانس خازنی معکوسا متناسب با فرکانس است. راکتانس  خازنی با جریان جاری مخالفت می‌کند؛ اما بار الکترواستاتیک صفحات(مقدار  خازن AC ) ثابت می‌ماند.

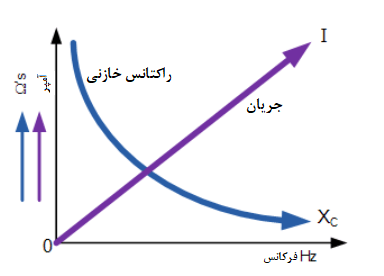۴. اثر فرکانس بر راکتانس خازنی

این بدان معنی است؛ که خازن راحت‌ تر می‌تواند، در هر نیم سیکل،  تغییر بار صفحات خود را کاملا جذب کند. هم‌چنین، با افزایش فرکانس، جریان  جاری در خازن از نظر مقدار، افزایش می‌یابد؛ زیرا نرخ تغییر ولتاژ در صفحات  آن افزایش می‌یابد.

می‌توان، اثر فرکانس‌های بسیار کم و بسیار زیاد را بر راکتانس یک ظرفیت AC خالص به شرح زیر ارائه داد:

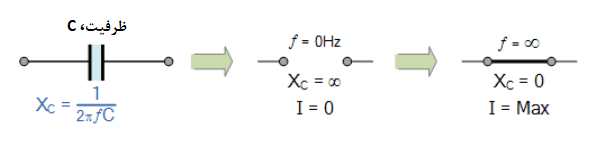۵. اثر فرکانس خیلی کم و خیلی زیاد بر راکتانس خازنی

در یک مدار AC حاوی خازن خالص، جریان (جریان الکترون) که در خازن جاری است؛ به صورت زیر است:

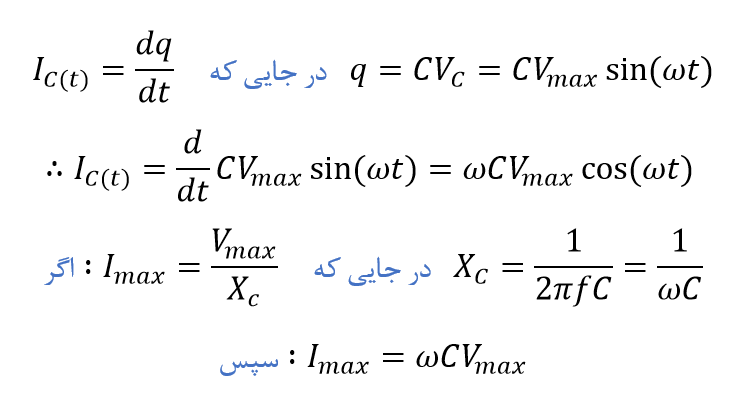
بنابراین، جریان rms جاری در یک خازن AC، به صورت زیر تعریف می‌شود:

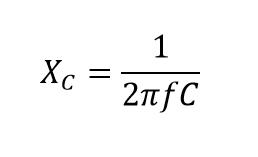
در این‌جا، IC = V/(1/ωC) (یا IC = V/XC) است؛ که دامنه جریان می‌باشد و اختلاف فاز یا زاویه فاز میان شکل‌ موج‌های جریان و ولتاژ، برابر با θ = + ۹۰o  است. برای یک مدار خازنی خالص، Ic با زاویه 90° ازVc پیش‌تر است یا Vc با زاویه 90° از Ic عقب تر است.

 حوزه‌ی فازور

در حوزه فازور، ولتاژ روی صفحات یک خازن AC خواهد بود:

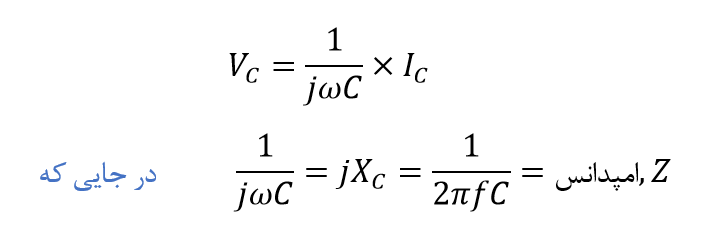
و فرم قطبی را می‌توان نوشت:  XC ∠ -۹۰o که:

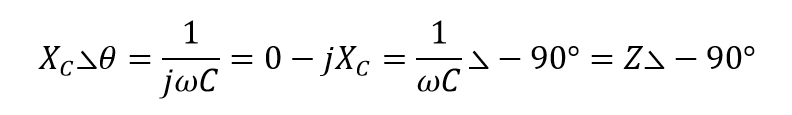
RC سری در مدار AC

در بالا مشاهده شد؛ که جریان جاری در یک خازن AC خالص، از ولتاژ ° 90جلوتر خواهد بود، اما در دنیای واقعی، امکان داشتن یک خازن AC خالص، وجود ندارد؛ زیرا همه‌ی خازن‌ها با داشتن مقاومت داخلی در سطح صفحات خود، باعث ایجاد جریان نشتی می‌شوند.

در  نتیجه، می‌توانیم در نظر بگیریم، که خازن ما، اگر دارای مقاومت باشد، یک  مقاومت (R) سری با خازن (C) خواهد بود که می‌توان آن را “خازن ناخالص”  نامید.

اگر خازن، دارای مقداری مقاومت “داخلی” باشد؛ ما باید امپدانس کلی خازن را، به صورت یک مقاومت سری با یک خازن در یک مدار AC، که هم حاوی  ظرفیت (C) و هم مقاومت (R) است؛ نشان دهیم. V در کل ترکیب، مجموع فازور دو مولفه ولتاژ VR و VC  است.

این  بدین معناست، که جریان عبوری از خازن، هم‌چنان از ولتاژ جلوتر است؛ اما  بسته به مقادیر C و R  و در واقع مجموع فازور، مقدار آن از 90° کمتر خواهد  بود که زاویه‌ی مربوطه بین آن‌ها با نماد یونانی phi(φ) نشان داده می‌شود.

مدار سری RC را در نظر بگیرید؛ در جایی‌که، مقاومت اهمی (R) به صورت سری به خازن خالص (C) متصل شده‌است.

مدار سری مقاومتی-خازنی

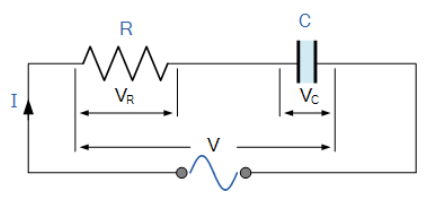۷. مدار  مقاومتی-خازنی سری

در مدار سری RC بالا، می‌توان دید که جریان جاری در مدار، بین مقاومت و خازن مشترک است؛ در حالی‌که ولتاژ از دو مولفه VR و VC ساخته می‌شود. ولتاژ حاصل از این دو جز را می‌توان به صورت ریاضیاتی یافت اما از آنجایی‌که، بردارهای VR و VC ،۹۰° خارج از فاز می‌باشند؛ با ساختن نمودار برداری، می‌توان آن‌ها را به صورت برداری اضافه نمود.

 برای  ایجاد نمودار برداری برای خازن AC ،باید یک مولفه‌ی مشترک یا مرجع  یافت‌شود و در یک مدار AC سری، جریان مشترک بوده و می‌تواند به عنوان منبع  مرجع استفاده‌شود؛ زیرا این جریان هم در مقاومت و هم در خازن جاری است.  نمودارهای برداری منفرد برای یک مقاومت خالص و یک خازن خالص به صورت زیر  است:

نمودارهای برداری برای خازن و مقاومت خالص

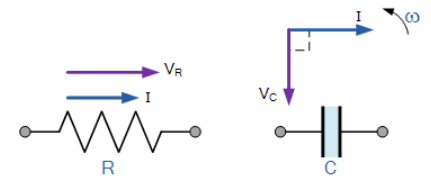۸. نمودارهای برداری برای دو عنصر خالص

هر دو بردار ولتاژ و جریان برای مقاومت AC هم‌فاز بوده و از این رو از نظر مقیاس‌گذاری، بردار ولتاژ VR ،بر بردار جریان IR سوار می‌شود. هم‌چنین از بالا متوجه شدیم که جریان در یک مدار خازنی AC خالص (ICE) از ولتاژ جلوتر است؛ از این‌رو، بردار VC، 90° عقب تر از بردار جریان می‌باشد،که در یک مقیاس و راستا با VR رسم شده‌است.

نمودار برداری ولتاژ حاصل

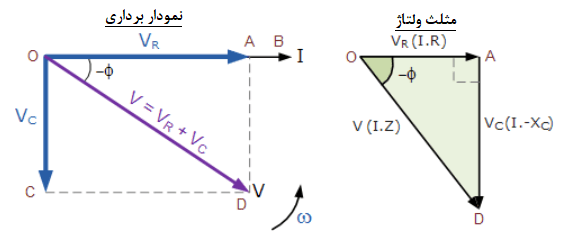۹. نمودار برداری ولتاژ حاصل

در نمودار برداری بالا ؛ خط OB مرجع جریان افقی بوده و خط OA  ولتاژ دوسر مولفه‌ی مقاومتی است که هم‌فاز با جریان است. خط OC ولتاژ خازنی  را نشان می‌دهد؛ که °90 از جریان عقب‌تر و بنابراین می‌توان دریافت که  جریان ،از ولتاژ خازنی خالص، °90 جلوتراست. خط OD ولتاژ تغذیه حاصل را به  ما می‌دهد.

از آن‌جایی که جریان، °90 از ولتاژ در خازن خالص جلوتر است؛ نمودار فازوری حاصل از یک ولتاژ منفرد به دو مولفه VR و VC تقسیم می‌شود؛ که نشان‌دهنده‌ی یک مثلث قائم الزاویه است؛ که در بالا با  نماد OAD نشان داده شده‌است. پس می‌توانیم از قضیه فیثاغورث استفاده نماییم  تا مقدار ولتاژ حاصل از مدار مقاومت/ خازن (RC) را به صورت ریاضی پیدا  کنیم.

از آنجایی‌که VR = I.R و VC = I.XC است؛ ولتاژ اعمال‌شده، مجموع این دو بردار به شرح زیر خواهد بود:

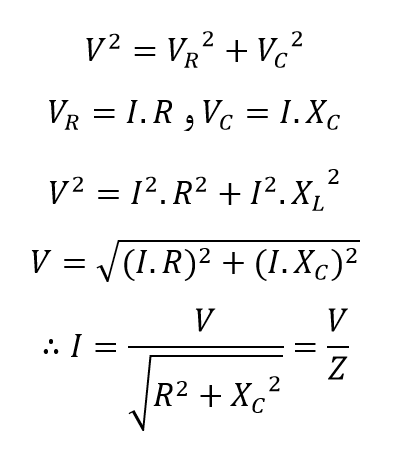
اندازه  نشان‌دهنده‌ی امپدانس Z در یک مدار است.

امپدانس خازن

امپدانس Z، که  برحسب اهم (Ω) است، میزان مقاومت “کامل” جریان جاری در یک مدار AC است؛که  از مقاومت (بخش حقیقی) و راکتانس (بخش موهومی) تشکیل شده‌ است.

یک امپدانس مقاومتی خالص دارای زاویه‌ی فاز ° ۰ بوده، در حالی‌که یک امپدانس خازنی خالص دارای زاویه فاز °۹۰- می‌باشد.

با  این وجود، زمانی‌که مقاومت‌ها و خازن‌ها در یک مدار به‌یک‌دیگر اتصال  می‌یابند؛ بسته به عناصر مورد استفاده، امپدانس کل دارای زاویه‌ی فازی بین 0  تا  90° است.سپس با استفاده از مثلث امپدانس می‌توان امپدانس مدار RC ساده  را به صورت زیر به دست‌آورد:

مثلث امپدانس RC

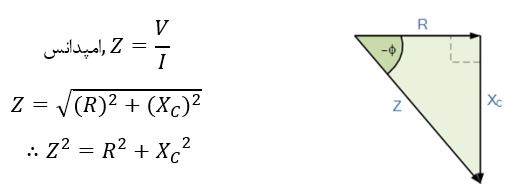
در نتیجه :

که j، نشان‌دهنده‌ی ° 90 شیفت فاز است.

این، بدین معنی است، که با استفاده از قضیه‌ی فیثاغورث، زاویه فاز منفی (θ) بین ولتاژ و جریان به صورت زیر خواهد بود:

زاویه فاز

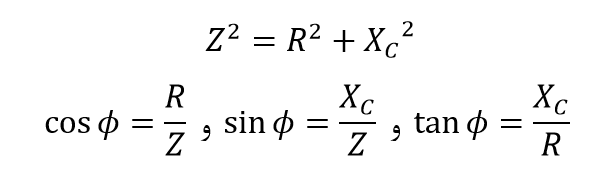
مثال شماره 1 -   ظرفیت AC

یک ولتاژ منبع تغذیه سینوسی تک‌فاز، این‌گونه تعریف می‌شود: V(t) = 240 sin(314t – 20o) که به یک خازن خالص AC ،200uf متصل شده‌است. مقدار جریان جاری در خازن را تعیین کرده و نمودار فازوری حاصل را رسم کنید.

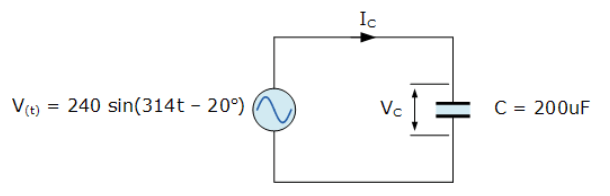10. خازن AC - مثال 1

ولتاژ دو سر خازن، همان ولتاژ تغذیه خواهد بود. تبدیل این مقدار در حوزه زمان به فرم قطبی به ما می‌دهد:VC = ۲۴۰ ∠-۲۰o (v). راکتانس خازنی نیز برابر با XC = 1/( ω.200uF ) خواهد بود. در نتیجه، جریان عبوری از خازن که توسط قانون اهم محاسبه می‌شود، خواهد بود:

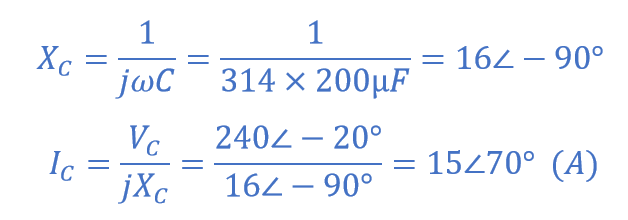
با °۹۰ پیش تر بودن جریان از ولتاژ، نمودار فازوری خواهد بود:

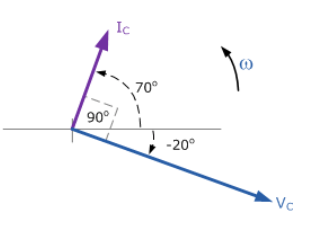۱۱. نمودار فازوری - مثال ۱

مثال شماره 2 - ظرفیت AC

یک خازن که دارای مقاومت داخلی 10Ω و مقدار ظرفیت  100uFاست؛ به یک منبع تغذیه به صورت روبرو متصل شده است: V(t) = 100 sin (314t) مقدار پیک جریان جاری در خازن را بیاید. هم‌چنین یک مثلث ولتاژ بسازید که افت ولتاژ منفرد را نشان دهد.

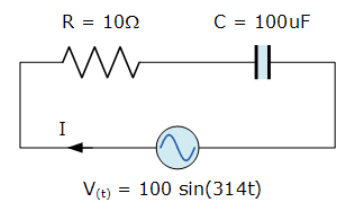12. مثال شماره 2 - خازن و مقاومت  سری در مدار AC

راکتانس خازنی و امپدانس مدار به‌صورت زیر محاسبه می‌گردد:

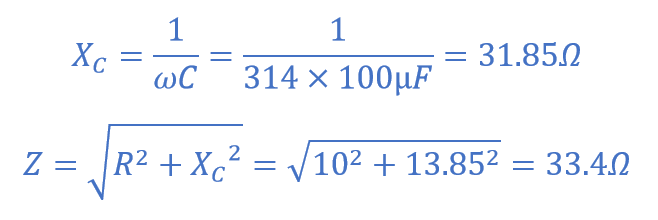
سپس جریان جاری در خازن و مدار، به صورت زیر بدست می آید:

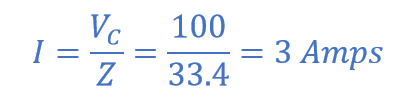
زاویه‌ی فاز بین جریان و ولتاژ از مثلث امپدانس بالا، به صورت زیر محاسبه می‌شود:

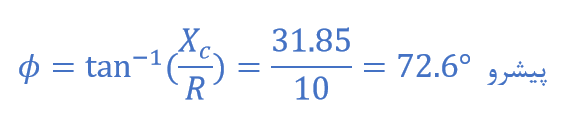
سپس افت هر ولتاژ منفرد در مدار به صورت زیر خواهد بود:

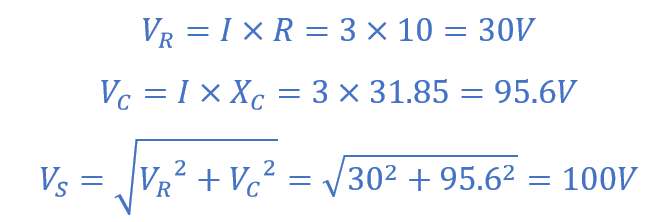
درنهایت، مثلث ولتاژ حاصل برای مقادیر پیک محاسبه شده، خواهد بود:

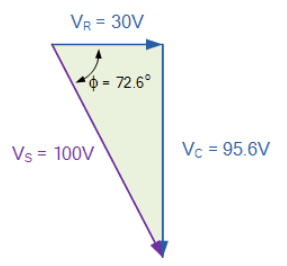۱۳. مثلث ولتاژ -مثال ۲

خلاصه ظرفیت AC

در یک مدار خازنی  AC خالص،  ولتاژ و جریان هر دو “خارج فاز” می‌باشند؛ در حالی‌که، جریان °90 از ولتاژ  پیشروتر است. و ما می‌توانیم، این را با استفاده از ترکیب “ICE” بخاطر  بسپاریم. مقدار مقاومت AC خازنی، را امپدانس Z) می‌نامند که توسط مقدار راکتیو یک خازن که “راکتانس خازنی”(XC) نامیده می‌شود به فرکانس مربوط می‌گردد. در یک مدار خازنی AC، مقدار راکتانس خازنی برابر ( 2πƒC )/1 یا ( jωC )/1 است.

تاکنون،  مشاهده کردیم که رابطه میان ولتاژ و جریان یکسان نیست و تغییر در هر سه  عنصر پسیو خالص خواهد بود. در یک مقاومت، زاویه فاز برابر با °۰، در یک  اندوکتانس برابر با °۹۰، در حالی‌که در یک خازن برابر با °۹۰- است.

در  مقاله بعدی، در مورد مدارهای سری RLC، به رابطه‌ی ولتاژ – جریان هر سه  عنصر پسیو (غیرفعال) هنگامی که به یک دیگر در یک مدار سری متصل شده‌اند، و  زمانی‌که شکل‌ موج سینوسی AC حالت مانا همراه با نمایش نمودار فازوری  مربوطه آن است؛ خواهیم پرداخت.