امپدانس و امپدانس مختلط

در یک مدار جریان متناوب، که معمولا به‌عنوان “مدار AC” شناخته می‌شود؛ امپدانس مخالفت کننده با جریان جاری در مدار است. امپدانس، مقداری بر حسب اهم است  که اثر ترکیبی عناصر محدودکننده جریان در مدار مانند رزیستانس (R)،  اندوکتانس (L) و ظرفیت خازنی (C) است.

در یک مدار مستقیم یا مدار DC،  به مخالفت کننده با جریان جاری رزیستانس می‌گویند؛ اما در یک مدار AC،  امپدانس نتیجه هر دو عناصر مقاومتی (R) و راکتیو (X) مدار است. در حالی که  مقدار مقاومت الکتریکی موجود در یک مدار DC با حرف “R” نشان داده می‌شود؛  اما برای یک مدار متناوب AC ، حرف یا نماد “Z” برای نشان دادن مخالفت با  جریان جاری استفاده می‌گردد.

همچنین، مانند رزیستانس DC، امپدانس  برحسب اهم توصیف می‌شود و در صورت لزوم از مضرب‌های اهم استفاده می‌گردد.  برای مثال، میکرواهم (uΩ  یا 10-۶)، میلی‌اهم (mΩ  یا 10-۳)، کیلواهم (kΩ  یا 10۳) و مگااهم (MΩ  یا 10۶) و… . و برای هر مورد، امپدانس براساس قانون اهم مانند زیر تعریف می‌شود:

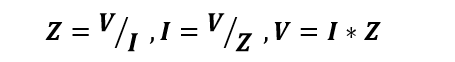
در جاییکه، Z، امپدانس با یکای اهم، V با یکای ولت و I با یکای آمپر است.

فرم امپدانس

قبلا گفتیم که امپدانس (Z) اثر ترکیبی از مقادیر کل رزیستانس (R)  و راکتانس (X) موجود در یک مدار AC است. اما امپدانس، به فرکانس نیز  وابسته است و بنابراین دارای زاویه فاز مرتبط با آن است. زاویه فاز  راکتانس، چه القایی و چه خازنی، 90° دارای اختلاف فاز با عنصر مقاومتی است.  پس، مقادیر مقاومتی و راکتیو مدارها، نمی‌توانند به سادگی با هم جمع شوند  تا مقدار امپدانس کل مدارها به‌دست بیاید و R+X برابر با Z نیست.

در  اینجا شایان ذکر است که مقاومت‌ها مقدار خود را با فرکانس تغییر نمی‌دهند و  بنابراین راکتانسی ندارند (شامل سیم‌های حلقه‌ای نمی‌شوند)؛ بنابراین  رزیستانس آن‌ها، مستقیما برابر با امپدانس آن‌هاست (R=Z). درنتیجه،  مقاومت‌ها زاویه فاز ندارند و ولتاژ دو سر آن‌ها، “هم‌فاز” با جریان است.

درهرحال، راکتانس، چه به شکل راکتانس القایی (XL) چه به شکل راکتانس خازنی (XC)،  با فرکانس تغییر می‌کند و سبب می‌شود مقدار امپدانس مدار با تغییر فرکانس  منبع‌تغذیه، تغییر یابد. به‌همین دلیل است که گاهی اوقات از عبارات  “امپدانس مقاومتی” (برای مقاومت‌ها) و “امپدانس راکتیو” (برای سلف‌ها و  خازن‌ها) در تجزیه و‌ تحلیل مدارهای AC استفاده می‌شود.

ازآن‌جایی‌که،  نمی‌توان مقادیر مقاومتی و راکتیو مدارها را برای یافتن امپدانس‌کل (Z) به  هم اضافه کرد؛ زیرا 90° با یکدیگر اختلاف فاز دارند و عمود بر هم  می‌باشند. می‌توانیم این مقادیر را بر یک نمودار دو بعدی رسم کنیم که محور  x، مقاومتی یا “محورحقیقی” بوده و محور y، راکتیو یا “محورموهومی” است. این  همان روشی است؛ که در ساخت مثلث قائم‌الزاویه به کار می‌رود.

نمودارهای  قائم‌الزاویه زیر  چگونگی ترکیب رزیستانس و راکتانس برای تشکیل امپدانس را  نشان می‌دهند. امپدانس وتر (طویل‌ترین ضلع) مثلث امپدانس مختلط مدار است.

رزیستانس و راکتانس القایی

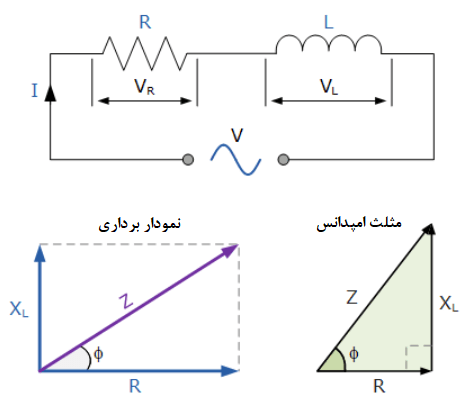
همانطور که در مثلث سه ضلعی قائم‌الزاویه مشاهده می‌شود؛  می‌توانیم با استفاده از قضیه فیثاغورث و معادلات مربوط به آن، دوضلع مثلث  قائم‌الزاویه ،که نماینده رزیستانس و راکتانس می‌باشند، را نشان‌دهیم. از  طریق آن‌ها اندازه وتر مشخص می‌گردد .در این قضیه، امپدانس، راکتانس و  رزیستانس به‌صورت زیر تعریف می‌شود:

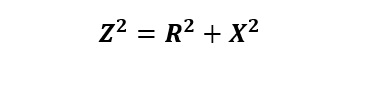
داریم:

به این ترتیب، می‌توانیم نشان دهیم که بردار امپدانس (Z)، حاصل  جمع برداریِ بردار رزیستانس (R) و بردار راکتانس (X) بوده و دارای شیب مثبت  است؛ همانطور که در زیر آمده‌:

امپدانس مدار RL

زاویه فاز (φ)، زاویه بین بردار امپدانس و بردار رزیستانس برحسب درجه، به صورت زیر بیان می‌شود:

زاویه‌فاز مدار RL

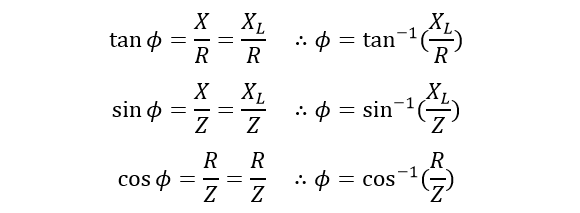
همانند مدار قبلی شامل سلف و راکتانس القایی، می‌توانیم امپدانس  مختلط یک مدار AC، شامل خازن‌ها و راکتانس خازنی را نیز نشان دهیم. همان  مثلث قائم‌الزاویه قبلی، برای نشان دادن چگونگی ترکیب رزیستانس و راکتانس  خازنی، برای نمایش وتر(طویل‌ترین ضلع) مثلث که نشان‌دهنده‌ی امپدانس مختلط  مدار است؛ به‌کار برده می‌شود.

به‌یاد داشته باشید؛ که برای یک خازن،  بردار امپدانس (Z)، مجموع برداری، بردار رزیستانس (R) و بردار راکتانس (X)  با جهتی مخالف جهت بردار XL  قبلی بوده و با شیب منفی کشیده‌ می‌شود. این امر نشان میدهد؛ که اثر راکتانس خازنی در مدار AC، عکس راکتانس القایی است.

رزیستانس و راکتانس خازنی

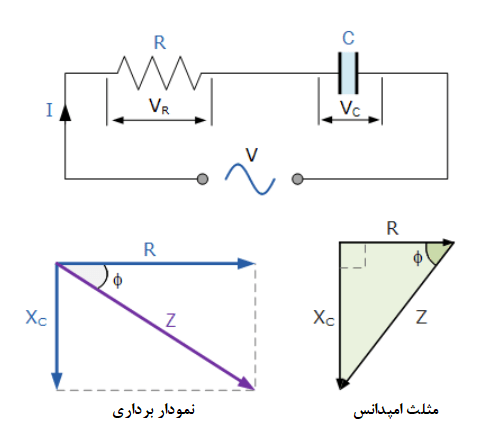
همانند قبل، می‌توانیم با استفاده از قضیه فیثاغورث و معادلات  مربوط به آن، دوضلع مثلث قائم‌الزاویه که نماینده رزیستانس و راکتانس خازنی  می‌باشند؛ نشان داده و از طریق‌آنها، اندازه وتر را که امپدانس مختلط است؛  به‌دست آورد.در این قضیه، امپدانس، راکتانس و رزیستانس به‌صورت زیر تعریف  می‌شود:

امپدانس مدار RC

تانژانت زاویه فاز (φ)، زاویه بین بردار امپدانس و بردار  رزیستانس را تعریف می‌کند. تانژانت زاویه فاز، برابر با تقسیم راکتانس ‌بر  رزیستانس به‌صورت زیر است:

زاویه فاز مدار RC

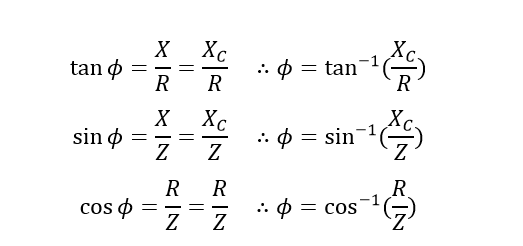
بنابراین از نمودارهای برداری بالا، می‌توان برای نمایش ترکیب  رزیستانس و راکتانس (القایی و خازنی) با یکدیگر، برای شکل دادن امپدانس  استفاده نمود. همچنین می‌توان از مقادیر اهمی مدار، مانند Z ،R و X برای  یافتن زاویه فاز φ بین ولتاژ منبع VS و جریان مدار I استفاده نمود.

مثال ۱

یک سلف 53mH و مقاومت 15Ω به‌صورت سری به‌هم متصل شده‌اند. امپدانس کل و زاویه‌فاز را برای منبع 60Hz محاسبه نمایید.

1. امپدانس کل مدار Z

۲. زاویه فاز φ

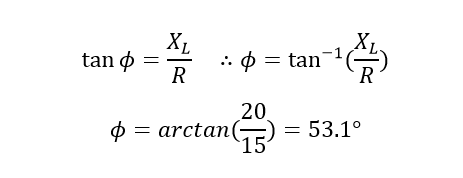
مثال ۲

یک کویل سلونوئیدی هنگام اتصال به مولتی‌متر، دارای مقاومت ثابت  12Ω است. اگر کویل سلونوئید هنگام اتصال به منبع‌تغذیه 100V,1000Hz، 5آمپر  جریان بکشد، اندوکتانس کویل و ضریب‌توان را محاسبه کنید.

1. اندوکتانس کویل XL

۲. ضریب توان

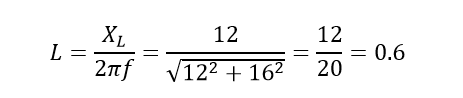
دیدیم که امپدانس (Z)، اثر ترکیبی رزیستانس (R)  و راکتانس (X) در یک مدار AC است و برای یک عنصر کاملا راکتیو X، دارای  90°  اختلاف‌فاز با عنصر مقاومتی است؛ که برای اندوکتانس (+90°) و برای  ظرفیت‌خازنی (-90°) است.

اما اگر مدار سری AC، دارای هر دو راکتانس القایی XL و راکتانس خازنی XC باشد؛ چگونه‌ بر امپدانس مختلط مدار اثر خواهد داشت؟

امپدانس مدار RLC

راکتانس، راکتانس است! با وجود اینکه، مثلث امپدانس یک سلف،  دارای شیب مثبت و مثلث امپدانس یک خازن دارای شیب منفی است؛ جمع ریاضیاتی  دو امپدانس، مقدار کلی امپدانس مدار را تولید خواهدکرد. ترکیب راکتانس مدار  سری، مجموع راکتانس القایی XL و راکتانس خازنی XC خواهد بود که در زیر آمده است:

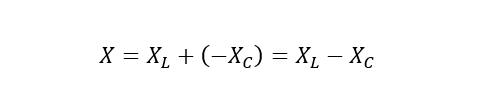
و امپدانس را به ما خواهد داد:

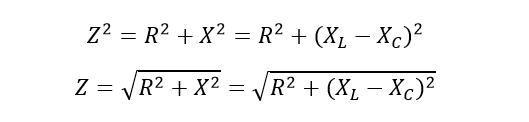
براساس قانون کلی دست راست، مقدار بزرگتر راکتانس را از مقدار کوچکتر آن کم خواهیم کرد؛ اما چه XL بزرگتر باشد و چه XC، تفاوتی نخواهد داشت، زیرا مربع یک مقدار منفی همیشه در ریاضیات مثبت خواهد بود. مانند ۲(-۲) که برابر با حاصل ۲۲  و یا 4 است. پس صحیح است، که از یکی از تفریق‌های (XL-XC) یا  (XC-XL) برای یافتن مقدار راکتانس ترکیبی، قبل از افزودن آن به مقدار رزیستانس استفاده کنیم.

مثلث امپدانس نتیجه به‌صورت زیر خواهد بود:

مثلث امپدانس RLC

مثلث امپدانس RLC

شیب مثبت یا منفی امپدانس، از لحاظ جهت، وابسته به این‌است؛ که کدام امپدانس القایی(XL-XC) یا خازنی (XC-XL) بزرگتر باشد. پس امپدانس مختلط مدار به‌شکل Z = R ±jΧ تعریف می‌شود.

روشن است که اگر مدار AC تنها شامل اندوکتانس یا ظرفیت خازنی باشد؛ امپدانس برابر با Z = XL-XC یا برعکس خواهد بود. اما اگر مدار در حالت تشدید باشد؛ راکتانس خالص برابر با صفر Z=0 می‌شود. زیرا به‌دلیل XL=XC ، راکتانس القایی برابر و مخالف مقدار راکتانس خازنی است. و به‌همین دلیل  است که جریان جاری در مدار، تنها توسط یک مقاومت دینامیک (R) در حالت  تشدید، محدود می‌شود.

مثال ۳

یک مقاومت غیرالقایی 10Ω، یک خازن 100uF و یک سلف 0.15H به صورت  سری به یک منبع تغذیه 240V,50Hz متصل شده‌است. راکتانس القایی، راکتانس  خازنی، امپدانس مختلط‌ مدار و ضریب توان را محاسبه نمایید.

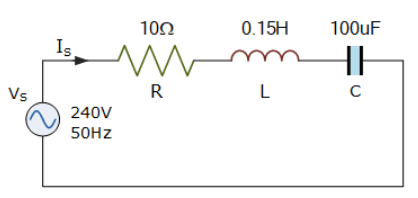
R = R = 10Ω

1. راکتانس القایی XL

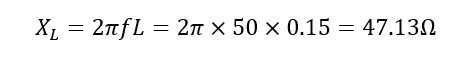
۲. راکتانس خازنی XC

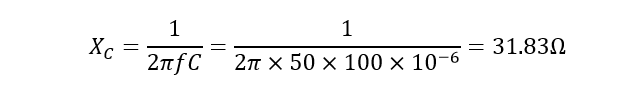
۳. امپدانس مختلط Z

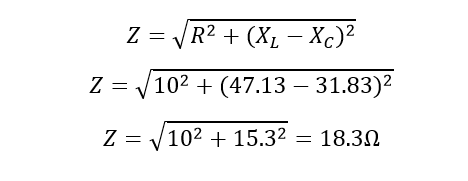
۴. ضریب توان

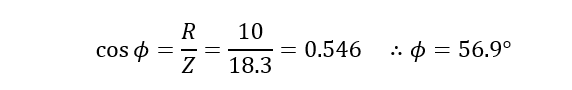
دراین آموزش دیدیم که امپدانس Z، مخالفت کننده با جریان جاری در  یک مدار AC و اثر ترکیبی رزیستانس و راکتانس است. همچنین دیدیم که امپدانس  با مجموع ریاضیاتی برابر نبوده، بلکه برابر با مجموع برداری عناصر مقاومتی و  راکتیوی در مدار است و دارای 90° “اختلاف‌فاز” با عنصر مقاومتی می‌باشد.

امپدانس مختلط در یک ترتیب سری بر اساس قانون اهم و برای یک مدار کاملا راکتیوی خواهد بود:

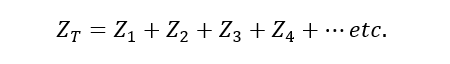
اما در مدارهای موازی، محاسبه امپدانس چگونه خواهد شد؟

امپدانس های موازی

اگر یک رزیستانس منفرد و یک راکتانس منفرد، به صورت موازی  به‌یکدیگر متصل شوند؛ امپدانس هر شاخه موازی را باید پیدا نمود. اما از آن  جایی که تنها دو عنصر R و X، به‌صورت موازی به‌هم متصل شده‌اند؛ می‌توان از  معادله استاندارد دو رزیستانس موازی برای به دست آوردن حاصل، استفاده  نمود:

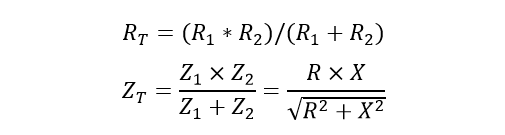
 Z ،R و X همه برحسب اهم می‌باشند.

باید توجه داشت که  هنگام سروکار داشتن با منبع و فرکانس‌های AC، چون عنصر مقاومتی دارای 90°  اختلاف فاز با عنصر راکتیوی است؛ حاصل با جمع برداری X و R به‌دست می‌آید.

اگر  “n” شاخه، حاوی امپدانس‌های مختلط به‌صورت موازی به هم متصل شده‌باشند؛  امپدانس کل، مجموع برداری همه شاخه‌های موازی است. بنابراین معکوس امپدانس  کل به صورت زیر است:

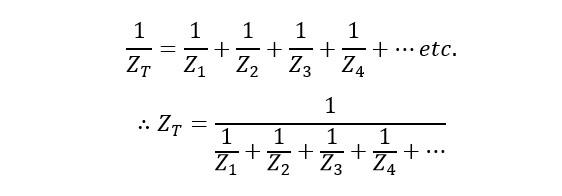
و خواهیم داشت:

رزیستانس و اندوکتانس موازی

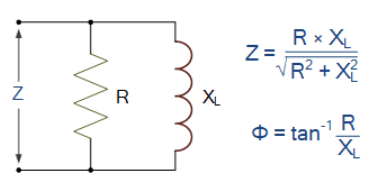رزیستانس و اندوکتانس موازی

رزیستانس و ظرفیت خازنی موازی

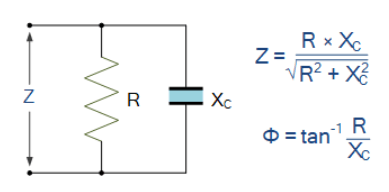رزیستانس و ظرفیت خازنی موازی

رزیستانس، اندوکتانس و ظرفیت خازنی موازی

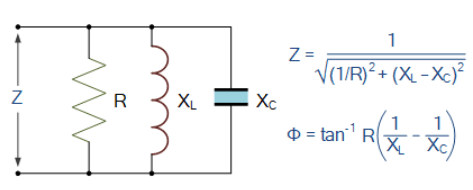رزیستانس، اندوکتانس و ظرفیت خازنی موازی

برای یک مدار موازی RLC، توجه داشته‌باشید که در فرکانس تشدید XL=XC بوده و امپدانس صفر است و تنها رزیستانس موجود در مدار، R خواهد بود. از  این‌رو، تنها هنگام تشدید، امپدانس دینامیکی مدار به‌صورت Z=R تعریف  می‌شود.