گیت منطقی XNOR

تابع گیت XNOR یا Exclusive-NOR (NOR حذفی)، یک گیت منطقی دیجیتال است؛ که معکوس یا مکمل شکل تابع گیت XOR (OR حذفی)، می‌باشد.

اساسا گیت XNOR، ترکیبی از گیت XOR و گیت NOT می‌باشد؛ اما دارای یک جدول درستی مشابه به گیت NOR استاندارد است؛ که در آن خروجی به‌صورت نرمال در سطح منطقی “1” قرار دارد و تنها زمانی به “LOW” و سطح خروجی “1” می‌رود؛ که یکی از ورودی‌های آن در سطح منطق “1” باشند.

با این‌حال، خروجی منطقی “۱”  تنها، درصورتی بدست‌ می‌آید؛ که هردوی (Both) این ورودی‌ها در سطح منطقی برابر، یعنی هردو “۱” یا هردو “۰” باشند. برای مثال “۰۰” و “۱۱” باشند. این ترکیب ورودی، عبارت بولی زیر را به ما می‌دهد.

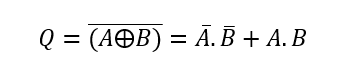
خروجی گیت منطقی دیجیتال XNOR، تنها زمانی به “HIGH” می‌رود؛ که پایانه‌های دو ورودی آن، A و B، در سطح منطقی “یکسان“ باشند؛ یعنی می‌توانند یا در سطح منطقی “۱” و یا سطح منطقی “۰” باشند. به بیان دیگر، تعداد زوج از منطق “۱” در ورودی‌ها، خروجی در منطق “۱” را نتیجه می‌دهد؛ در غیر این‌صورت، خروجی در سطح منطقی “۰” خواهد بود.

پس این نوع از گیت، زمانی دارای خروجی “۱” است؛ که ورودی‌های آن “منطقا برابر“ یا “معادل“ هم باشند و این دلیلی است؛ که گاهی گیت XNOR، گیت هم‌ارز نامیده می‌شود.

نماد منطقی برای گیت XNOR، به‌سادگی همان نماد گیت XOR است؛ که یک دایره یا “حباب وارون‌ساز”(O) به نشانه‌ی تابع NOT در خروجی آن، قرار گرفته‌است. پس گیت Exclusive-NOR، وارون یا “مکمل“ شکل گیت XOR(A⨁B) است؛ که پیش از این دیدیم.

معادل گیت XNOR

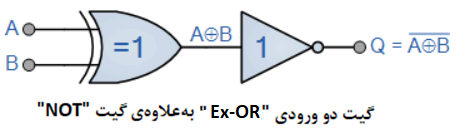
Exclusive-NOR، که به‌صورت تابع “Ex-NOR” یا “XNOR” نیز نوشته می‌شود؛ با ترکیب گیت‌های استاندارد با یکدیگر، برای شکل‌دهی تابع‌های گیت پیچیده‌تر بدست می‌آید و مثالی از یک Exclusive-OR با دو ورودی، در زیر آورده شده‌است.

گیت منطقی دیجیتال Exclusive-NOR

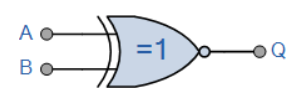
گیت منطقی XNOR با دو ورودی

جدول درستی

اگر B و A برابر باشند به ما خروجی Q را می‌دهد

نماد

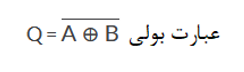
این گیت دو ورودی، عبارت بولی زیر را در اختیار ما قرار دهد:

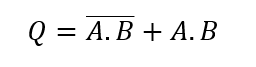
تابع منطقی پیاده‌سازی‌شده توسط گیت دو ورودی XNOR ، ” زمانی‌که، A و B  برابر باشند”، خروجی Q را در اختیار ما می‌گذارد. درحالت کلی، گیت XNOR خروجی در منطق “1” را تنها زمانی خواهد داشت؛ که تعداد زوجی از “1” در ورودی‌های گیت باشند (معکوس گیت Ex-OR)؛ به جز زمانی‌که تمام ورودی‌ها در حالت “LOW” هستند.

پس یک تابع Ex-NOR با بیش از دو ورودی، یک “تابع زوج” یا پیمانه‌ی دو جمع (Mod-2-SUM) و نه XNOR نامیده می‌شود. این توضیح را می‌توان گسترش داد؛ تا هر تعدادی از ورودی‌های جداگانه‌ را همانند زیر به یک گیت Exclusive-NOR سه ورودی، اعمال کرد.

گیت منطقی XNOR با سه ورودی

جدول درستی

هر تعداد زوجی از ورودی‌ها، خروجی Q را به ما می‌دهد

نماد

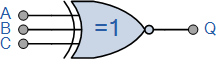
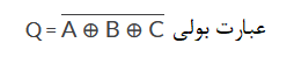
این گیت سه ورودی، عبارت بولی زیر را در اختیار ما قرار دهد:

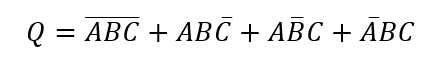
پیش از این گفتیم؛ که تابع Ex-NOR، از ترکیب گیت‌های منطقی پایه‌ی مختلف Ex-OR و گیت NOT بدست می‌آید و با استفاده از جدول درستی دو ورودی در بالا، تابع XNOR را به  گسترش می‌دهیم؛ که به این معناست؛ که بیان جدیدی را می‌توانیم با استفاده از گیت‌های منحصربفرد زیر، درک کنیم.

مدار معادل گیت XNOR

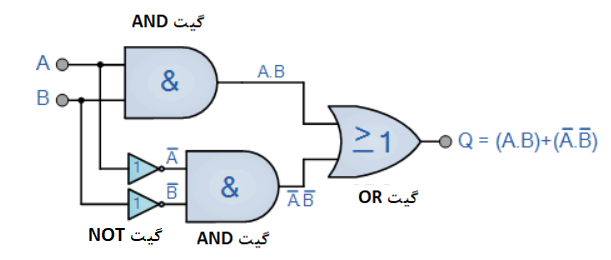
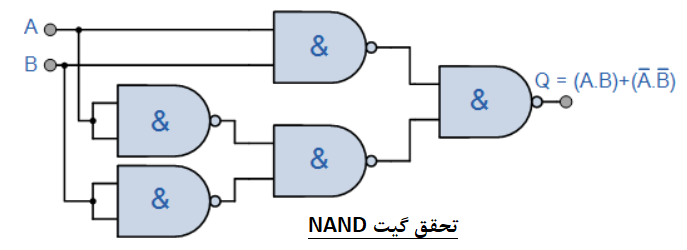
یکی از معایب اصلی، پیاده‌سازی تابع XNOR در بالا، این است؛ که شامل سه ‌نوع مختلف از گیت‌های منطقی، AND، NOT و درنهایت OR در طراحی پایه‌ی خود می‌شود. یک راه آسان‌تر برای ایجاد تابع Ex-NOR، از یک نوع گیت تنها، استفاده از گیت‌های NAND است؛ که در زیر نشان داده شده‌است.

تحقق گیت XNOR با استفاده از گیت‌های NAND

گیت‌های XNOR عمدتا در مدارهای الکترونیکی، که عملیات حسابی و چک‌کردن داده را انجام می‌دهند؛ مانند جمع‌کننده‌ها، تفریق‌گرها و چک‌کننده‌های برابری و… استفاده می‌شوند. از آنجایی‌که، تابع Ex-NOR، زمانی‌که دو خروجی برابر باشند؛ خروجی را در سطح منطقی “1” را ارائه می‌دهد؛ می‌تواند برای مقایسه‌ی دو رقم یا اعداد باینری استفاده شود؛ از این رو گیت‌های XNOR در مدارهای مقایسه‌کننده‌ی دیجیتال، استفاده می‌شوند.

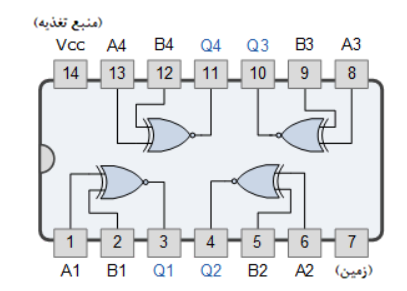
آیسی گیت منطقی دیجیتال Exclusive-NOR که معمولا دردسترس است؛ شامل:

TTL- گیت منطقی XNOR

CMOS- گیت منطقی XNOR

گیت XNOR دو ورودی چهارتایی 74266

در مقاله بعدی در مورد گیت‌های منطقی دیجیتال، بافر سه‌حالته که بافر غیر وارونگر نیز نامیده می‌شود؛ را در هردو مدار منطقی TTL و CMOS ، به‌همراه تعریف جبر بولی و جدول درستی آن، بررسی خواهیم‌کرد.