با دسته بندی اعداد باینری در گروه ها و مجموعههای چهارگانه (چهار بیتی) در صورتی که هر رقم بتواند ۱۶ وضعیت مختلف را تجربه کند، مفهوم اعداد هگزادسیمال پدید می آید.
یکی از اصلیترین ضعفها و معایب اعداد باینری در تبدیل اعداد دسیمال به اعداد باینری، طولانی بودن بیش از حد رشتههای باینری معادل اعداد دسیمال بزرگ است.
در سیستمهای دیجیتالی مانند رایانهها، استفاده از اعداد باینری ۸، ۱۶ و ۳۲ رقمی بسیار رایج است. این در حالی است که، خواندن و نوشتن تعداد زیادی عدد باینری ۱۶ یا ۳۲ بیتی، بدون ایجاد خطا و اشتباه بسیار دشوار خواهد بود.
دسته بندی اعداد باینری در گروهها و یا مجموعههای چهار بیتی، یکی از روشهای رایج به منظور رفع این مشکل است. این گروههای چهار بیتی از نوعی سیستم شماره گذاری، که معمولا در سیستمهای دیجیتال با نام اعداد هگزادسیمال شناخته میشوند، پیروی میکنند.
سیستم شماره گذاری هگزادسیمال و یا هگز (Hex)، یک دستگاه اعداد بر مبنای 16 (Base of 16) است. از جمله ویژگیهای این سیستم، استفاده از فرمت کاملا فشرده است. این ویژگی سبب میشود، که این سیستم شماره گذاری، گزینه بسیار مناسبی به منظور نمایش رشتههای باینری طولانی محسوب شود، از طرفی درک آن در مقایسه با رشتههای باینری طولانی متشکل از 0 و 1 بسیار آسانتر خواهد بود.
سیستم شماره گذاری هگزادسیمال بر مبنای ۱۶ تعریف میشود، به عبارت دیگر برای نمایش اعداد در این سیستم، هر رقم میتواند ۱۶ وضعیت مختلف حاصل ترکیبی از اعداد (۰ تا ۱۵) را اختیار کند.
اعداد دسیمال ۱۵ ، ۱۴ ، ۱۳ ، ۱۲ ، ۱۱ ، ۱۰ دارای دو رقم هستند. زمانیکه این اعداد بر مبنای ۱۶ نوشته میشوند، برای مثال در اعداد ۱۰ و ۱۱ تشخیص باینری و یا دسیمال بودن اعداد مشکل خواهد بود.
برای مثال زمانیکه عدد 10 بر مبنای 16 (سیستم هگزادسیمال) نوشته شود، تشخیص اینکه این عدد نماینده عدد 2 (1+0) در سیستم شماره گذاری باینری و یا نماینده عدد 10 در سیستم دسیمال است، ممکن نخواهد بود. به منظور حل این مشکل، اعداد هگزادسیمال با مقادیر 15 ، 14 ، 13 ، 12 ، 11 ، 10 به ترتیب با حروف بزرگ A ، B ، C ، D ، F جایگزین خواهند شد.
بنابراین در سیستم شماره گذاری هگزادسیمال، از ارقام 0 تا 9 و حروف بزرگ A تا F به منظور نمایش معادل اعداد باینری و دسیمال استفاده میشود. در این سیستم نیز مانند سیستم اعداد دسیمال و باینری، اولین رقم از سمت راست دارای کمترین ارزش خواهد بود.
همانطور که در ابتدا اشاره شد، خواندن رشتههای بسیار طولانی باینری دشوار است، از این رو با تقسیم و دسته بندی کردن این اعداد به گروههای کوچکتر با اندازه و ارقام مساوی، درک آنها راحتتر خواهد شد. برای مثال خواندن و نوشتن گروه ارقام ۱۱۱۱۲ ۱۱۰۰ ۰۱۰۱ ۱۱۰۱ به مراتب سادهتر از عدد ۱۱۰۱۰۱۰۱۱۱۰۰۱۱۱۱۲ است.
در استفاده روزانه از سیستم شماره گذاری دسیمال (اعشاری)، به منظور درک سادهتر اعداد چند میلیونی و میلیاردی، ارقام از سمت راست به مجموعههای سه رقمی گروه بندی میشوند. مشابه با این روش برای ساده سازی رشته عددهای دیجیتالی نیز استفاده میشود.
سیستم شماره گذاری هگزادسیمال نسبت به سیستمهای شماره گذاری دسیمال و باینری پیچیدگی بیشتری دارند. این اعداد عمدتا در کامپیوترها و جهت آدرس دهی مکانهای حافظه استفاده می٬شوند. با تقسیم یک عدد باینری به گروهها چهار بیتی، هر گروه یا مجموعه ۴ رقمی میتواند، دارای مقادیری بین ۰۰۰۰ باینری (صفر) تا ۱۱۱۱ باینری (۱۵) را اختیار کنند، به بیان دیگر در مجموع ۱۶ وضعیت مختلف از ترکیب ارقام ۰ تا ۱۵ وجود خواهد داشت.
با توجه به آموزشهای بخش تبدیل اعداد باینری به اعداد دسیمال، هر گروه 4 بیتی یک نیبل (nibble) نامیده میشود. از طرفی تولید هر عدد هگزادسیمال، به حداقل 4 بیت نیازمند است، بنابراین هر عدد هگزادسیمال میتواند به عنوان یک نیبل و یا نصف یک بایت (half-a-byte) درنظر گرفته شود. واضح است که جهت تولید یک بایت به دو رقم هگزادسیمال از 00 تا FF نیاز است.
در سیستم شماره گذاری دسیمال عدد ۱۶ معادل توان چهارم ۲ یا (۲۴) است، بنابراین ارتباط مستقیمی بین دو عدد 2 و 16 وجود دارد. در نتیجه یک رقم هگزادسیمال ارزشی معادل 4 رقم باینری خواهد داشت. در فرمول کلی نمایش سیستمهای شماره گذاری، مقدار q مربوط به دستگاه اعداد هگزادسیمال 16 است.
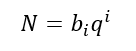
با توجه به این رابطه، میتوان چهار رقم در یک عدد باینری را معادل با یک رقم هگزادسیمال در نظر گرفت. این امر تبدیل اعداد باینری به اعداد هگزادسیمال و بالعکس را بسیار ساده خواهد کرد، همچنین نمایش اعداد باینری بزرگ با تعداد ارقام بسیار کمتر به صورت هگزادسیمال را ممکن خواهد کرد.
رابطه ی بین اعداد دسیمال، باینری و هگزادسیمال در جدول زیر معرفی شده است. اعداد 0 تا 9 به صورت مشترک در هر دو دستگاه اعداد دسیمال و هگزادسیمال استفاده میشوند، این در حالی است که اعداد دسیمال 10 تا 15 معادل حروف بزرگ A تا F در دستگاه اعداد هگزادسیمال خواهد بود.
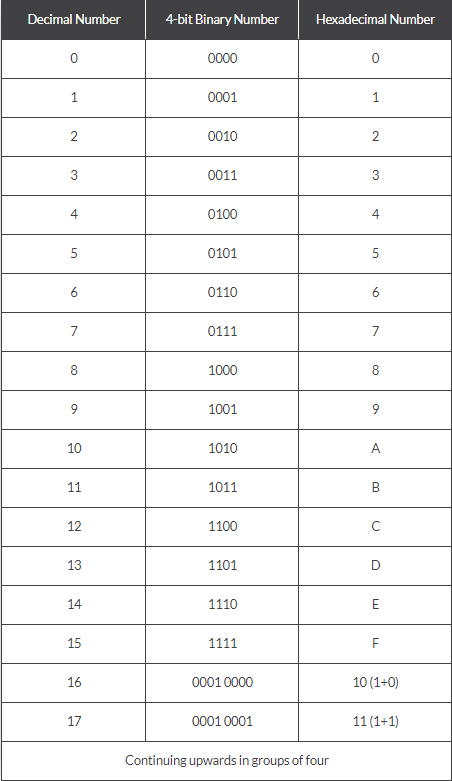
با استفاده از جدول بالا، عدد باینری ۱۱۱۱۲ 1100 0101 1101 میتواند به صورت یک عدد هگزادسیمال D5CF معرفی شود که خواندن و درک آن به مراتب ساده تر از یک رشته طولانی متشکل از ارقام 0 و 1 است.
بنابراین با استفاده از اعداد هگزادسیمال، اعداد دیجیتال را میتوان با استفاده از ارقام کمتر و همچنین احتمال بروز خطا کمتر بازنویسی کرد. به صورت مشابه تبدیل اعداد هگزادسیمال به اعداد باینری نیز امکان پذیر خواهد بود.
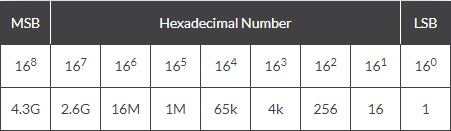
یکی از ویژگیهای اصلی سیستم شماره گذاری هگزادسیمال وجود 16 رقم شمارش مجزا و متفاوت از 0 تا F است که در آن وزن هر رقم 16 برابر رقم قبلی خواهد بود. اولین رقم از سمت راست دارای کمترین ارزش (LSB) است. به منظور متمایز کردن اعداد هگزادسیمال از اعداد دسیمال از پیشوند # (Hash) و یا $ (Dollar singn) قبل از اعداد هگزادسیمال استفاده خواهد شد. برای مثال D5CF# و یا D5CF$، همچنین میتوان از زیر نویس 16 برای شناسایی اعداد هگزادسیمال استفاده کرد. برای مثال D5CF۱۶ .
شمارش با استفاده از اعداد هگزادسیمال (Counting using Hexadecimal Numbers)
تاکنون، نحوه تبدیل چهار رقم باینری به یک عدد دسیمال معرفی شده است. در ادامه تبدیل اعداد باینری دارای ارقام بیشتر از 4 به اعداد هگزادسیمال بررسی خواهد شد. شمارش اعداد هگزادسیمال پس از حرف F به صورت زیر خواهد بود:
![]()
واضح است که اعداد 20 یا 10 به اعداد دسیمال اشاره ندارند و در واقع آنها نماینده 2+0 و 1+0 در دستگاه اعداد هگزادسیمال هستند. یک مجموعه دو عددی هگزادسیمال، میتواند تا عدد FF معادل عدد دسیمال 255 را تولید کند. به همین ترتیب، مجموعه سه عددی هگزادسیمال، میتواند تا عدد 100۱۶، (۲۵۶۱۰) معادل عدد دسیمال FFF۱۶، (۴۰۹۵۱۰) و مجموعه چهار رقمی هگزادسیمال FFF۱۶ معادل عدد دسیمال ۶۵۵۳۵ را تولید کند.
نمایش یک عدد هگزادسیمال (Representation of a Hexadecimal Number)
در صورتی که تعداد بیتهای عدد باینری مضاربی صحیحی از عدد 4 باشند (4,8,12,16)، تبدیل اعداد باینری و دسیمال به اعداد هگزادسیمال بسیار ساده خواهد بود. اما در صورتی که تعداد بیتهای عدد باینری مضرب صحیحی از چهار نباشند، با افزودن تعداد مناسبی صفر در سمت چپ پر ارزشترین بیت (MSB)، تعداد بیتهای عدد باینری به میزان مورد نظر افزایش خواهد یافت.
برای مثال تعداد ارقام عدد باینری ۱۱۰۰۱۰۱۱۰۱۱۰۰۱۲ برابر 14 است. تعداد ارقام این عدد جهت نمایش در قالب سه رقم هگزادسیمال زیاد و همچنین برای تعریف در قالب چهار رقم هگزادسیمال بسیار کوچک است. با اضافه کردن دو صفر در سمت چپ پر ارزشترین رقم عدد باینری (MSB)، تعداد ارقام عدد به 16 که مضرب صحیحی از عدد 4 است افزایش مییابد. افزودن صفر پس از رقم MSB تغییری در مقدار عدد باینری ایجاد نخواهد کرد. بنابراین معادل هگزادسیمال عدد باینری 11001011011001۲ برابر با ۰۰۱۱۰۰۱۰۱۱۰۱۱۰۰۱۲ و به صورت 32D9۱۶ است.
افزودن صفر های اضافی به یک عدد باینری (Adding of Additional 0’s to a Binary Number)

سیستم شماره گذاری هگزادسیمال بر مبنای ۱۶ است، بنابراین تعداد ارقام مورد استفاده جهت نمایش یک عدد معمولا کمتر از معادل عدد در سیستم شماره گذاری باینری یا دسیمال خواهد بود. از طرفی تبدیل اعداد هگزادسیمال به باینری و بالعکس بسیار ساده است.
مثال شماره ۱
معادل هگزادسیمال عدد باینری ۱۰۱۰۲ ۱۱۱۰ به صورت زیر محاسبه میشود.
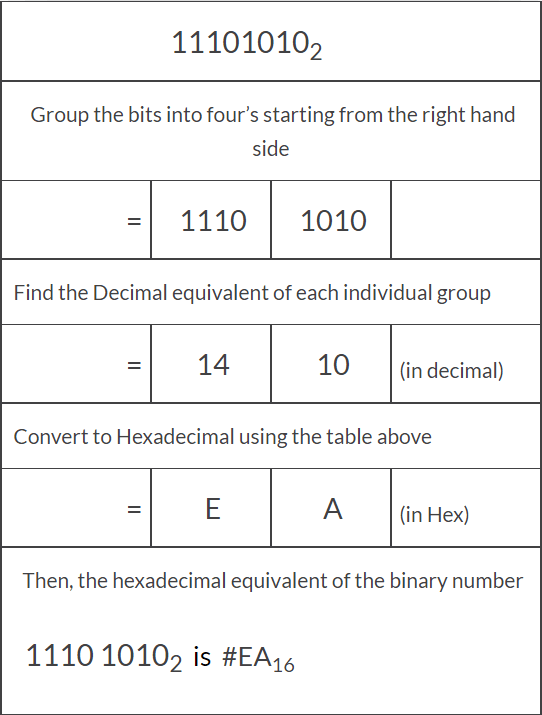
بنابراین معادل هگزادسیمال عدد باینری ۱۰۱۰۲ 1110 برابر با EA۱۶ خواهد بود.
مثال شماره ۲
معادل باینری و دسیمال عدد هگزادسیمال 3FA7۱۶ # به صورت زیر محاسبه میشود.
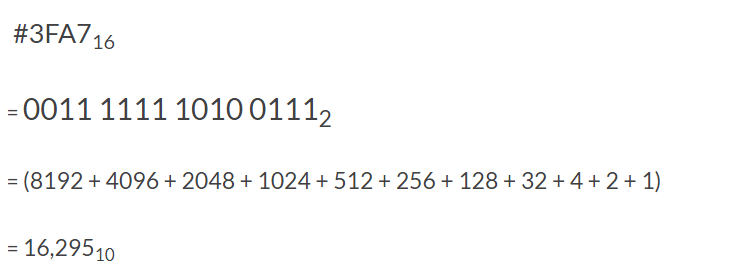
خلاصه
در سیستمهای دیجیتالی و کامپیوترها با استفاده از سیستم شماره گذاری هگزادسیمال یا هگز، جهت درک راحتتر و جلوگیری از بروز خطا، رشتههای طولانی اعداد باینری را به مجموعههای چهار رقمی تبدیل میکنند. واژه هگزادسیمال در لاتین به معنای شانزده است که علت نامگذاری این سیستم شماره گذاری، استفاده از 16 رقم مختلف 0 تا 9 و A تا F برای معرفی اعداد است.
جهت تبدیل یک عدد باینری به معادل عدد هگزادسیمال، ابتدا ارقام عدد باینری در مجموعههای چهار بیتی گروه بندی خواهند شد. این مجموعههای باینری میتوانند هر مقدار از (۰۰۰۰۲) ۰۱۰ تا ۱۵۱۰ (۱۱۱۱۲) را اختیار کنند که معادل عدد هگزادسیمال 0 تا F خواهد بود.


دیدگاه خود را بنویسید