امپدانس که بر حسب اهم اندازه‌گیری میشود؛ در واقع همان مقاومت موثر در برابر جریان جاری در یک مدار AC است که از مقاومت و راکتانس (reactance) تشکیل شده است.
درمقاله‌های قبلی، مشاهده کردیم؛ که در یک مدار AC حاوی شکل موج سینوسی، از فازورهای ولتاژ و جریان، به همراه اعداد مختلط، می‌توان برای نشان دادن یک کمیت مختلط استفاده کرد.همچنین دیدیم، که شکل موج‌های سینوسی و توابعی را که قبل از این، برای تبدیل در حوزه زمان ترسیم شده بودند؛ می‌توان به حوزه‌ی فضایی یا فازور تبدیل کرد؛ تا نمودارهای فازوری، برای یافتن رابطه‌ی ولتاژ-جریان فازور ساخته شوند.
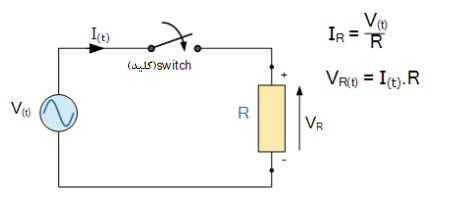
هر عنصر اساسی ایده‌آل مدار؛ مانند مقاومت را، می‌توان از نظر ولتاژ و جریان، به صورت ریاضیاتی توصیف کرد. در آموزش مرتبط با مقاومت‌ها دیدیم؛ که ولتاژ روی یک مقاومت اهمی خالص، به طور خطی، متناسب با جریان عبوری از آن می‌باشد؛ که توسط قانون اهم تعریف شده است. مدار زیر را در نظر بگیرید.
مقاومت AC با منبع سینوسی
1. مقاومت AC با منبع سینوسی
زمانی‌که، یک کلید بسته میشود؛ یک ولتاژ AC (V ) به مقاومت ( R) اعمال می‌گردد؛ این ولتاژ، سبب جاری شدن جریان می‌گردد، که در نتیجه، با بالا و پایین رفتن سینوسی ولتاژ، جریان نیز افت و خیز می‌یابد. به دلیل اینکه، بار خود یک مقاومت است؛ جریان و ولتاژ هر دو با یک‌دیگر به مقدار حداکثر یا پیک خود رسیده و سپس هم‌زمان، تا صفر افت می‌کنند. این بدین معناست که بالا و پایین رفتن هردو، هم‌زمان بوده و بنابراین “هم فاز” می‌باشند.
درنتیجه، جریان الکتریکی که از طریق یک مقاومت AC جریان می‌یابد؛ در زمان به صورت سینوسی تغییر می‌کند و با عبارت روبرو نشان داده میشود: I(t) = Im x sin(ωt + θ), در این عبارت ، Im حداکثر دامنه جریان است و زاویه فاز می‌باشد. علاوه بر این، همچنین می‌توان گفت، که برای هر جریان معین ( I) جاری در مقاومت، مقدار حداکثر یا پیک ولتاژ که از ترمینال‌های R می‌گذرد، با قانون اهم به صورت زیر ارائه می‌گردد:
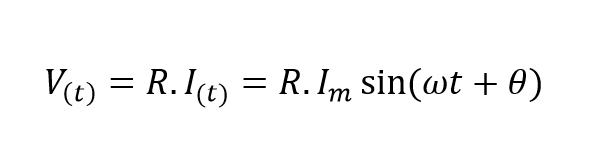
همچنین برای مقدار لحظه‌ای جریان خواهیم داشت:
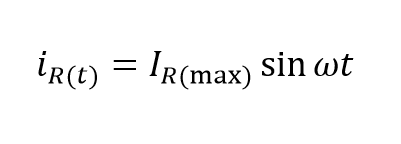
بنابراین، برای یک مدار مقاومتی خالص، جریان متناوب عبوری از مقاومت، متناسب با ولتاژ اعمال شده و مطابق با همان الگوی سینوسی تغییر می‌کند. به دلیل مشترک بودن فرکانس منبع تغذیه، برای ولتاژ و جریان، فازور های آن‌ها نیز مشترک بوده که منجر میشود؛ جریان با ولتاژ “هم‌فاز” باشد. ( θ = ۰ ).
به عبارت دیگر، در هنگام استفاده از مقاومت AC، بین جریان و ولتاژ، اختلاف فازی وجود ندارد و هر زمان که ولتاژ، به حداکثر، حداقل و صفر خود برسد، هم‌زمان با آن، جریان نیز به حداکثر، حداقل و صفر خود می‌رسد. همانطور که در زیر نشان داده شده‌است.
شکل موج سینوسی برای مقاومت AC
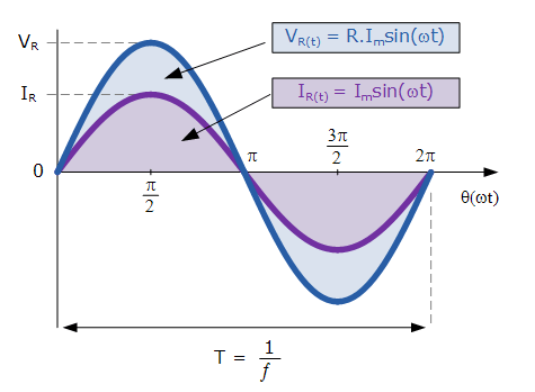2. شکل موج سینوسی مقاومت در مدار AC
این اثر هم فاز بودن را، می‌توان با یک نمودار فازوری نشان داد. در حوزه‌ی مختلط، مقاومت یک عدد حقیقی است؛ به این معنا که دارای هیچ مولفه ” j” یا مولفه‌ی موهومی نیست. بنابراین، چون ولتاژ و جریان با هم، هم‌فاز می‌باشند؛ هیچ اختلاف فازی، میان این دو وجود نخواهد داشت ( θ = ۰ ). در نتیجه، بردارهای هر کمیت، به صورت سوار شده بر یک‌دیگر، در راستای یک محور مرجع رسم می‌شوند. این تبدیل از حوزه زمان-سینوسی به حوزه فازور در زیر نمایش داده شده است.
نمودار فازوری برای مقاومت AC
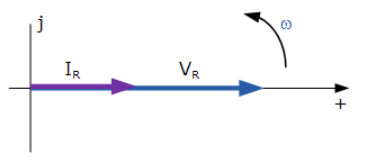3. نمودار فازوری برای مقاومت AC
یک فازور، مقادیر RMS کمیت‌های ولتاژ و جریان را، برخلاف بردار، که نشان‌دهنده‌ی مقادیر پیک یا حداکثر است، نشان میدهد. با تقسیم مقدار پیک در حوزه‌ی زمان بر ۲√ رابطه‌ی فازور ولتاژ-جریان به صورت زیر به دست می‌آید:
رابطه RMS
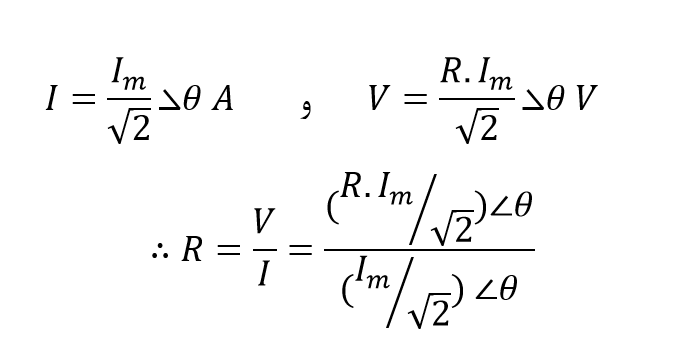
رابطه فازور
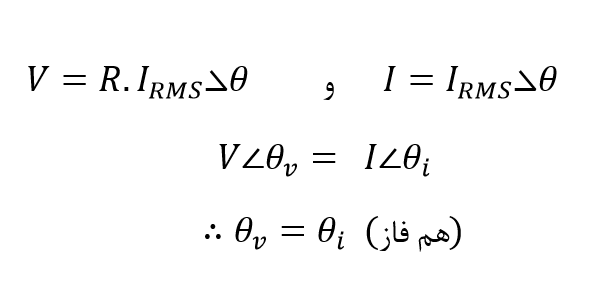
این نشان میدهد که یک مقاومت خالص درون مدار AC ، رابطه‌ی میان فازورهای ولتاژ و جریان را، دقیقا به همان روشی ایجاد می‌کند که همان مقاومت‌ها، رابطه ولتاژ و جریان را در مدار DC ایجاد می‌کنند.
درهرحال، در یک مدار DC، این رابطه مقاومت خوانده میشود که توسط قانون اهم بیان میشود؛ در حالی‌که، در یک مدار سینوسی AC، رابطه‌ی ولتاژ-جریان، امپدانس خوانده میشود. به عبارت دیگر، مقاومت الکتریکی در مدار AC، “امپدانس” خوانده میشود.
در هر دو مورد، این رابطه‌ی ولتاژ-جریان ( V-I) همیشه در یک مقاومت خالص، خطی است. در مدارهای AC، زمانی که از عبارت امپدانس استفاده میشود؛ به معنای مقاومت آن مدار است که با نماد Z نشان داده میشود. از این رو به درستی می‌توانیم برای مقاومت بیان کنیم که : مقاومت DC= مقاومت AC یا R=Z.
بردار امپدانس با حرف Z برای مقدار مقاومت AC برحسب اهم ( Ω ) نمایش داده میشود که همانند DC آن است. در نتیجه می‌توان امپدانس (یا مقاومت AC) را چنین تعریف کرد:
امپدانس AC
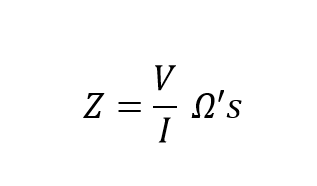
امپدانس، را با یک عدد مختلط نیز می‌توان نشان داد؛ زیرا این امر به فرکانس مدار، بستگی دارد (ω در زمانی که اجزای واکنشی در مدار وجود داشته باشند). اما در یک مدار مقاومتی خالص، مقدار این اجزای واکنشی همیشه برابر با صفر خواهد بود و بیان کلی برای امپدانس در یک مدار کاملا مقاومتی، که با یک عدد مختلط بیان می‌گردد خواهد بود:
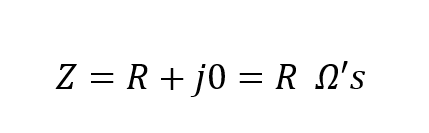
از آنجایی که، زاویه فاز، بین ولتاژ و جریان در یک مدار AC کاملا مقاومتی، برابر با صفر است؛ ضریب توان نیز باید صفر باشد و به صورت روبرو بیان شود: cos 0o = ۱.۰ سپس توان لحظه‌ای مصرفی در مقاومت خواهد بود:
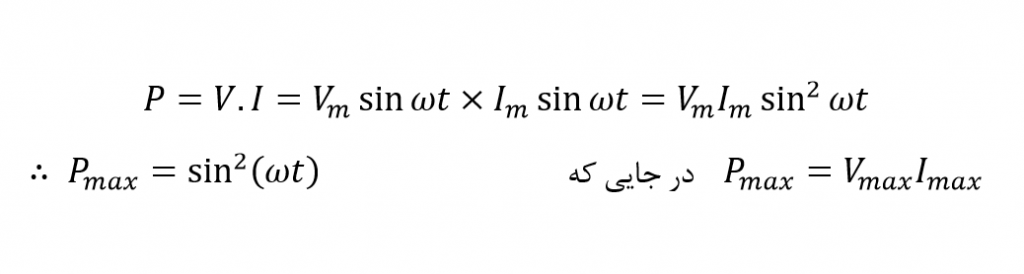
چون توان متوسط، در مدار مقاومتی یا واکنشی به زاویه‌ی فاز بستگی دارد و در یک مدار کاملا مقاومتی θ = ۰ است؛ ضریب توان برابر با ۱ می‌باشد. بنابراین می‌توان، با استفاده از قانون اهم، توان متوسط مصرفی در یک مقاومت AC را به صورت زیر تعریف کرد:
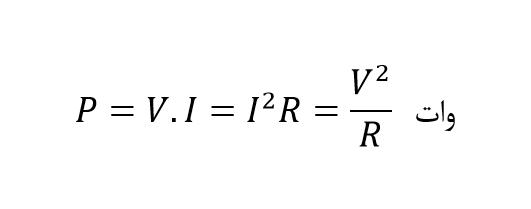
که در واقع، همان معادلات قانون اهم می‌باشد که در مدارهای DC برقرار است. درنتیجه، توان موثر مصرفی در یک مقاومت AC برابر با توان مصرفی توسط همان مقاومت در مدار DC است.
بسیاری از مدارهای AC مانند عناصر گرمایشی و لامپ‌ها، تنها از یک مقاومت اهمی خالص تشکیل شده‌اند و مقادیر ناچیز القایی یا خازنی حاوی امپدانس دارند.
در چنین مدارهایی، ما می‌توانیم از قانون اهم یا قانون کیرشهف و همچنین قوانین ساده مدار، برای محاسبه و یافتن ولتاژ، جریان، امپدانس و توان، مانند تجزیه و تحلیل DC استفاده کنیم و هنگام کار با چنین قوانینی معمولا استفاده از مقادیر RMS معمول‌تر است.
مثال شماره 1 - مقاومت AC
یک عنصر گرمایشی الکتریکی که دارای مقاومت AC شصت اهم است به یک منبع تغذیه تک فاز ۲۴۰ ولت متصل است. جریان دریافتی از منبع و توان مصرف شده توسط عنصر گرمایشی را محاسبه کنید. همچنین نمودار فازوری مربوطه را که رابطه فاز بین جریان و ولتاژ را نشان میدهد، ترسیم کنید.
جریان منبع:
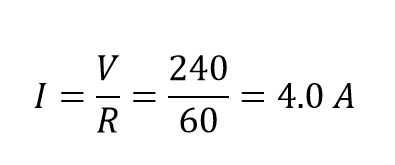
توان فعال مصرفی توسط مقاومت AC به صورت زیر محاسبه میشود:
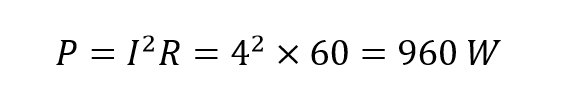
از آنجایی که هیچ اختلاف فازی بین اجزای مقاومتی وجود ندارد ( θ = ۰ ) نمودار فازوری مربوطه به صورت زیر ارائه میشود:
۴. نمودار فازوری برای حالت ( θ = ۰ )
مثال شماره 2 - مقاومت AC
منبع تغذیه‌ی ولتاژ سینوسی به صورت روبرو تعریف میشود: که به مقاومت خالص ۵۰ اهم متصل است. امپدانس آن و مقدار پیک جریان عبوری از مدار را تعیین کنید. نمودار فازور مربوطه را نیز رسم کنید.
ولتاژ سینوسی دو سر مقاومت، همان است که در یک مدار کاملا مقاومتی خواهد بود. با تبدیل این ولتاژ از حوزه زمان به حوزه فازور خواهیم داشت:
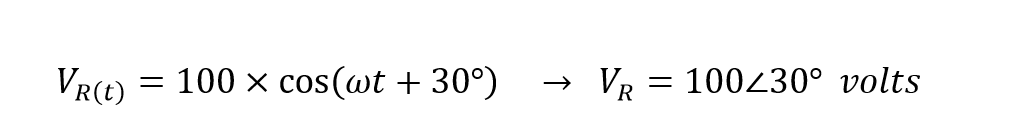
استفاده از قانون اهم به ما میدهد:
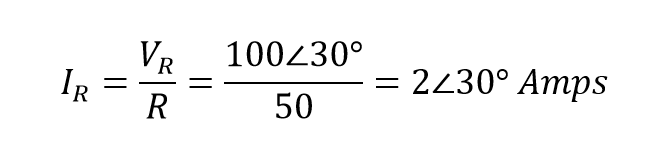
نمودار فازوری مربوطه به صورت زیر خواهد بود:
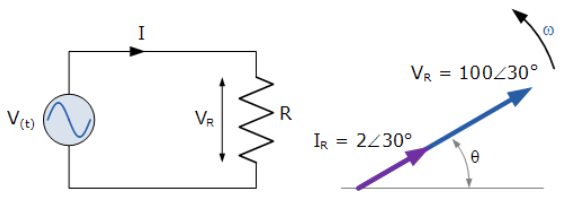۵. نمودار فازوری مثال ۲
خلاصه امپدانس
در یک مقاومت AC خالص اهمی، جریان و ولتاژ هردو، “هم‌فاز” می‌باشند؛ زیرا هیچ اختلاف فازی میان آن‌ها وجود ندارد. جریان عبوری از مقاومت، مستقیما متناسب با ولتاژ دو سر آن است و این رابطه‌ی خطی در مدار AC، امپدانس نامیده میشود.
امپدانس، که با حرف انگلیسی Z نمایش داده میشود؛ در یک مقاومت اهمی خالص، یک عدد مختلط است؛ که فقط از یک بخش حقیقی تشکیل میشود؛ که مقدار حقیقی مقاومت AC (R ) بوده و دارای یک بخش موهومی صفر(j0) است. به همین دلیل، قانون اهم را می‌توان در مدارهای حاوی مقاومت AC، برای محاسبه‌ی ولتاژها و جریان‌ها استفاده کرد.
در مقاله بعدی، در مورد اندوکتانس AC، به رابطه‌ی ولتاژ-جریان یک سلف، زمانی‌که یک شکل‌موج سینوسی حالت مانا به آن اعمال میشود؛ به همراه نمایش نمودار فازوری آن برای اندوکتانس خالص و ناخالص، خواهیم پرداخت.
دیدگاه خود را بنویسید