راکتانس سلفی

راکتانس سلفی یک سیم‌پیچ به فرکانس ولتاژ اعمال شده بستگی دارد زیرا راکتانس مستقیما با فرکانس متناسب است. تاکنون به رفتار سلف‌های متصل به منابع DC نگاه کرده‌ایم و امیدواریم تاکنون متوجه شده باشید که وقتی یک ولتاژ DC بر یک سلف اعمال می‌شود، رشد جریان از طریق آن فوری نیست، بلکه توسط اندوکتانس خودالقاشده یا مقدار نیروی محرکه مخالف تعیین می‌شود. همچنین دیدیم که جریان سلف‌ها تا زمانی که پس از پنج ثابت زمانی به حداکثر حالت پایدار خود برسد، به افزایش خود ادامه می‌دهد. حداکثر جریان عبوری از یک سیم‌پیچ فقط توسط قسمت مقاومتی سیم‌پیچ بر حسب اهم محدود می‌شود و همانطور که از قانون اهم می‌دانیم، این با نسبت ولتاژ به جریان V/R تعیین می‌شود.

هنگامی که یک ولتاژ متناوب یا AC بر یک سلف اعمال می‌شود، عبور جریان از آن رفتار بسیار متفاوتی نسبت به حالتی که ولتاژ DC اعمال شده باشد، خواهد داشت. اثر منبع سینوسی باعث ایجاد اختلاف فاز بین شکل موج ولتاژ و جریان می‌شود. اکنون در یک مدار AC، مخالفت با جریان از طریق سیم‌پیچ‌ها نه تنها به اندوکتانس سیم‌پیچ، بلکه به فرکانس شکل موج AC نیز بستگی دارد. مخالفت با جریان عبوری از سیم‌پیچ در مدار AC توسط مقاومت AC که بیشتر به عنوان امپدانس (Z) معروف است، تعیین می‌شود.

اما مقاومت همیشه با مدارهای DC مرتبط است، بنابراین برای تشخیص مقاومت DC از مقاومت AC معمولا از اصطلاح راکتانس استفاده می‌شود. درست مانند مقاومت، مقدار راکتانس نیز با اهم اندازه‌گیری می‌شود، اما نماد X به آن داده می‌شود تا آن را از یک مقدار کاملا مقاومتی متمایز کند. از آنجایی که جزء مورد علاقه ما یک سلف است، راکتانس یک سلف را «راکتانس سلفی» می‌نامند. به عبارت دیگر، مقاومت الکتریکی سلف در هنگام استفاده در مدار AC را راکتانس سلفی می‌نامند. راکتانس سلفی که نماد XL به آن داده می‌شود، خاصیتی در مدار AC است که با تغییر جریان مخالف است. در مقالات خازن‌ها در مدارهای متناوب دیدیم که در یک مدار کاملا خازنی، جریان IC 90 درجه از ولتاژ «جلو» می‌افتد. در یک مدار AC فقط سلفی دقیقا برعکس است، جریان IL از ولتاژ اعمال شده ۹۰ درجه (یا  رادیان) «عقب» می‌افتد.

مدار سلفی AC

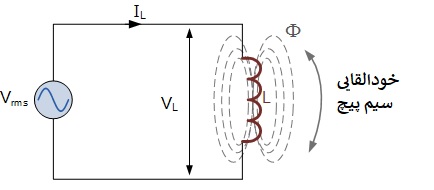1) مدار سلفی AC

در مدار کاملا سلفی بالا، سلف مستقیما به ولتاژ تغذیه AC وصل می‌شود. با افزایش و کاهش ولتاژ تغذیه با فرکانس، نیروی محرکه مخالف خودالقاشده نیز با توجه به این تغییر در سیم‌پیچ افزایش و کاهش می‌یابد. می‌دانیم که این نیروی محرکه خودالقایی مستقیما با نرخ تغییر جریان از طریق سیم‌پیچ متناسب است و زمانی که ولتاژ تغذیه از نیم‌سیکل مثبت به نیم‌سیکل منفی یا بالعکس در نقاط صفر درجه و ۱۸۰ درجه در امتداد موج سینوسی عبور می‌کند، به بیشترین مقدار خود می‌رسد. در نتیجه، حداقل نرخ تغییر ولتاژ زمانی اتفاق می‌افتد که موج سینوسی AC در حداکثر یا حداقل سطح ولتاژ پیک خود باشد. در این موقعیت‌ها در سیکل، حداکثر یا حداقل جریان از مدار سلف عبور می‌کند و این در زیر نشان داده شده است.

دیاگرام فازی سلف AC

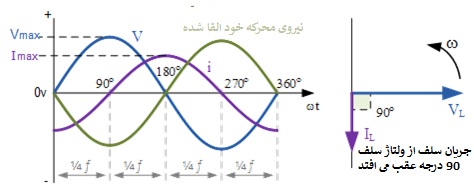2) دیاگرام فازی سلف AC

این شکل موج‌های ولتاژ و جریان نشان می‌دهد که برای یک مدار سلفی صرف، جریان ۹۰ درجه از ولتاژ عقب می‌افتد. به همین ترتیب، می‌توان گفت که ولتاژ ۹۰ درجه از جریان جلو می‌افتد. در هر صورت، عبارت کلی این است که همانطور که در نمودار برداری نشان داده شده است، جریان تاخیر دارد. در اینجا بردار جریان و بردار ولتاژ با اختلاف ۹۰ درجه نشان داده شده‌اند. جریان از ولتاژ عقب می‌افتد. همچنین می‌توانیم این عبارت را به صورت VL = ۰o و IL = -۹۰o با توجه به ولتاژ VL بنویسیم. اگر شکل موج ولتاژ به عنوان موج سینوسی طبقه‌بندی شود، جریان،  IL را می‌توان به عنوان کسینوس منفی طبقه‌بندی کرد و می‌توانیم مقدار جریان را در هر نقطه از زمان به صورت زیر تعریف کنیم:

که در فرمول بالا ω واحد رادیان بر ثانیه و t واحد ثانیه دارند.

از آنجایی که جریان همیشه در یک مدار صرف سلفی 90 درجه از ولتاژ عقب می‌افتد، می‌توانیم فاز جریان را با دانستن فاز ولتاژ یا بالعکس پیدا کنیم. بنابراین اگر مقدار VL را بدانیم،  IL باید 90 درجه عقب بیفتد. به همین ترتیب، اگر مقدار IL را بدانیم، بنابراین VL باید 90 درجه پیشروی کند. پس این نسبت ولتاژ به جریان در یک مدار سلفی معادله ای را ایجاد می‌کند که راکتانس سلفی XL سیم‌پیچ را تعریف می‌کند.

راکتانس سلفی

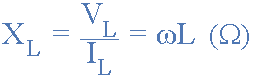
می‌توانیم معادله بالا را برای راکتانس سلفی به شکلی آشناتر بازنویسی کنیم که از فرکانس معمولی منبع تغذیه به جای فرکانس زاویه‌ای ω بر حسب رادیان استفاده می‌کند و به صورت زیر داده می‌شود:

که f فرکانس و L مقدار اندوکتانس سلف و 2πƒ = ω است.

از معادله بالا برای راکتانس سلفی می‌توان دریافت که اگر یکی از مقادیر فرکانس یا اندوکتانس افزایش یابد، مقدار کلی راکتانس القایی نیز افزایش می‌یابد. همانطور که فرکانس به بی‌نهایت نزدیک می‌شود، راکتانس سلف نیز تا بی‌نهایت افزایش می‌یابد که مانند یک مدار باز عمل می‌کند. با این حال، با نزدیک شدن فرکانس به صفر یا DC، راکتانس سلف به صفر کاهش می‌یابد و مانند یک اتصال کوتاه عمل می‌کند. این بدان معنی است که راکتانس سلفی «متناسب» با فرکانس است. به عبارت دیگر، راکتانس سلفی با فرکانس افزایش می‌یابد که در نتیجه XL در فرکانس‌های پایین کوچک و در فرکانس‌های بالا زیاد است و این در نمودار زیر نشان داده شده است:

نمودار راکتانس سلفی در برابر تغییر فرکانس

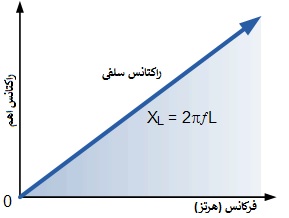3) نمودار راکتانس سلفی در برابر تغییر فرکانس

شیب نشان می‌دهد که «راکتانس سلفی» یک سلف با افزایش فرکانس منبع تغذیه در سراسر آن افزایش می‌یابد. بنابراین راکتانس سلفی با فرکانس داده شده متناسب است (XL α ƒ) پس می‌توانیم ببینیم که در فرکانس DC، یک سلف راکتانس صفر (اتصال کوتاه) دارد و در فرکانس‌های بالا راکتانس بی‌نهایت (اتصال باز) دارد.

مثال 1) راکتانس سلفی
یک سیم‌پیچ با اندوکتانس ۱۵۰ میلی‌هانری و مقاومت صفر به یک منبع تغذیه ۱۰۰ ولت ۵۰ هرتزی متصل شده است. راکتانس سلفی  و مقدار جریان عبوری از آن را بیابید.

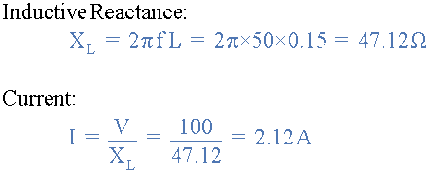
اتصال منبع تغذیه AC از طریق مدار سری LR

تا اینجا ما یک سیم‌پیچ کاملا سلفی را در نظر گرفتیم، اما غیرممکن است که یک اندوکتانس خالص داشته باشیم زیرا همه سیم‌پیچ‌ها، رله‌ها یا سلونویید‌ها مقدار مشخصی از مقاومت را دارند و مهم نیست که چقدر با دورهای سیم‌پیچ مورد استفاده مرتبط باشد. پس می‌توانیم سیم‌پیچ ساده خود را به عنوان یک مقاومت سری با یک اندوکتانس در نظر بگیریم.

در مدار AC که دارای هر دو اندوکتانس L و مقاومت R است، ولتاژ V، مجموع فاز دو ولتاژ VR و VL خواهد بود. این بدان معناست که جریانی که از سیم‌پیچ می‌گذرد، همچنان از ولتاژ عقب می‌ماند، اما بسته به مقادیر VR و VL، مقدار کمتر از ۹۰ درجه خواهد داشت. زاویه فاز جدید بین ولتاژ و جریان به عنوان زاویه فاز مدار شناخته می‌شود و نماد یونانی فی Φ داده می‌شود. برای اینکه بتوان یک نمودار برداری از رابطه بین ولتاژ و جریان تولید کرد، باید یک مرجع یا جزء مشترک پیدا کرد. در یک مدار R-L متصل سری، جریان مشترک است زیرا جریان یکسانی از هر جز عبور می‌کند. بردار این کمیت مرجع عموما به صورت افقی از چپ به راست ترسیم می‌شود. از مقالات مقاومت‌ها و خازن‌ها می‌دانیم که جریان و ولتاژ در مدار AC مقاومتی هر دو «هم فاز» هستند و بنابراین بردار،  VR روی جریان یا خط مرجع رسم می‌شود.

همچنین از بالا می‌دانیم که جریان در یک مدار کاملا سلفی از ولتاژ عقب می‌افتد و بنابراین بردار VL 90 درجه جلوتر از جریان و به همان اندازه VR رسم می‌شود و این در زیر نشان داده شده است.

مدار AC اتصال سری LR

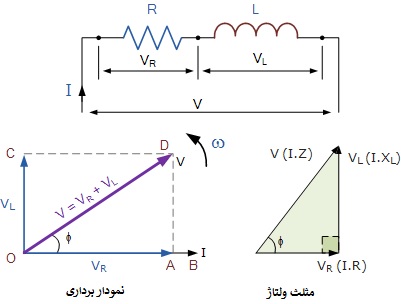4) مدار AC اتصال سری LR

در نمودار برداری بالا می‌توان دید که خط OB نشان دهنده خط مرجع جریان است، خط OA ولتاژ مولفه مقاومتی است که با جریان هم فاز است. خط OC ولتاژ سلفی را نشان می‌دهد که 90 درجه جلوتر از جریان است، بنابراین می‌توان دید که جریان 90 درجه از ولتاژ عقب می‌افتد. خط OD ولتاژ حاصل یا منبع تغذیه در مدار را به ما می‌دهد. مثلث ولتاژ از قضیه فیثاغورث گرفته شده و به صورت زیر ارائه می‌شود:

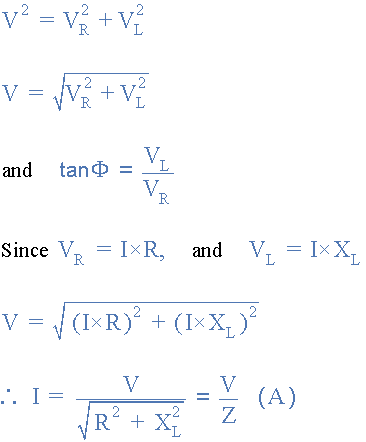
در مدار DC به نسبت ولتاژ به جریان مقاومت می‌گویند. با این حال، در یک مدار AC این نسبت به عنوان امپدانس Z با واحد اهم شناخته می‌شود. امپدانس کل مقاومت در برابر عبور جریان در یک «مدار AC» است که حاوی مقاومت و راکتانس سلفی است. اگر اضلاع مثلث ولتاژ بالا را بر جریان تقسیم کنیم، مثلث دیگری به دست می آید که اضلاع آن نشان‌دهنده مقاومت، راکتانس و امپدانس سیم‌پیچ است. این مثلث جدید «مثلث امپدانس» نامیده می‌شود.

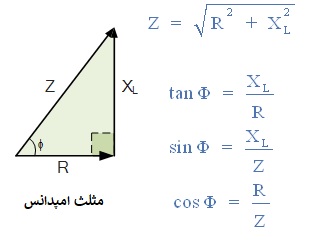5) مثلث امپدانس

مثال ۲) راکتانس سلفی
یک سیم‌پیچ سلونویید مقاومت ۳۰ اهمی و اندوکتانس ۵/۰ هانری دارد. اگر جریان عبوری از سیم‌پیچ برابر با ۴ آمپر باشد، محاسبه کنید:

الف) ولتاژ منبع تغذیه اگر فرکانس برابر با ۵۰ هرتز باشد:

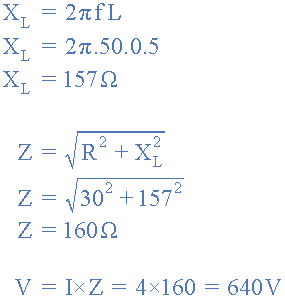
ب) زاویه فاز بین ولتاژ و جریان را بیابید

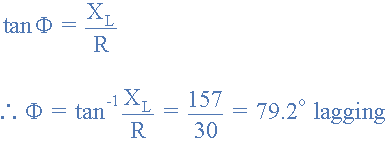
مثلث توان یک سلف AC
یک نوع دیگر از پیکربندی مثلث وجود دارد که می‌توانیم برای یک مدار سلفی از آن استفاده کنیم و آن «مثلث توان» است. توان در یک مدار سلفی به عنوان توان راکتیو یا ولت آمپر راکتیو شناخته می‌شود، نماد Var که با ولت آمپر اندازه‌گیری می‌شود. در مدارهای AC سری RL، جریان با زاویه Φo از ولتاژ تغذیه عقب می‌افتد. در یک مدار AC سلفی خالص، جریان به میزان 90 درجه نسبت به ولتاژ منبع تغذیه خارج از فاز خواهد بود. به این ترتیب، کل توان راکتیو مصرف‌شده توسط سیم‌پیچ برابر با صفر خواهد بود زیرا هر توان مصرفی توسط توان نیرو محرکه خودالقایی تولید شده خنثی می‌شود. به عبارت دیگر، توان خالص بر حسب وات مصرف شده توسط یک سلف خالص در پایان یک چرخه کامل صفر است، زیرا انرژی هم از منبع تغذیه گرفته شده و هم به آن باز می‌گردد.

توان راکتیو (Q) یک سیم‌پیچ را می‌توان به صورت I۲ x XL ) مشابه I۲R در مدار (DC ارائه کرد. پس سه ضلع یک مثلث توان در مدار AC با توان ظاهری (S)، توان واقعی (P) و توان راکتیو (Q) نشان داده می‌شود.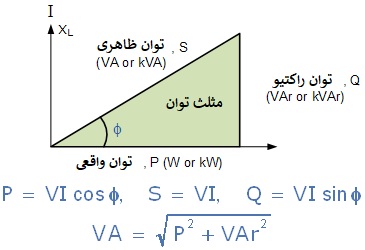6) مثلث توان