راکتانس القایی

میزان مقاومت جریان عبوری از یک سلف AC را، راکتانس القایی (Inductive Reactance) می‌نامند که به‌ صورت خطی به فرکانس منبع تغذیه وابسته است.

سلف‌ها  و چوک‌ها، در واقع سیم‌پیچ یا حلقه‌های سیمی می‌باشند؛ که یا در اطراف  لوله‌ی توخالی (هسته هوا) و یا در اطراف برخی از مواد فرومغناطیسی (هسته  آهن) پیچیده می‌شوند تا مقدار خاصیت القایی آن‌ها، افزایش یابد که در این  صورت اندوکتانس نامیده می‌شوند.

سلف‌ها، انرژی خود  را در قالب یک میدان مغناطیسی ذخیره می‌کنند؛ که با اعمال ولتاژ به پایانه  (ترمینال) های یک سلف ایجاد می‌شود. رشد جریان، در زمانی که از سلف عبور  می‌کند، در همان لحظه رخ نمی‌دهد؛ بلکه توسط خودالقاها یا مقدار emf معکوس  (نیروی محرکه الکتریکی معکوس شده) تعیین می‌شود. درنتیجه، برای یک سیم‌پیچ  القایی، این ولتاژ emf  معکوس (VL)، متناسب با سرعت تغییر جریان جاری در آن است.

این  جریان، تا زمانی افزایش می‌یابد؛ که به حداکثر حالت مانای خود، که در حدود  5 ثابت زمانی است، برسد؛ یعنی تا زمانی که این emf معکوس القاشده توسط خود  سلف، تا صفر کاهش یابد. در این مرحله، جریان حالت مانا در یک سیم‌پیچ جاری  است و دیگر هیچ emf معکوسی، برای مخالفت با جریان جاری القا نمی‌گردد و  بنابراین سیم‌پیچ، بیشتر به صورت یک اتصال کوتاه، عمل نموده و اجازه می‌دهد  که حداکثر جریان، از آن عبور کند.

با این‌حال، در یک مدار جریان متناوب، که حاوی اندوکتانس AC می‌باشد؛ جریان جاری در یک سلف، بسیار متفاوت از ولتاژ DC حالت مانا،  رفتار می‌کند. اکنون، در یک مدار AC، میزان مخالفت جریان جاری در سیم‌ پیچ‌  های کویل، نه‌تنها به اندوکتانس کویل، بلکه به فرکانس شکل‌ موج ولتاژ  اعمال‌شده نیز بستگی دارد؛ درحالی‌که از مقادیر مثبت به منفی در تغییر است.

میزان  مخالفت واقعی جریان جاری در یک کویل مدار AC؛ توسط مقاومت AC کویل تعیین  می‌گردد؛ که با یک عدد مختلط نشان داده می‌شود. اما برای تشخیص مقدار  مقاومت DC، از مقدار مقاومت AC ،که عنوان امپدانس نیز شناخته می‌شود؛ از عبارت راکتانس استفاده می‌کنند.

همانند  مقاومت، راکتانس نیز برحسب اهم محاسبه می‌گردد اما از نماد “X” برای آن  استفاده می‌گردد؛ تا از مقدار مقاومت خالص “R” قابل تمایز باشد و از  آن‌جایی، که عنصر مورد بررسی سلف است؛ راکتانس یک سلف، راکتانس القایی ( XL ) نامیده می‌شود که بر حسب اهم اندازه‌گیری می‌گردد. مقدار آن را می‌توان توسط فرمول زیر به دست آورد.

راکتانس القایی

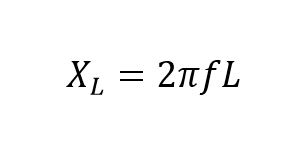
که در آن:

  XL      …   راکتانس القایی برحسب اهم (Ω) است.

  π (pi) …   ثابت عددی برابر با ۳.۱۴۲ است.

   ƒ    …     فرکانس برحسب هرتز (Hz) است.

   L    …     اندوکتانس برحسب هنری (H) است.

ما هم‌چنین، می‌توانیم راکتانس القایی را بر حسب رادیان، در جایی که ω برابر با ۲πf است؛ تعریف کنیم.

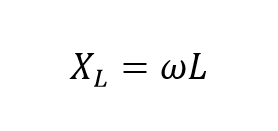
بنابراین، هنگامی‌که، یک ولتاژ سینوسی به یک کویل القایی اعمال می‌گردد؛ emf معکوس، با افت و خیز جریان جاری در کویل مخالفت می‌کند، در یک کویل کاملا  القایی که مقاومت یا تلفات صفر دارد؛ این امپدانس (که می‌تواند یک عدد  مختلط باشد) برابر با راکتانس القایی است. هم‌چنین، راکتانس توسط بردار،  نمایش داده می‌شود؛ زیرا هم دارای اندازه و هم جهت (زاویه) است. مدار زیر  را در نظر بگیرید.

اندوکتانس AC با منبع سینوسی

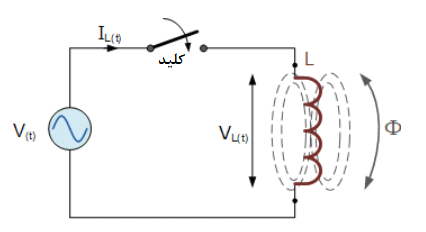1. اندوکتانس AC با منبع سینوسی

این مدار ساده در بالا، که از یک راکتانس خالص (L) برحسب هنری تشکیل شده‌است؛ به یک ولتاژ سینوسی متصل گشته است که با عبارت V(t) = Vmax sinωt نمایش داده می‌شود. زمانی‌که کلید بسته می‌شود؛ این ولتاژ سینوسی، سبب  می‌شود تا جریان، جاری گردد و از صفر تا مقدار حداکثر خود، خیز یابد. این  خیز یا تغییر در جریان، سبب القای میدان مغناطیسی درون کویل می‌شود؛ که به  نوبه‌ی خود با این تغییر جریان مخالفت نموده یا سبب محدود شدن آن می‌گردد.

اما  قبل از این‌که، جریان فرصت این را یابد که به حداکثر مقدار خود، مانند  حالتی که در مدار DC طی می‌کند، برسد؛ ولتاژ پلاریته (قطبیت) خود را تغییر  می‌دهد و سبب تغییر جهت جریان می‌شود. این تغییر به یک جهت دیگر، یک‌بار  دیگر، توسط emf خودالقایی معکوس، به تاخیر می‌افتد و در یک مدار حاوی اندوکتانس خالص، سبب تاخیر °۹۰ جریان می‌شود.

ولتاژ اعمالی، به حداکثر مقدار مثبت خود که ربع (1/4f) یک سیکل است؛ زودتر از زمانی می‌رسد که جریان به حداکثر مقدار مثبت خود  می‌رسد؛ به بیان دیگر؛ ولتاژ اعمال شده به یک مدار کاملا القایی، “پیشرو”تر  از جریان، به اندازه ربع یک سیکل یا °۹۰ خواهد بود، که در زیر آورده شده است.

شکل‌ موج سینوسی برای اندوکتانس AC

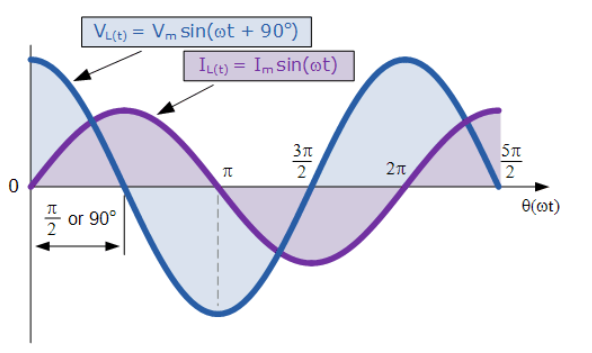2. شکل‌ موج سینوسی برای اندوکتانس AC

این اثر را می‌توان، با یک نمودار فازوری در یک مدار القایی خالص، نشان داد؛ که ولتاژ °۹۰ از جریان، “پیشرو”تر است و  این درحالی است که ولتاژ به عنوان مرجع در نظر گرفته‌شود. ما هم‌چنین،  می‌توانیم بگوییم که جریان به اندازه ربع  یک سیکل یا °۹۰، “عقب‌مانده” از ولتاژ است که در نمودار زیر نشان داده شده‌است.

نمودار فازوری برای اندوکتانس AC

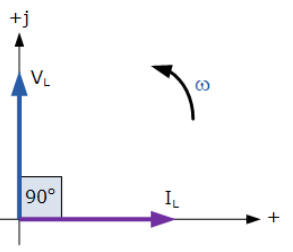3. نمودار فازوری برای اندوکتانس AC

بنابراین، برای یک سلف بدون تلفات خالص، ، ° ۹۰ پیشرو تر از  خواهد بود یا می‌توان گفت، که ، °۹۰، “عقب‌مانده”‌تر از  است.

راه‌های  متفاوت بسیاری، برای به‌خاطرسپردن رابطه فاز میان ولتاژ و جریان جاری، در  یک مدار القایی خالص وجود دارد؛ اما یکی از روش‌های بسیار ساده و آسان برای  آن، استفاده از اصطلاح حفظی ELI است (مانند نام دختران (Ellie)تلفظ می‌شود).  ELI مخفف عبارت Electromotive force first (ابتدا نیروی محرکه الکتریکی) در یک اندوکتانس AC است؛ که یعنی L (سلف) قبل از جریان (I) می آید. به عبارت‌دیگر، ولتاژ قبل از جریان در سلف است؛ که سبب ترتیب E،L و I شده که برابر با ELI است. ولتاژ در هر زاویه‌ی فازی که شروع می‌شود؛ این عبارت، همیشه برای یک مدار سلفی خالص صادق است.

اثر فرکانس بر راکتانس القایی

زمانی‌که، یک منبع 50 هرتز، به یک اندوکتانس AC مناسب متصل گردد؛  جریان °90 تاخیر خواهد داشت؛ که پیش از این بیان شد و مقدار پیک جریان بر  حسب آمپر را، قبل از آن‌که ولتاژ قطبیت را در آخر نیم‌سیکل معکوس کند؛ بدست  می آورد ؛یعنی جریان به مقدار حداکثر خود در” T ثانیه” می‌رسد.

اما  اگر اکنون، یک منبع 100 هرتز از همان ولتاژ پیک را به کویل اعمال کنیم؛  جریان هم‌چنان °90  تاخیر خواهد داشت. اما حداکثر مقدار آن کمتر از 50 هرتز  خواهد بود؛ زیرا زمان موردنیاز برای رسیدن به حداکثر مقدار خود، به دلیل  افزایش فرکانس، کاهش یافته‌است و فقط ” 1/2 T  ثانیه” دارد تا به حداکثر  مقدار خود برسد. هم‌چنین، نرخ تغییر شار درون کویل نیز، به دلیل افزایش  فرکانس، افزایش یافته است.

از معادله فوق برای راکتانس القایی، می‌توان دید؛ که اگر فرکانس یا اندوکتانس افزایش یابند؛ مقدار کلی راکتانس القایی‌کویل نیز افزایش می‌یابد.  زمانی‌که، فرکانس افزایش می‌یابد و به بی‌نهایت میل ‌می‌کند؛ راکتانس  سلف‌ها و درنتیجه، امپدانس آن‌ها به سمت بی‌نهایت میل کرده که مانند یک  مدار باز عمل می‌کند.

به همین‌ترتیب، با نزدیک‌شدن فرکانس به صفر یا  DC، راکتانس سلف‌ها نیز تا به صفر کاهش می‌یابند و مانند یک اتصال کوتاه  عمل می‌کنند. این بدین معنی است که راکتانس القایی، “مستقیما با فرکانس  متناسب است” و در فرکانس‌های کم، مقدار کم و در فرکانس‌های بالا، مقدار  بیشتری دارد؛ که در زیر آورده شده است.

راکتانس القایی در مقابل فرکانس

راکتانس القایی یک سلف، با افزایش فرکانس در آن افزایش می‌یابد؛ بنابراین، راکتانس القایی متناسب با فرکانس است( XL α ƒ) زیرا emf معکوس تولید‌ شده در سلف برابر با اندوکتانس ضرب‌شده در نرخ  تغییر جریان در سلف است. هم‌چنین، با افزایش فرکانس، جریان عبوری از سلف  نیز، کاهش می‌یابد.

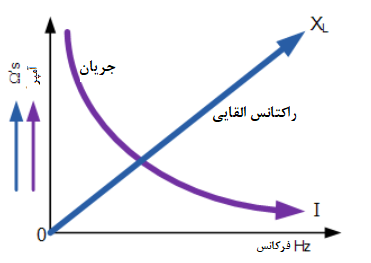۴. اثر فرکانس بر راکتانس

می‌توان، اثر فرکانس‌های بسیار کم و بسیار زیاد را بر راکتانس یک اندوکتانس AC خالص به شرح زیر ارائه داد:

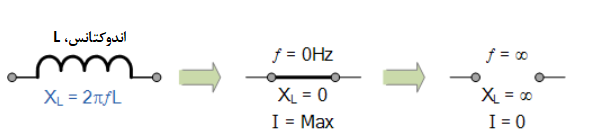
در مدار AC، حاوی اندوکتانس خالص، فرمول زیر اعمال می‌گردد:

برای یافتن چگونگی رسیدن به این معادله، باید گفت؛ emf خودالقا  در سلف توسط قانون فارادی تعیین می‌شود، که “اثر خودالقایی” را ایجاد  می‌کند. هنگامی‌که، یک جریان از یک سیم‌ پیچ القایی عبور می‌کند؛ نرخ تغییر  جریان AC، باعث ایجاد یک emf در همان کویل می‌شود که جریان متغیر  را خنثی می‌کند. این اثر بر روی کویل، در جایی‌که، میدان مغناطیسی که خود  که در اثر جریان جاری در آن ایجاد شده‌است؛ با هرگونه تغییر جریان مخالفت  می‌نماید، “خودالقایی” نامیده می‌شود.

حداکثر مقدار ولتاژ این emf  خودالقایی، با حداکثر نرخ تغییر جریان با این مقدار ولتاژ در کویل مطابقت  دارد که به صورت زیر آورده شده است:

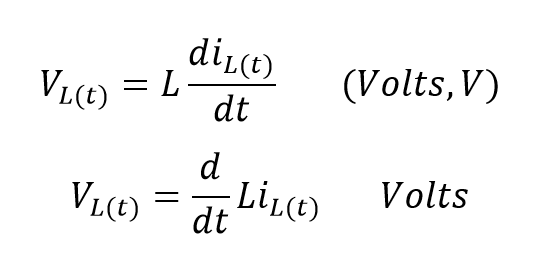
در جایی‌که، d/dt نرخ تغییر جریان را در زمان، نشان می‌دهد.

جریان سینوسی جاری در یک کویل القایی (L) که سبب ایجاد شار مغناطیسی اطراف آن می‌شود، به صورت زیر ارائه می‌شود:

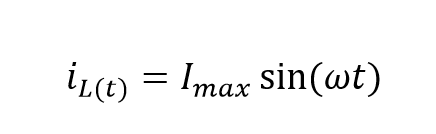
درنتیجه، معادله بالا را به صورت زیر، می‌توان دوباره نوشت:

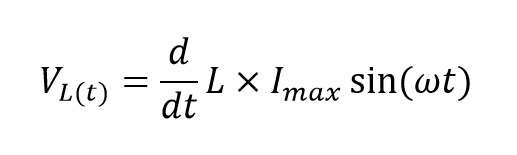
مشتق گرفتن از جریان سینوسی به ما می‌دهد:

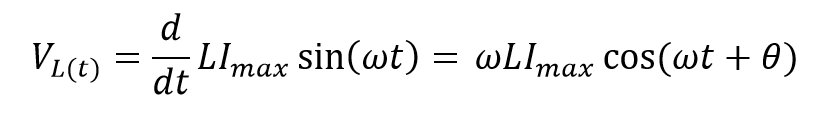
هویت مثلثاتی  بیان می‌کند؛ که یک شکل‌ موج کسینوسی به طور موثر،  یک شکل‌ موج سینوسی را °۹۰+ شیفت داده است. درنتیجه، می‌توان معادله‌ی فوق  را به صورت موج سینوسی دوباره نوشت؛ تا ولتاژ در یک اندوکتانس AC به صورت زیر تعریف شود:

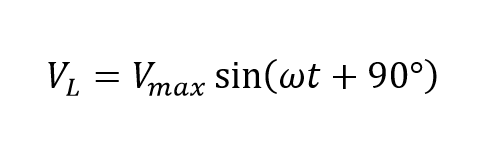
در این‌جا، VMAX = ωLIMAX = √۲VRMS است؛ که حداکثر دامنه ولتاژ می‌باشد و اختلاف فاز یا زاویه فاز میان شکل‌ موج‌های جریان و ولتاژ، برابر با θ = + ۹۰o است. این جریانی است که با زاویه °۹۰ از ولتاژ در یک سلف خالص، عقب‌تر مانده است.

 حوزه‌ی فازور

در حوزه فازور، ولتاژ کویل به صورت زیر آورده می‌شود:

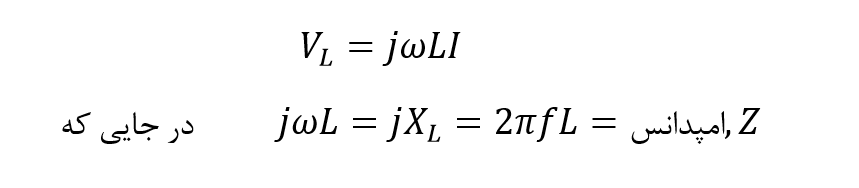
و فرم قطبی را می‌توان نوشت:  XL∠۹۰o در جایی‌که:

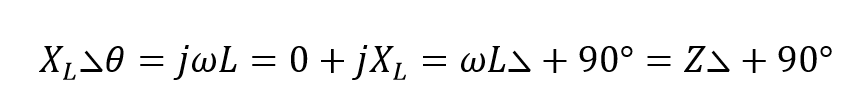
AC در مدار سری R+L

در بالا مشاهده شد؛ که جریان جاری در یک کویل القایی خالص، از  ولتاژ با زاویه °۹۰ عقب می‌ماند و منظور از یک سیم‌پیچ القایی خالص، کویلی  است که هیچ مقاومت اهمی نداشته و بنابراین تلفات I۲R ندارد. اما در دنیای واقعی، امکان داشتن یک اندوکتانس AC خالص، وجود ندارد.

تمام  کویل‌های الکتریکی، رله‌ها، سلونوئیدها و ترانسفورماتورها، هر اندازه هم  که در پیچ‌های کویل مورد استفاده قرار بگیرند، مقاومت مشخصی خواهند داشت.  این امر، به این دلیل است که سیم مسی مقاومت دارد. در نتیجه، می‌توانیم در  نظر بگیریم، که کویل القایی ما، اگر دارای مقاومت باشد، یک مقاومت (R) سری  با اندوکتانس (L) خواهد بود که می‌توان آن را “اندوکتانس ناخالص” نامید.

اگر کویل، دارای مقداری مقاومت “داخلی” باشد؛ ما باید امپدانس کلی کویل را، به صورت مقاومت سری با اندوکتانس در یک مدار AC، که حاوی هم اندوکتانس (L) و هم مقاومت (R) است؛ نشان دهیم. V در کل این ترکیب، فازور حاصل دو مولفه ولتاژ  VR و VL  است.

این بدین معناست، که جریان عبوری از کویل، هم‌چنان از ولتاژ عقب می‌ماند؛ اما بسته به مقادیر  و  VR  و VL در واقع مجموع فازور، مقدار آن از °90 کمتر خواهد بود. زاویه‌ی جدید بین  شکل‌موج‌های ولتاژ و جریان، اختلاف فازی را در اختیار ما قرار می‌دهد، که  ما با زاویه فاز مدار که با نماد یونانی phi(φ) نشان داده می‌شود؛  می‌شناسیم.

مدار زیر را در نظر بگیرید؛ در جایی‌که، مقاومت القایی غیرخالص (R) به صورت سری به اندوکتانس خالص (L) متصل شده‌است.

مدار سری مقاومتی- اندوکتانسی

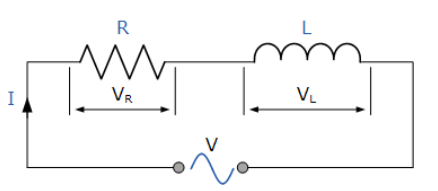۵. مدار سری مقاومتی-اندوکتانسی

در مدار سری RL بالا، می‌توان دید که جریان بین مقاومت و اندوکتانس مشترک است؛ در حالی‌که ولتاژ از دو مولفه VR  و VL ساخته می‌شود. ولتاژ حاصل از این دو جز را می‌توان به صورت ریاضیاتی یا با  ترسیم نمودار یافت. برای ایجاد نمودار برداری باید یک مولفه‌ی مشترک یا  مرجع یافت‌شود و در یک مدار AC سری، جریان، منبع مرجع می‌باشد؛ زیرا این  جریان هم در مقاومت و هم در اندوکتانس جاری است. نمودارهای برداری منفرد  برای یک مقاومت خالص و یک اندوکتانس خالص به صورت زیر است:

نمودارهای برداری برای دو عنصر خالص

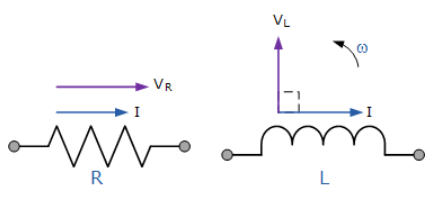۶. نمودارهای برداری برای دو عنصر خالص

از بالا و از مقاله های قبلی در مورد مقاومت AC، دریافتیم که ولتاژ و جریان در یک مدار مقاومتی، هر دو هم‌فاز بوده و از این رو از نظر مقیاس‌گذاری، بردار ولتاژ VR ،بر بردار جریان IR سوار می‌شود. هم‌چنین از بالا متوجه شدیم که جریان در یک مدار اندوکتانسی AC (خالص) از ولتاژ عقب می‌ماند؛ از این‌رو، بردار VL با ° 90 اختلاف زاویه با جریان، که در یک مقیاس و راستا با VR است، رسم شده‌است.

نمودار برداری ولتاژ حاصل

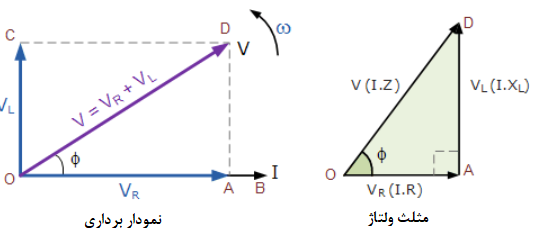۷. نمودار برداری ولتاژ حاصل

از نمودار بالا می‌توانیم ببینیم؛ که خط OB، مرجع جریان افقی بوده و خط OA، ولتاژ  روی مولفه‌ی مقاومتی است که هم‌فاز با جریان است. خط OC، ولتاژ القایی را  نشان می‌دهد؛ که °90 با جریان اختلاف زاویه دارد و بنابراین به خوبی دیده  می‌شود؛ که جریان، از ولتاژ القایی خالص، °90 عقب می‌ماند. خط OD، ولتاژ  تغذیه حاصل را به ما میدهد، درنتیجه:

V  برابر است با مقدار r.m.s ولتاژ اعمال‌شده

I برابر است با مقدار r.m.s جریان سری شده

VR برابر است با افت ولتاژ I.R دو سر مقاومت که با جریان، هم‌فاز است.

VL برابر است با افت ولتاژ I.XL دو سر اندوکتانس که از جریان° ۹۰ پیشروی می‌کند.

از  آن‌جایی که، جریان، در یک اندوکتانس خالص دقیقا، °90 از ولتاژ عقب‌تر  می‌ماند؛ نمودار فازوری حاصل از یک ولتاژ منفرد، به دو مولفه VR و  VL تقسیم می‌شود؛ که نشان‌دهنده‌ی یک مثلث زاویه‌دار قائمه است که در بالا با  نماد OAD نشان داده شده‌است. سپس می‌توانیم از قضیه فیثاغورث استفاده  نماییم تا مقدار ولتاژ حاصل از مدار مقاومت/ سلف (RL) را به صورت ریاضی  پیدا کنیم.

از آنجایی‌که  VR = I.R  و VL = I.XL است؛ ولتاژ اعمال‌شده، مجموع این دو بردار به شرح زیر خواهد بود:

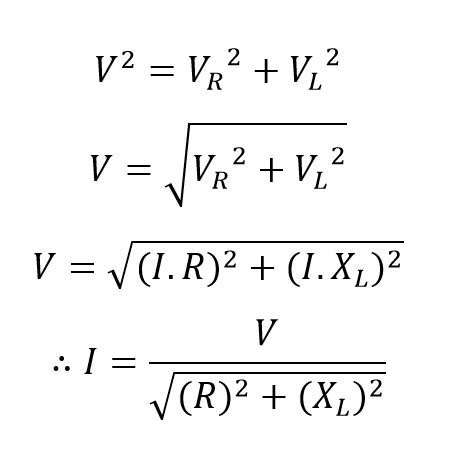
اندازه   نشان‌دهنده‌ی امپدانس Z در یک مدار است.

امپدانس یک راکتانس AC

امپدانس Z، میزان مخالفت ” کامل” جریان جاری در یک مدار  AC است؛ که از مقاومت (بخش حقیقی) و راکتانس (بخش موهومی) تشکیل شده‌ است.  امپدانس هم‌چنین دارای واحد اهم (Ω) است. امپدانس به فرکانس (ω) مدار  بستگی دارد؛ زیرا این امر بر تمام عناصر راکتیو مدار اثر می‌گذارد و در یک  مدار سری، تمام امپدانس‌های مقاومتی و راکتیو با یک‌دیگر جمع می‌شوند.

امپدانس هم‌چنین، می‌تواند با عدد مختلط Z = R + jXL نشان  داده شود؛ اما یک فازور نیست، بلکه نتیجه‌ی دو یا چند فازور است که باهم  ترکیب شده‌اند. اگر اضلاع مثلث ولتاژ بالا را بر I تقسیم کنیم؛ یک مثلث  دیگر به دست می‌آید که اضلاع آن، مقاومت، راکتانس و امپدانس مدار را به  صورت زیر نشان می‌دهد:

مثلث امپدانس RL

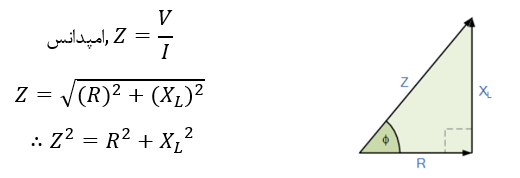8. مثلث امپدانس RL

                                      در نتیجه :

درجایی‌که j، نشان‌دهنده‌ی ° 90 شیفت فاز است.

این، بدین معنی است، که زاویه فاز مثبت(θ) بین ولتاژ و جریان به صورت زیر خواهد بود:

زاویه فاز

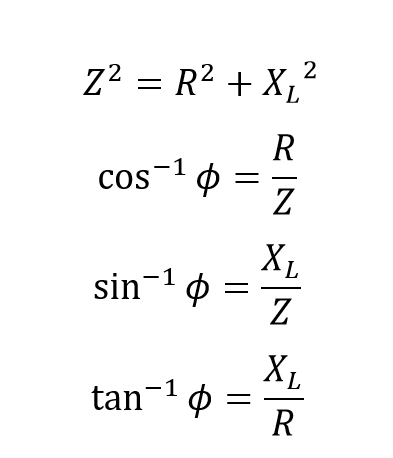
درحالی‌که، مثال ما در بالا، نشان‌دهنده‌ی یک اندوکتانس AC ساده  غیرخالص است؛ اگر دو یا چند سیم‌پیچ القایی به صورت سری، به هم متصل شوند؛  یا یک سیم‌ پیچ منفرد، به صورت سری به مقاومت‌های غیر القایی زیادی اتصال  یابد؛ آنگاه مقاومت کل برای عناصر مقاومتی برابر با …+R۱ + R۲ + R۳  خواهد بود؛ که مقدار مقاومت کل مدار را به ما می‌دهد.

به همین‌ترتیب، راکتانس کلی عناصر القایی مدار برابر با …+X۱ + X۲ + X۳ خواهد  بود؛ که مقدار راکتانس کلی مدار را در اختیار ما قرار می‌دهد. پس، یک مدار  حاوی چوک‌ها،کویل‌ها و مقاومت‌های مختلف می‌تواند به راحتی تا مقدار  امپدانس کاهش یابد. Z متشکل از یک مقاومت منفرد سری شده با یک راکتانس  منفرد رابطه Z۲ = R۲ + X۲ را خواهد داشت.

مثال شماره 1 - راکتانس AC

در مدار زیر، ولتاژ تغذیه به صورت روبرو تعریف شده‌است: V(t) = 325 sin( 314t – 30o ) و  L = 2.2H است. مقدار rms جریان عبوری از کویل را محاسبه نموده و نمودار فازوری حاصل را رسم کنید.

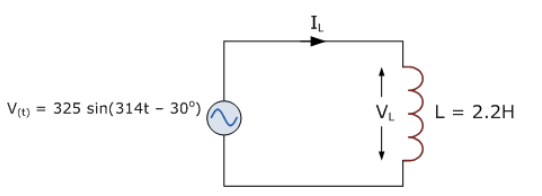9. راکتانس ac - مثال 1

ولتاژ rms در کویل، همان ولتاژ تغذیه خواهد بود. اگر حداکثر  ولتاژ منبع تغذیه 325 ولت باشد، مقدار rms معادل 230 ولت خواهد بود. تبدیل  این مقدار در حوزه زمان به فرم قطبی به ما می‌دهد:  VL = ۲۳۰ ∠-۳۰o (volts). راکتانس القایی کویل نیز برابر با XL = ωL = 314 x 2.2 = 690Ω خواهد بود. در نتیجه، جریان عبوری از کویل که توسط قانون اهم محاسبه می‌شود، خواهد بود:

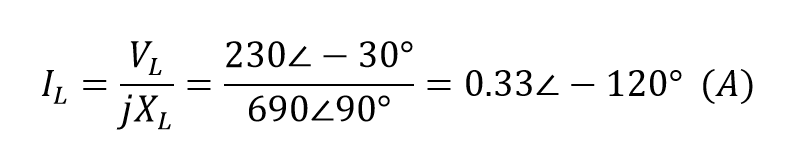
با °۹۰ عقب‌ماندگی جریان از ولتاژ، نمودار فازوری خواهد بود:

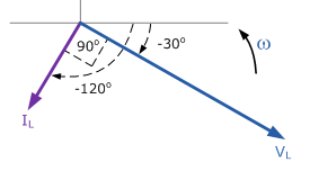۱۰. نمودار فازوری- مثال ۱

مثال شماره 2 - راکتانس AC

یک کویل، دارای مقاومت 50Ω و اندوکتانس 0.5H است. اگر جریان  عبوری از کویل 4 آمپر باشد؛ مقدار rms ولتاژ چه مقدار خواهد بود؟ اگر  فرکانس برابر با 50Hz باشد.

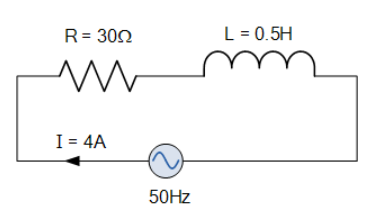11. راکتانس ac - مثال 2

امپدانس مدار خواهد بود:

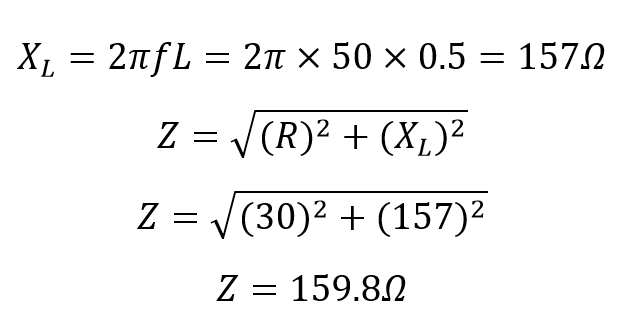
افت ولتاژ دو سر هر عنصر به صورت زیر بدست می آید:

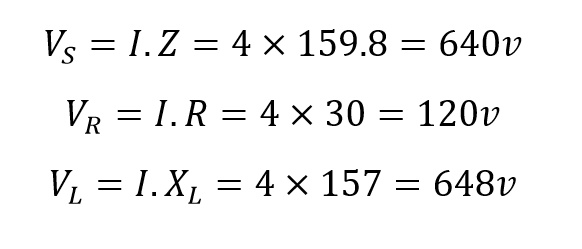
زاویه‌ی فاز بین جریان و ولتاژ به صورت زیر محاسبه می‌شود:

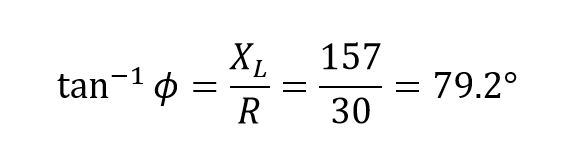
نمودار فازور خواهد بود:

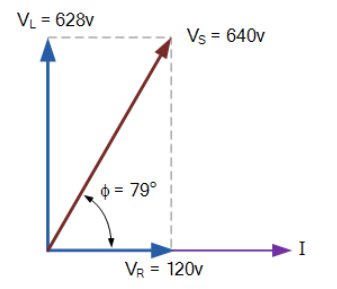۱۲. نمودار فازور - مثال ۲

در مقاله بعدی، در مورد ظرفیت خازنی AC، به رابطه‌ی ولتاژ – جریان یک خازن،  زمانی‌که یک شکل‌ موج سینوسی حالت مانا به آن اعمال می‌شود؛ به همراه  نمایش نمودار فازوری آن برای خازن خالص و ناخالص، خواهیم پرداخت.