زمانی که هر پایه‌ی سلف به صورت جداگانه به پایه‌های سلف یا سلف‌های دیگر متصل شده باشد، گفته میشود که اتصال موازی دارد. افت ولتاژ دو سر سلف‌ها با اتصال موازی یکسان خواهد بود. پس سلف‌های موازی دارای یک ولتاژ مشترک در دوسر خود هستند و در مثال ما در زیر، ولتاژ دو سر سلف‌ها به صورت زیر آورده شده است:
VL1 = VL2 = VL3 = VAB …etc
در شکل بعدی تمامی سلف‌های L۱، L۲ و L۳ بین دو نقطه A و B به صورت موازی بسته شده‌اند:
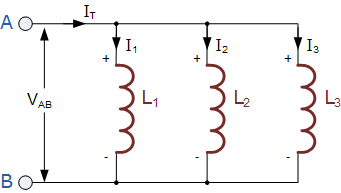۱. مدار اتصال موازی سلف‌ها
در مقاله قبلی سلف‌ها متوجه شدیم که اندوکتانس کل LT مدار برابر با مجموع اندوکتانس سلف‌های مجزا است. برای سلف‌های موازی، اندوکتانس مدار معادل LT متفاوت محاسبه میشود. مجموع جریان‌های منفرد که از هر سلف عبور می‌کند را می‌توان با استفاده از قانون جریان کرشهف (KCL) پیدا کرد که در آن، IT = I۱ + I۲ + I۳ و ما از آموزش‌های قبلی در مورد اندوکتانس می‌دانیم که نیروی محرکه خود القا‌شده در یک سلف به صورت V = L di/dt محاسبه میشود. پس با در نظر گرفتن مقادیر جریان‌های جداگانه‌ای که از هر سلف در مدار ما در بالا می‌گذرد، و جایگزینی جریان i به جای i۱ + i۲ + i۳ ولتاژ در سراسر ترکیب موازی به صورت زیر داده میشود:
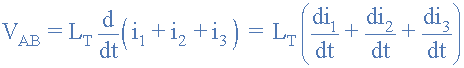
با جایگزینی di/dt با V/L در فرمول بالا خواهیم داشت:
می‌توانیم آن را ساده کنیم تا یک عبارت نهایی برای محاسبه اندوکتانس کل یک مدار در هنگام اتصال سلف‌ها به صورت موازی ارائه دهیم و این به صورت زیر است:
معادله سلف موازی
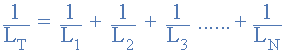
در اینجا، مانند محاسبات برای مقاومت‌های موازی، مقدار معکوس (1/Ln) سلف‌های منفرد به‌جای خود سلف‌ها با هم جمع می‌شوند. اما باز هم مانند اتصال سری سلف‌ها، معادله بالا فقط زمانی صادق است که بین دو یا چند سلف، «هیچ» اندوکتانس متقابل یا کوپلینگ مغناطیسی وجود نداشته باشد (آنها از نظر مغناطیسی از یکدیگر ایزوله شده باشند). در جایی که بین سیم‌پیچ‌ها کوپلینگ وجود دارد، اندوکتانس کل نیز تحت تاثیر مقدار کوپلینگ قرار می‌گیرد.
این روش محاسبه را می‌توان برای محاسبه هر تعداد اندوکتانس مجزا که در یک شبکه موازی به هم متصل شده‌اند، استفاده کرد. با این حال، اگر تنها دو سلف جداگانه به صورت موازی وجود داشته باشد، می‌توان از فرمول بسیار ساده‌تر و سریع‌تری برای یافتن مقدار اندوکتانس کل استفاده کرد و این عبارت است از:
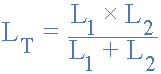
یک نکته مهم در مورد سلف‌ها در مدارهای موازی این است که اندوکتانس کل (LT) دو یا چند سلف که به طور موازی به یکدیگر متصل شده‌اند، همیشه کمتر از مقدار کوچکترین اندوکتانس در زنجیره موازی خواهد بود.
مثال 1) اتصال موازی سلف‌ها
سه سلف ۶۰، ۱۲۰ و ۷۵ میلی‌هانری در یک ترکیب موازی و بدون اندوکتانس متقابل متصل شده‌اند. اندوکتانس کل ترکیب موازی را بر حسب میلی‌هانری محاسبه کنید.
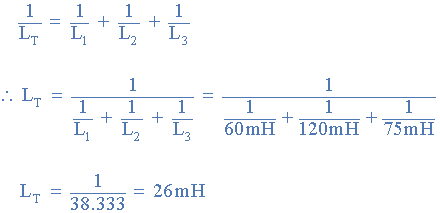
اتصال موازی سلف‌های دارای اندوکتانس متقابل
هنگامی که سلف‌ها به طور موازی به یکدیگر متصل می‌شوند به طوری که میدان مغناطیسی یکی با دیگری پیوند می‌یابد، اثر اندوکتانس متقابل بسته به مقدار کوپلینگ مغناطیسی که بین سیم‌پیچ‌ها وجود دارد، موجب افزایش یا کاهش اندوکتانس کل میشود. اثر این اندوکتانس متقابل به فاصله سیم‌پیچ‌ها و جهت‌گیری آنها نسبت به یکدیگر بستگی دارد. سلف‌های موازی دارای اندوکتانس متقابل را می‌توان به‌عنوان «کمک‌کننده» یا «مخالف» با اندوکتانس کل طبقه‌بندی کرد که در مقایسه با سیم‌پیچ‌هایی که اندوکتانس متقابل صفر دارند، سیم‌پیچ‌های متصل کمکی موازی، باعث افزایش اندوکتانس معادل کل و سیم‌پیچ‌های متصل مخالف موازی باعث کاهش اندوکتانس معادل کل می‌شوند. سیم‌پیچ‌های موازی دارای اندوکتانس متقابل را می‌توان با استفاده از نقاط یا نشانگرهای پلاریته مانند شکل زیر به صورت متصل به هم در یک پیکربندی کمکی یا مخالف نشان داد.
2) سلف‌های موازی کمک‌کننده
ولتاژ دو سلف کمکی موازی بالا باید برابر باشد زیرا آنها موازی هستند، بنابراین دو جریان i۱ و i۲ باید تغییر کنند تا ولتاژ دو طرف آنها ثابت بماند. پس اندوکتانس کل، LT برای دو سلف کمکی موازی به صورت زیر به دست می‌آید:
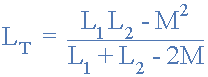
که در معادله بالا 2M نشان‌دهنده تاثیر سیم‌پیچ L۱ بر L۲ و به همین ترتیب سیم‌پیچ L۲ بر L۱ است.
اگر دو سلف مساوی باشند و کوپلینگ مغناطیسی مانند مدار حلقوی کامل باشد، اندوکتانس معادل دو سلف به صورت موازی به صورت LT = L۱ = L۲ = M است. اما اگر اندوکتانس متقابل بین آنها صفر باشد، اندوکتانس معادل برابر با L ÷ 2 مانند دو سلف خودالقای موازی خواهد بود.
اگر یکی از دو سیم‌پیچ نسبت به دیگری معکوس شود، آنگاه دو سلف موازی مخالف خواهیم داشت و اندوکتانس متقابل M که بین دو سیم‌پیچ وجود دارد، به جای اثر کمکی همانطور که در زیر نشان داده شده است، یک اثر مخالف روی هر سیم‌پیچ خواهد داشت.
سلف های موازی مخالف
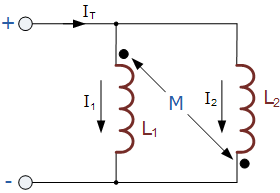3) سلف‌های موازی مخالف
پس اندوکتانس کل LT برای سلف‌های موازی مخالف به صورت زیر خواهد بود:
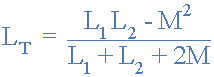
این بار، اگر دو سلف از نظر ارزش برابر باشند و کوپلینگ مغناطیسی بین آنها کامل باشد، اندوکتانس معادل و همچنین نیروی محرکه خودالقا شده در سرتاسر سلف ها صفر خواهد شد زیرا دو سلف یکدیگر را خنثی می‌کنند.
این به این دلیل است که از آنجایی که دو جریان، i۱ و i۲ از هر سلف عبور می‌کنند، به نوبه خود کل شار متقابل ایجاد شده بین آنها صفر است، زیرا دو شار تولید شده توسط هر سلف، هر دو از نظر دامنه مساوی اما در جهت مخالف هستند.
پس دو سیم‌پیچ به طور موثر به یک اتصال کوتاه برای عبور جریان در مدار تبدیل می‌شوند بنابراین اندوکتانس معادل LT برابر با (L ± M) ÷ 2 میشود.
مثال 2) اتصال موازی سلف‌ها
دو سلف که خود القایی آنها به ترتیب ۵۵ و ۷۵ میلی‌هانری است به صورت موازی به یکدیگر متصل شده‌اند. اندوکتانس متقابل آنها ۵/۲۲ میلی‌هانری داده شده است. اندوکتانس کل ترکیب موازی را محاسبه کنید.
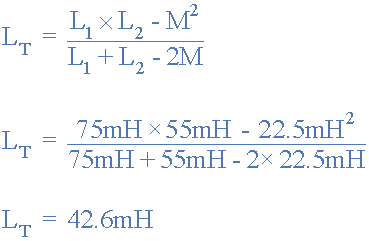
مثال 3) اتصال موازی سلف‌ها
اندوکتانس معادل مدار سلفی زیر را به دست آورید.
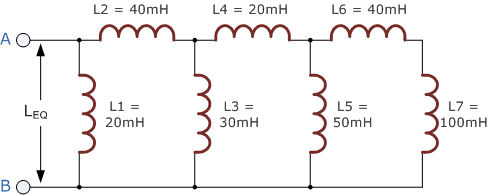
مثال 4) اتصال موازی سلف‌ها
دو سلف L۶ و L۷ که با سلف L۵ موازی هستند را با نام LA به صورت زیر به دست می‌آوریم:
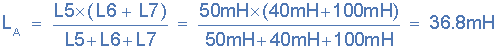
دو سلف L۴ و LA که با سلف L۳ موازی هستند را با نام LB به صورت زیر به دست می‌آوریم:
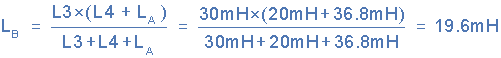
دو سلف L۲ و LB که با سلف L۱ موازی هستند را با نام LEQ به صورت زیر به دست می‌آوریم:
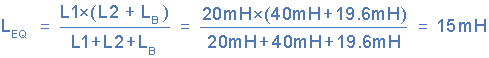
پس اندوکتانس معادل مدار بالا در انتها برابر با ۱۵ میلی‌هانری به دست آمد.
خلاصه اتصال موازی سلف ها
همانند مقاومت، سلف‌هایی که به صورت موازی به هم متصل شده‌اند، ولتاژ یکسانی در دوسرشان دارند. همچنین اتصال موازی سلف‌ها به یکدیگر، اندوکتانس موثر مدار را کاهش میدهد و معکوس اندوکتانس معادل n سلف که به صورت موازی متصل هستند، برابر با مجموع معکوس اندوکتانس‌های تک‌تک سلف‌های مجموعه است. مانند اتصال سری سلف‌ها، سلف‌های موازی دارای اندوکتانس متقابل، بسته به اینکه سیم‌پیچ‌ها به صورت تجمعی (در یک جهت) یا به طور متفاوت (در جهت مخالف) کوپل شوند، به عنوان «کمک کننده» یا «مخالف» این اندوکتانس کل طبقه‌بندی می‌شوند. تا اینجا ما سلف را به عنوان یک المان پسیو خالص یا ایده‌آل بررسی کرده‌ایم.
در مقاله بعدی در مورد سلف‌ها، به سلف‌های غیر ایده‌آلی می‌پردازیم که دارای سیم‌پیچ‌های مقاومتی دنیای واقعی هستند که مدار معادل یک سلف سری با مقاومت را تولید می‌کنند و ثابت زمانی چنین مداری را بررسی می‌کنیم.
دیدگاه خود را بنویسید