اتصال سری سلف ها

سلف‌ها را می‌توان در یک اتصال سری به یکدیگر متصل کرد، زمانی که آنها به صورت زنجیره ای به یکدیگر متصل شده و جریان الکتریکی مشترکی دارند. این اتصالات متقابل سلف‌ها شبکه‌های پیچیده‌تری تولید می‌کنند که اندوکتانس کلی آنها ترکیبی از تک تک سلف‌ها می باشد. با این حال، قوانین خاصی برای اتصال سلف‌ها به صورت سری یا موازی وجود دارد و این قوانین مبتنی بر این واقعیت است که هیچ اندوکتانس متقابل یا کوپلینگ مغناطیسی بین سلف‌های جداگانه وجود ندارد.

سلف‌ها زمانی به صورت سری به هم متصل می‌شوند که در یک خط مستقیم، انتهای یکی به انتهای دیگری به هم متصل شوند. در مقاله مقاومت‌های سری دیدیم که مقادیر مختلف مقاومت‌هایی که به صورت سری به هم متصل شده‌اند فقط با هم جمع می‌شوند و این در مورد اندوکتانس نیز صادق است. سلف‌های سری به سادگی «با هم جمع می‌شوند» زیرا تعداد دور‌های سیم‌پیچ به طور موثر افزایش می‌یابد، کل اندوکتانس مدار LT برابر با مجموع همه اندوکتانس‌های مجزا می‌شود.

1) مدار اتصال سری سلف‌ها

جریان (I) که از سلف اول L۱ می‌گذرد، راهی جز عبور از سلف دوم و سوم و غیره ندارد. پس سلف‌های سری یک جریان مشترک دارند که از آنها عبور می‌کند، به عنوان مثال:

IL1 = IL2 = IL3 = IAB …

در مثال بالا، سلف‌های L۱،  L۲ و L۳ همگی به صورت سری بین نقاط A و B به یکدیگر متصل شده‌اند. مجموع افت ولتاژ مجزا در هر سلف را می‌توان با استفاده از قانون ولتاژ کرشهف (KVL) که در آن، VT = V۱ + V۲ + V۳ پیدا کرد و ما از مقاله‌های قبلی در مورد اندوکتانس می‌دانیم که نیروی محرکه خودالقا‌شده در یک سلف به صورت V = L di/dt داده می‌شود.

بنابراین با در نظر گرفتن مقادیر افت ولتاژ جداگانه در هر سلف در مثال بالا، اندوکتانس کل برای ترکیب سری به صورت زیر به دست می‌آید:

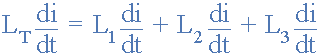
اگر کل مقادیر di/dt را از طرفین معادله بالا حذف کنیم، عبارت نهایی برای اندوکتانس کل مدار در حالتی که سلف‌ها به صورت سری به یکدیگر متصل شده‌اند، به صورت زیر خواهد بود: معادله اتصال سری سلف‌ها

.Ltotal = L۱ + L۲ + L۳ + ….. + Ln etc

 پس اندوکتانس کل زنجیره سری را می‌توان با جمع کردن سلف‌های مجزای سلف‌ها به صورت سری، درست مانند جمع کردن مقاومت‌ها به صورت سری، پیدا کرد. با این حال، معادله فوق تنها زمانی صادق است که «هیچ» اندوکتانس متقابل یا کوپلینگ مغناطیسی بین دو یا چند سلف وجود نداشته باشد (آنها به صورت مغناطیسی از یکدیگر ایزوله شده‌اند). یک نکته مهم در مورد سلف‌ها در مدارهای سری، این است که اندوکتانس کل (LT) هر دو یا چند سلف که به صورت سری به هم متصل شده‌اند، همیشه بزرگتر از مقدار بزرگترین سلف در زنجیره سری خواهد بود.

مثال 1) اتصال سری سلف‌ها
سه سلف با مقادیر ۱۰، ۴۰ و ۵۰ میلی‌هانری در یک ترکیب سری به هم متصل شده‌اند که هیچ اندوکتانس متقابلی بین آنها وجود ندارد. اندوکتانس کل ترکیب سری را محاسبه کنید.

اتصال سری سلف‌ها با حضور اندوکتانس متقابل
هنگامی که سلف‌ها به صورت سری به یکدیگر متصل می‌شوند به طوری که میدان مغناطیسی یکی با دیگری پیوند می‌یابد، اثر اندوکتانس متقابل بسته به میزان کوپلینگ مغناطیسی، اندوکتانس کل را افزایش یا کاهش می‌دهد. اثر این اندوکتانس متقابل به فاصله سیم‌پیچ‌ها و جهت‌گیری آنها نسبت به یکدیگر بستگی دارد. سلف‌های اتصال سری دارای اندوکتانس متقابل، را می‌توان به عنوان «کمک کننده» یا «مخالف» با اندوکتانس کل طبقه‌بندی کرد. اگر شار مغناطیسی تولید شده توسط جریان، از طریق سیم‌پیچ‌ها در یک جهت جریان یابد، سیم‌پیچ‌ها به صورت تجمعی کوپل شده‌اند. اگر جریان از طریق سیم‌پیچ‌ها در جهت مخالف جریان یابد، سیم‌پیچ‌ها مطابق شکل زیر به صورت دیفرانسیلی کوپل شده‌اند.

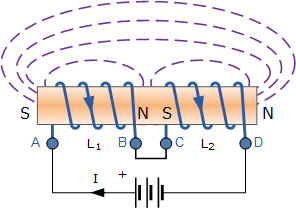3) سلف‌های سری کوپل شده تجمعی

در حالی که جریانی که بین نقاط A و D از طریق دو سیم‌پیچ کوپل‌شده، تجمعی در یک جهت است، معادله بالا برای افت ولتاژ هر یک از سیم‌پیچ‌ها باید اصلاح شود تا برهمکنش بین دو سیم‌پیچ به دلیل اثر اندوکتانس متقابل نیز در این رابطه اعمال شود. خود‌القایی هر سیم‌پیچ جداگانه، L۱ و L۲ مانند قبل خواهد بود اما M که نشان‌دهنده اندوکتانس متقابل است، به آن اضافه می‌شود. پس مجموع نیروی محرکه القا‌شده به سیم‌پیچ‌های کوپل‌شده تجمعی به صورت زیر داده می‌شود:

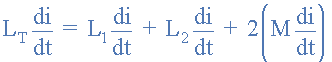
که در فرمول بالا مقدار 2M اثر L۱ بر L۲ به اضافه اثر L۲ بر L۱ می‌باشد. با تقسیم معادله بالا بر di/dt می‌توانیم آن را ساده کنیم تا یک عبارت نهایی برای محاسبه اندوکتانس کل یک مدار در زمانی که سلف‌ها به صورت تجمعی وصل شده‌اند به دست آوریم و این به صورت زیر است:

Ltotal = L ۱ + L ۲ + 2M

اگر یکی از سیم‌پیچ‌ها معکوس شود به طوری که جریان یکسان از هر سیم‌پیچ اما در جهات مخالف عبور کند، اندوکتانس متقابل M که بین دو سیم‌پیچ وجود دارد، مانند شکل زیر روی هر سیم‌پیچ اثر خنثی‌کننده‌ای خواهد داشت.

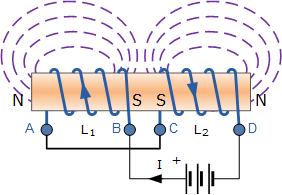۳) سلف های سری کوپل شده دیفرانسیلی

نیروی محرکه که با اثر اندوکتانس متقابل سیم‌پیچ ۲ به سیم‌پیچ ۱ القا می‌شود مخالف با نیروی خود القا‌شده در سیم‌پیچ یک است زیرا اکنون جریان یکسانی از هر سیم‌پیچ در جهات مخالف می‌گذرد. برای در نظر گرفتن این اثر خنثی‌کننده، زمانی که میدان مغناطیسی دو سیم‌پیچ به طور متفاوت به هم متصل می‌شوند، از علامت منفی با M استفاده می‌شود که معادله نهایی را برای محاسبه اندوکتانس کل یک مدار در زمانی که سلف‌ها به طور دیفرانسیلی متصل هستند در اختیار ما قرار می‌دهد:

Ltotal = L ۱ + L ۲ – 2M

پس معادله نهایی برای سلف‌های سری دارای اندوکتانس متقابل به صورت زیر خواهد بود:

مثال 2) اتصال سری سلف‌ها
دو سلف ۱۰میلی‌هانری در یک ترکیب سری به یکدیگر متصل شده‌اند به طوری که میدان‌های مغناطیسی آنها به یکدیگر کمک می‌کنند و کوپل تجمعی ایجاد می‌کنند. اندوکتانس متقابل آنها ۵ میلی‌هانری می‌باشد. اندوکتانس کل ترکیب سری را محاسبه کنید.

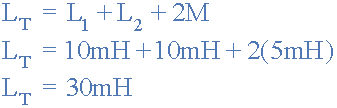
مثال 3) اتصال سری سلف‌ها
دو سیم‌پیچ که به صورت سری به هم متصل شده‌اند، به ترتیب ۲۰ میلی‌هانری و ۶۰ میلی‌هانری خود‌القایی دارند. اندوکتانس کل ترکیب ۱۰۰ میلی‌هانری می‌باشد. مقدار اندوکتانس متقابلی را که بین دو سیم‌پیچ وجود دارد با فرض اینکه آنها به یکدیگر کمک می‌کنند، تعیین کنید.

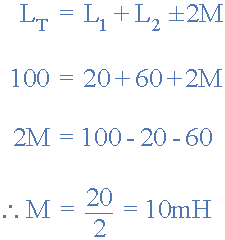
خلاصه اتصال سری سلف‌ها
اکنون می‌دانیم که می‌توانیم سلف‌ها را به صورت سری به یکدیگر متصل کنیم تا یک مقدار اندوکتانس کل LT  برابر با مجموع مقادیر جداگانه تولید کنیم‌، آنها شبیه به اتصال مقاومت‌ها به صورت سری با هم جمع می‌شوند. با این حال، هنگام اتصال سلف‌ها به صورت سری، اندوکتانس متقابل می‌تواند بر آنها تاثیر بگذارد. سلف‌های سری دارای اندوکتانس متقابل، بسته به اینکه سیم‌پیچ‌ها به صورت تجمعی (در یک جهت) یا به‌طور متفاوت (در جهت مخالف) کوپل شده‌اند، به ‌عنوان «کمک‌کننده» یا «مخالف» با اندوکتانس کل طبقه‌بندی می‌شوند.

در مقاله بعدی در مورد سلف‌ها، خواهیم دید که موقعیت سیم‌پیچ‌ها هنگام اتصال سلف‌ها به صورت موازی بر روی اندوکتانس کل LT مدار نیز تاثیر می‌گذارد.