مدار تشدید موازی

تشدید  موازی، زمانی‌ اتفاق می‌افتد؛ که فرکانس منبع تغذیه، اختلاف فاز صفر، بین  ولتاژ تغذیه و جریان داشته باشد و یک مدار مقاومتی ایجاد کند.

از بسیاری جهات، مدار تشدید موازی، همان مدار تشدید سری است؛ که در مقاله قبلی بررسی کردیم. هر دو شبکه سه عنصری، که حاوی دو عنصر  راکتیو می‌باشد؛ به یک مدار مرتبه دوم تبدیل می‌گردد و هردو تحت تاثیر  تغییرات فرکانس منبع تغذیه قرار گرفته و هردو دارای یک نقطه‌ی فرکانسی بوده  که در آن هردو عنصر راکتیو، با خنثی‌کردن یک‌دیگر، بر مشخصات مدار تاثیر  می‌گذارند. هردو مدار دارای یک نقطه فرکانس تشدید می‌باشند.

تفاوت این‌بار این است؛ که مدار توسط جریان‌های جاری در هر شبکه موازی درون مدار مخزن (tank) موازی LC تحت تاثیر قرار می‌گیرد. یک مدار مخزن، ترکیب موازی L و C بوده؛  که در شبکه‌های فیلتری برای انتخاب یا رد فرکانس‌های AC استفاده می‌گردد.  مدار موازی RLC زیر را در نظر بگیرید.

مدار موازی RLC

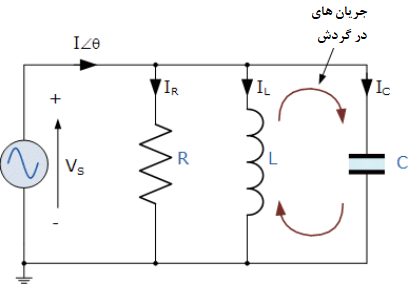1. مدار  RLC موازی

ابتدا، اجازه دهید، آنچه را که تا الان در مورد مدارهای موازی RLC، می‌دانیم با هم مرور کنیم :

                    ادمیتانس

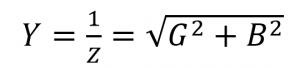
هدایت

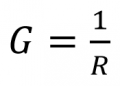
سوسپتانس القایی

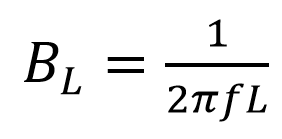
سوسپتانس خازنی

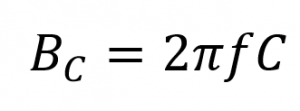
یک مدارموازی حاوی مقاومت R ، اندوکتانس L  و ظرفیت خازنی C  است؛ که یک مدار تشدید موازی؛  هنگامی‌که جریان حاصل از ترکیب موازی، هم‌فاز با ولتاژ منبع تغذیه باشد؛  تولید می‌کند(هم‌چنین به‌عنوان ضد تشدید نیز خوانده می‌شود). در تشدید، یک  گردش بزرگ از جریان، بین سلف و خازن، به‌دلیل انرژی نوسانات، وجود دارد؛ که  سبب می‌شود مدار موازی، جریان تشدید تولید نماید.

یک مدار تشدید موازی،  انرژی مدار را، در میدان‌الکتریکی سلف و میدان‌الکتریکی خازن ذخیره  می‌کند. این انرژی دائما بین سلف و خازن مبادله می‌شود؛ که نتیجه‌ی آن  جریان و انرژی صفر منبع است. دلیل این امر آن است؛ که مقادیر لحظه‌ای IL و IC همیشه برابر و در خلاف جهت‌هم بوده و بنابراین، جریانی که از منبع تغذیه  گرفته می‌شود؛ جمع برداری دو جریان و نیز جریان جاری در مقاومت R ( IR) است.

درحل  مدارهای تشدید موازی AC، می‌دانیم که ولتاژ منبع تغذیه، برای همه شاخه‌ها  مشترک می‌باشد؛ درنتیجه، می‌توانیم آن را عنوان بردار مرجع درنظر بگیریم.  با هر شاخه موازی، باید جداگانه مانند مدارهای سری رفتار شود؛ به‌طوری‌که،  کل‌جریان منبع تغذیه ای که توسط مدار موازی گرفته می‌شود؛ جمع برداری  جریان‌های شاخه‌های منفرد باشد.

پس دو روش در تجزیه‌و‌تحلیل مدارهای  تشدید موازی، در دسترس ما می‌باشد. ما‌ می‌توانیم جریان را در هرشاخه  محاسبه کنیم، سپس باهم جمع نماییم یا ادمیتانس هر شاخه را برای یافتن جریان  کل به‌دست آوریم. ازمقاله قبلی در مورد تشدید سری می‌دانیم؛ که تشدید،  زمانی رخ می‌دهد؛ که VL= -VC باشد و این وضعیت، زمانی اتفاق می‌افتد که دو راکتانس با هم برابر باشند(XL=XC ). ادمیتانس مدار موازی به صورت زیر خواهد بود:

تشدید، زمانی رخ می‌دهد که XL=XC باشد و بخش موهومی Y، صفر شود. پس:

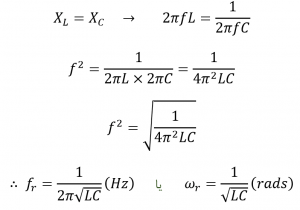
توجه داشته باشید؛ که در تشدید، یک مدار موازی همان معادله‌ای را  تولید می‌کند؛ که در مدار تشدید سری تولید می‌شود. از این‌رو، هیچ تفاوتی  بین این‌که، سلف یا خازن،  موازی یا سری متصل شده باشد؛ نیست. هم‌چنین در تشدید، یک مدار مخزن موازی  LC مانند یک مدارباز عمل می‌کند و جریان مدار، فقط توسط مقاومت R تعیین  می‌شود. بنابراین امپدانس کل مدار تشدید موازی هنگام تشدید، فقط به مقدار  مقاومت مدار بستگی دارد و Z=R خواهد بود. همانطور که زیر نشان داده  شده‌است.

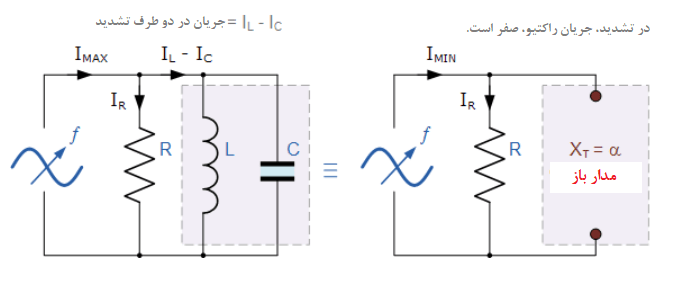۲. امپدانس مدار تشدید موازی

بنابراین، در تشدید، امپدانس مدار موازی در حداکثر مقدار خود بوده و برابر با مقاومت مدار است؛ که سبب  شرایط مقاومت بالا و جریان کم برای مدار می‌گردد. هم‌چنین در تشدید، از  آن‌جایی که امپدانس مدار تنها برابر با مقاومت است؛ جریان کلی مدار I،  “هم‌فاز” با ولتاژ منبع تغذیه VS است.

می‌توانیم با تغییر  مقدار مقاومت، پاسخ فرکانسی مدار را تغییر دهیم. اگر L و C، ثابت بمانند؛  تغییر مقدار R، بر اندازه‌ی جریان جاری در مدار هنگام تشدید، اثر دارد. پس  امپدانس مدار در تشدید Z=RMAX بوده که امپدانس “دینامیک مدار” خوانده می‌شود.

امپدانس در مدار تشدید موازی

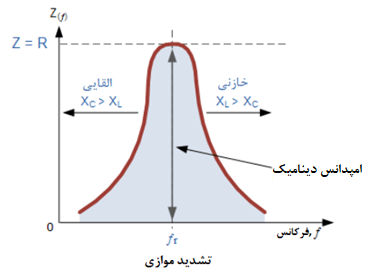
توجه داشته باشید؛ که اگر امپدانس مدارهای موازی درتشدید، در حداکثر مقدار خود باشد، درنتیجه، ادمیتانس مدار باید حداقل باشد و یکی از مشخصات مدار تشدید موازی؛ ادمیتانس بسیار  کم است که جریان مدارها را محدود می‌کند. برخلاف مدار تشدید سری، مقاومت در  مدار تشدید موازی، دارای اثرمیرایی بر روی پهنای‌باند است و باعث می‌شود؛  مدار کمتر، انتخاب‌پذیر باشد.

هم‌چنین، به‌دلیل ثابت بودن جریان  مدار، برای هرمقداری از امپدانس Z، ولتاژ دوسر مدار تشدید موازی، برابر با  همان شکل امپدانس کل خواهد بود و برای یک مدار موازی، شکل‌موج ولتاژ به‌طور  کلی از دوسر خازن گرفته می‌شود.

می‌دانیم که در فرکانس تشدید (fr)،  ادمیتانس مدار، حداقل بوده و برابر با هدایت (G) بوده که با 1/R بیان  می‌شود. زیرا در یک مدار تشدید موازی، قسمت موهومی ادمیتانس، یعنی سوسپتانس  B برابر با صفر بوده زیرا BL=BC است. همانطور که زیر نشان داده شده است.

سوسپتانس در تشدید

۳. سوسپتانس در تشدید

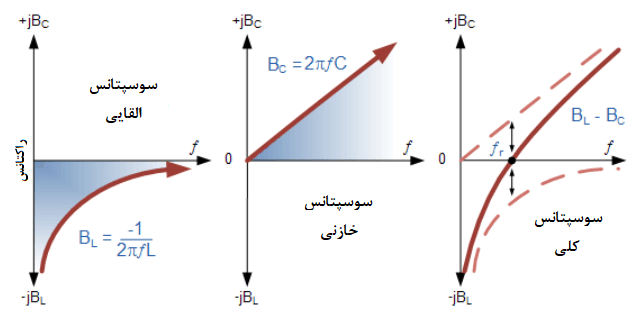
از بالا، سوسپتانس القایی BL، با فرکانس به‌صورت معکوس متناسب است؛ که با منحنی هایپربولیک نشان داده می‌شود. سوسپتانس خازنی BC،  با فرکانس به‌صورت مستقیم متناسب است؛ که با یک خط مستقیم نمایش داده  می‌شود. منحنی نهایی نمودار، نشان‌دهنده‌ی رسم سوسپتانس کلی مدار تشدید  موازی، در برابر تغییر فرکانس و نیز تفاوت دو مقدار سوسپتانس است.

و  نیز می‌توانیم ببینیم که در نقطه‌ی فرکانس تشدید، اگر از محور افقی عبور  کند؛ سوسپتانس کلی مدار برابر با صفر است. زیر نقطه فرکانس تشدید، سوسپتانس  القایی بر مدار غلبه کرده و سبب ایجاد ضریب توان “لگ” می‌شود؛ در حالی‌که  بالای نقطه‌ی فرکانس تشدید، سوسپتانس خازنی غلبه نموده که ضریب توان “لید”  ایجاد می‌کند.

بنابراین، در فرکانس تشدید، جریان دریافتی از منبع  باید با ولتاژ اعمال‌شده هم‌فاز باشد؛ زیرا در مدار موازی فقط مقاومت وجود  دارد؛ بنابراین ضریب توان 1 یا واحد است (θ=0°). هم‌چنین، به دلیل تغییر  امپدانس مدار موازی با فرکانس، امپدانس مدار، “دینامیک” خواهد بود؛ و  جریانی که در تشدید هم‌فاز با ولتاژ است، سبب می‌شود، امپدانس مدار مانند  مقاومت عمل می‌کند. و نیز دیدیم که امپدانس مدار موازی در تشدید، معادل  مقدار مقاومت بوده و بنابراین این مقدار باید حداکثر امپدانس دینامیکی (Zd) مدار را نشان دهد؛ که در زیر نشان داده شده است.

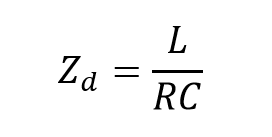
جریان در مدار تشدید موازی

از آن‌جایی که، سوسپتانس کل در فرکانس تشدید، برابر با صفر است؛  ادمیتانس، حداقل بوده و برابر با مقدار هدایت G می‌باشد. از این‌رو، در  تشدید، جریان جاری در مدار باید حداقل باشد؛ از آن‌جایی که جریان‌های شاخه  القایی و خازنی برابر با یکدیگر بوده ( IC=IL ) و  °180 خارج فاز است. به‌یاد می‌آوریم؛ که جریان کل جاری در مدار موازی RLC،  برابر با مجموع برداری جریان‌های شاخه‌های منفرد بوده و به‌صورت زیر، برای  فرکانس تعیین‌شده محاسبه می‌گردد:

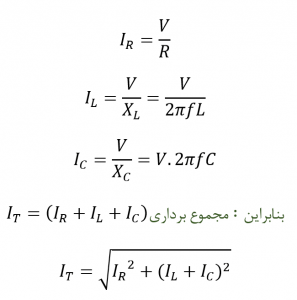
در تشدید، جریان‌های IL و IC برابر بوده و شبکه راکتیو را خثنی کرده که برابر با صفر می‌گردد. پس در تشدید، معادله بالا به‌صورت زیر در می‌آید:

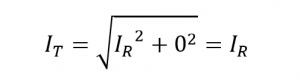
به‌دلیل این‌که، جریان جاری در یک مدار تشدید موازی، از تقسیم  ولتاژ بر امپدانس حاصل می‌گردد. در تشدید، امپدانس Z، حداکثر مقدار خود (=R  ) می‌باشد. از این‌رو، جریان مدار در این فرکانس، برابر با حداقل مقدار  V/R مدار بوده و نمودار جریان در برابر تغییر فرکانس برای یک مدار تشدید  موازی به صورت زیر است:

جریان مدار موازی در تشدید

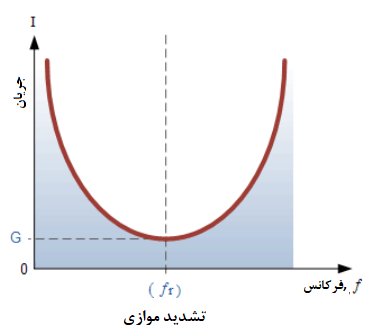۴. جریان مدار تشدید موازی

منحنی پاسخ فرکانسی یک مدار تشدید موازی، نشان می‌دهد؛ که مقدار  جریان، تابعی از فرکانس است و رسم آن بر روی نمودار به ما نشان می‌دهد؛ که  پاسخ در مقدار حداکثر خود آغاز می‌گردد، به مقدار حداقل خود در فرکانس  تشدید، زمانی‌که IMIN=IR بوده؛ می‌رسد و سپس دوباره با بی‌نهایت شدن f، افزایش می‌یابد.

نتیجه  این خواهد بود؛ که مقدار جریان جاری در سلف L و خازن C مدار مخزن،  می‌تواند، حتی در تشدید، بسیار بزرگتر از جریان منبع‌تغذیه گردد؛ اما  به‌دلیل برابر و در جهت مخالف یک‌دیگر بودن (180°خارج فاز) یک‌دیگر را به  صورت موثری، خنثی می‌کنند.

از آن‌جایی که، مدار تشدید موازی، تنها بر روی فرکانس تشدید کار می‌کند؛ این نوع مدار، به‌عنوان مدار ردکننده نیز شناخته می‌شود. زیرا در تشدید، امپدانس مدار در بیشترین حد خود است.  بنابراین، جریانی را که فرکانس آن، برابر با فرکانس تشدید آن است، به‌شدت  سرکوب یا رد می‌کند. اثر تشدید در مدار موازی، “تشدید جریان” نیز خوانده  می‌شود.

محاسبات و نمودارهای استفاده‌شده در بالا، برای تعریف مدار  تشدید موازی، مشابه آن چیزی است که برای مدار سری استفاده کردیم. با  این‌حال، مشخصات و نمودارهای ترسیم‌شده برای یک مدار موازی؛ دقیقا مخالف  مدارهای سری، با حداکثر و حداقل امپدانس، جریان و بزرگنمایی معکوس است.  به‌همین دلیل می‌باشد؛ که به مدار تشدید موازی، مدار ضد تشدید، نیز می‌گویند.

پهنای باند و انتخاب مدار تشدید موازی

پهنای‌باند یک مدار تشدید موازی، دقیقا به روشی مشابه به مدار تشدید سری؛ تعریف می‌گردد. فرکانس‌های قطع بالا و پایین به‌صورت:  fupper و flower ارائه می‌شوند که به ترتیب؛ فرکانس‌های نصف توانی را نشان می‌دهد؛ که در  آن، توان اتلاف‌شده در مدار، نیمی از توان‌کل تلف‌شده در فرکانس تشدید است  (0.5(I۲R)) که به ما همان نقاط3db – را می‌دهد؛ که در آن، مقدار جریان برابر با 70.7% مقدار حداکثر تشدید خود است ((0.707*I)۲R).

همانند  مدار سری، اگر فرکانس تشدید ثابت بماند؛ افزایش ضریب کیفیت Q، سبب کاهش  پهنای‌باند شده و به‌همین ترتیب، کاهش ضریب کیفیت، سبب افزایش پهنای‌باند  خواهد بود که خواهیم داشت:

هم‌چنین، با تغییر نسبت بین سلف L و خازن C یا مقدار مقاومت R،  پهنای‌باند و به دنبال‌آن، پاسخ فرکانسی مدار، برای یک فرکانس تشدید ثابت،  تغییر می‌کند. این روش به صورت گسترده، در تنظیم مدارهای فرستنده و گیرنده  رادیویی و تلویزیونی استفاده می‌شود.

انتخاب‌پذیری یا ضریب Q برای یک  مدار تشدید موازی، به‌طور کلی، به‌عنوان نسبت جریان‌های جاری در شاخه به  جریان تغذیه، تعریف شده و به صورت زیر ارائه می‌گردد:

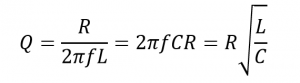
توجه داشته باشید؛ که ضریب Q یک مدار تشدید موازی، بیان معکوس  ضریب  Q برای یک مدار تشدید سری است. هم‌چنین در مدارهای تشدید سری، ضریب  Q، بزرگ‌نمایی ولتاژ مدار را ارائه می‌دهد؛ درحالی‌که، برای یک مدار موازی،  بزرگ‌نمایی جریان را نشان می‌دهد.

پهنای باند مدار تشدید موازی

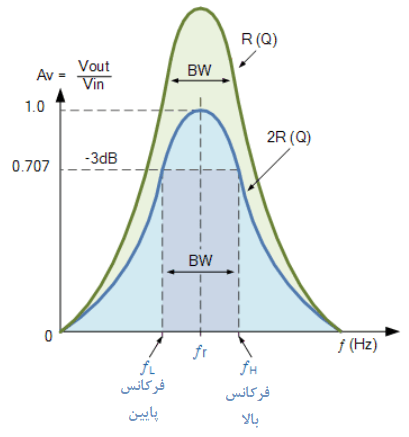۵. پهنای باند مدار تشدید موازی

مثال شماره ۱ -  تشدید موازی

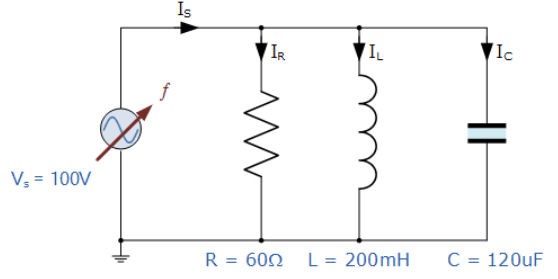
یک شبکه‌ی تشدید موازی، متشکل از یک مقاومت 60Ω، یک خازن 120uF و  یک سلف 200mH به یک ولتاژ منبع تغذیه سینوسی متصل است؛ که دارای خروجی  ثابت 100 ولت برای همه فرکانس‌هاست. فرکانس تشدید، ضریب کیفیت، پهنای‌باند  مدار، جریان در هنگام تشدید و بزرگ‌نمایی جریان را محاسبه کنید.

فرکانس تشدید ƒr

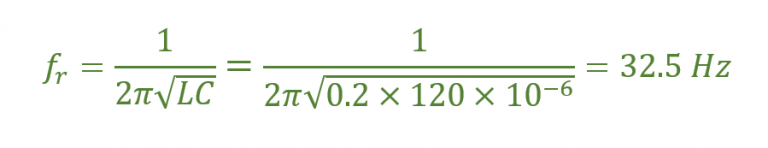
راکتانس القایی هنگام تشدید XL

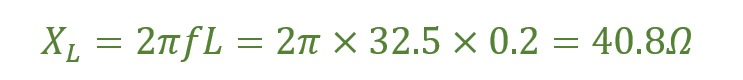
ضریب کیفیت Q

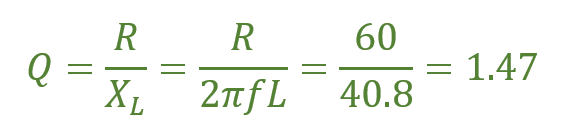
پهنای باند BW

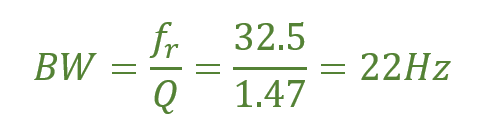
نقاط فرکانس پایین و بالای 3dB-

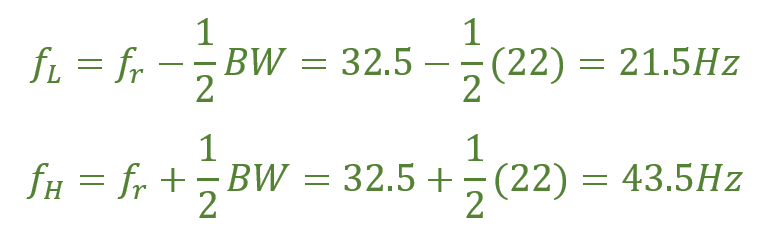
جریان مدار هنگام تشدید IT

در تشدید، امپدانس دینامیک مدار برابر با R است.

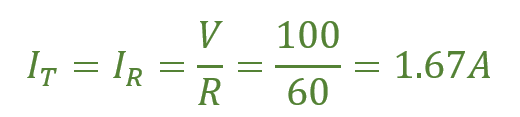
بزرگ نمایی جریان Imag

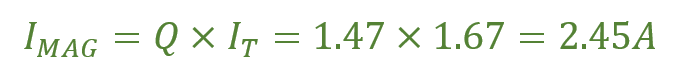
باید توجه داشت؛ که جریان دریافت‌شده از منبع در تشدید (جریان  مقاومتی)، تنها برابر با 1.67 آمپر است؛ در حالی‌که، جریان جاری در مدار  مخزن LC بزرگتر از 2.45 آمپر خواهد بود. ما می‌توانیم، این مقدار را با  محاسبه جریان عبوری از طریق سلف ( یا خازن ) در تشدید بررسی کنیم.

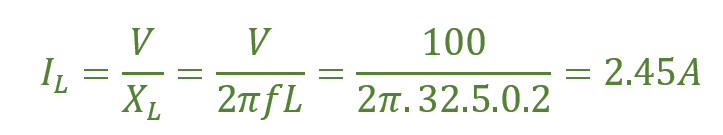
خلاصه آموزش تشدید موازی

دیدیم؛ که مدارهای تشدید موازی، شبیه مدارهای تشدید سری می‌باشند.

تشدید  در مدارهای موازی RLC، زمانی رخ می‌دهد؛ که جریان کلی مدار، “هم‌فاز” با  ولتاژ منبع تغذیه باشد؛ هنگامی‌که دو عنصر راکتیو، یک‌دیگر را خنثی  می‌کنند.

در تشدید، ادمیتانس مدار، حداقل بوده و برابر با هدایت مدار  است. هم‌چنین در تشدید، جریان دریافتی از منبع نیز، حداقل است و با مقدار  مقاومت موازی تعیین می‌شود.

معادله‌ای که برای محاسبه‌ی نقطه‌ی  فرکانس تشدید استفاده می‌شود؛ همانند مدار سری است. با این‌حال، استفاده از  اجزای خالص یا ناخالص در مدار RLC سری برای محاسبه فرکانس تشدید تاثیرگذار  نیست؛ اما در یک مدار موازی RLC، تاثیرگذار می‌باشد.

در این آموزش  درمورد تشدید موازی، فرض کردیم که دو عنصر راکتیو، القایی خالص و خازنی  خالص با مقاومت صفر می‌باشند. با این‌حال، در واقعیت، سلف دارای مقداری  مقاومت سری RS با سیم‌پیچ القایی خود خواهد بود؛ زیرا سلف‌ها (و  سلونوئیدها) کویل‌های از سیم می‌باشند که معمولا از مس که دور یک هسته  مرکزی پیچیده شده است؛ ساخته می‌شود.

بنابراین، معادله‌ی اساسی فوق، برای محاسبه‌ی فرکانس تشدید موازی fr یک مدار تشدید موازی خالص، باید کمی اصلاح گردد تا از سلف ناخالصی که دارای یک مقاومت سری است؛ استفاده شود.

فرکانس تشدید هنگام استفاده سلف ناخالص

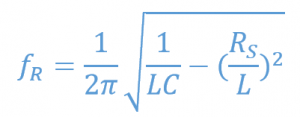
درجایی‌که، L اندوکتانس یک کویل، C خازن موازی و RS مقدار مقاومت DC یک کویل است.