مدار RLC موازی

مدار RLC موازی ، نقطه مقابل مدار سری است؛ که در مقاله قبل بررسی کردیم.گرچه برخی از مفاهیم و معادلات قبلی ، هنوز هم کاربرد دارند.

به‌هر‌حال، تجزیه‌و‌تحلیل مدار موازی RLC،  می‌تواند از نظر ریاضیاتی، دشوارتر از مدار سری RLC باشد؛ بنابراین در این  آموزش در مورد مدار های موازی RLC، تنها المان‌های خالص برای مدار در نظر  گرفته می‌شود تا در این آموزش، کارها ساده باشد.

این‌بار، به‌جای  آن‌که، جریان در اجزای مدار مشترک باشد؛ ولتاژ اعمال‌شده برای همه آن‌ها  مشترک است. بنابراین ما باید جریان انشعابات جداگانه را از طریق هر المان  بیابیم. امپدانس کلی مدار (Z) برای یک مدار موازی RLC، با استفاده از جریان مدار، مشابه  مدار موازی DC، محاسبه می‌گردد. تفاوت موجود تنها این است؛ که به‌جای  امپدانس، از ادمیتانس استفاده می‌شود. مدار موازی RLC زیر را در نظر  بگیرید.

مدار موازی RLC

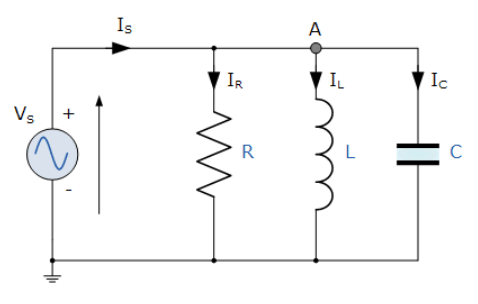
1. مدار موازی RLC

در مدار موازی RLC بالا، می‌بینیم که ولتاژ تغذیه (VS) برای همه این سه المان مشترک است؛ در‌حالی‌که جریان تغذیه (IS) از سه بخش تشکیل می‌شود؛ جریان جاری در مقاومت را IR ، جریان جاری در سلف را IL و جریان جاری در خازن را IC می‌نامیم.

 اما جریان جاری در هر انشعاب و از این‌رو، در هر عنصر، با یک‌دیگر و نیز با جریان منبع تغذیه IS متفاوت می‌باشد. جریان کلی جاری‌شده از منبع تغذیه، جمع ریاضیاتی هر انشعاب منفرد نبوده، بلکه مجموع برداری آن‌ها خواهد بود.

همانند مدار سری RLC، می‌توانیم این مدار را، با روش فازور یا برداری حل کنیم؛ اما این‌بار، نمودار برداری، ولتاژ را به عنوان مرجع  خود گرفته و سه بردار دیگر جریان، با توجه به آن رسم خواهند شد. نمودار  فازوری برای مدار موازی RLC، با ترکیب کردن هر فازور منفرد برای هر عنصر و  اضافه‌کردن جریان‌ها به صورت بردار تولید می‌شود.

به دلیل این‌که، ولتاژ در مدار در هر سه عنصر مدار مشترک است؛ می‌توان آن را به عنوان بردار مرجع برای رسم سه ولتاژ با زاویه‌های مربوطه، در نظر گرفت. بردار حاصل (IS) را می‌توان با اضافه‌نمودن دو بردار  IL و  IC به یک‌دیگر و پس از آن، اضافه نمودن حاصل به‌دست آمده به بردار باقی‌مانده IR به دست‌آورد. زاویه حاصل بین V و IS، زاویه فاز مدار خواهد بود که در زیر آورده شده‌است.

نمودار فازور برای مدار موازی RLC

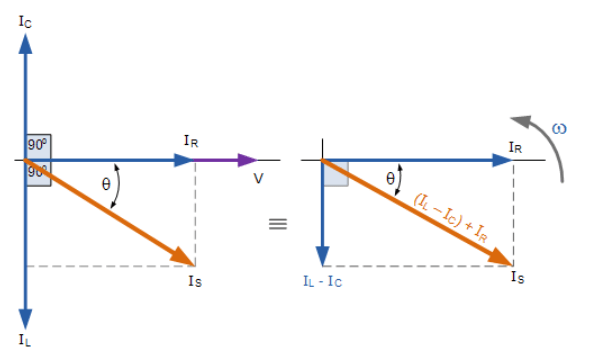
2. نمودار فازور برای مدار موازی RLC

از نمودار فازوری در سمت راست تصویر بالا، می‌توانیم ببینیم که بردارهای جریان یک مثلث مستطیل شکل را تشکیل می‌دهند، که از وتر IS، محور افقی IR و محور عمودی IL-IC تشکیل شده‌است که سبب ساخته‌شدن مثلث جریان می‌گردد و از قضیه فیثاغورث می‌توان در این مثلث جریان استفاده نمود تا از  نظر ریاضیاتی اندازه‌های منفرد هر انشعاب را در امتداد محور x و محورy   به‌دست آوریم؛ که مقدار IS این عناصر را همانطور که نشان داده‌شده، تعیین کنیم.

مثلث جریان برای مدار  RLC موازی

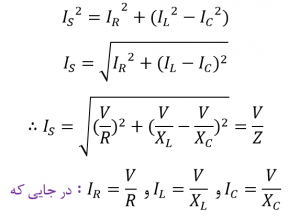
به دلیل مشترک‌بودن ولتاژ مدار برای هر سه المان مدار، جریان هر  انشعاب را می‌توان با استفاده از قانون جریان کیرشهف (KCL) به‌دست آورد. به  یاد داشته‌باشید؛ که قانون جریان کیرشهف یا قانون اتصال می‌گوید که “کل  جریانی که به یک گره یا اتصال وارد می‌شود، دقیقا برابر با جریان خارج شده  از آن است.” بنابراین، جریان‌های ورودی و خروجی به گره “A“ در بالا خواهد بود:

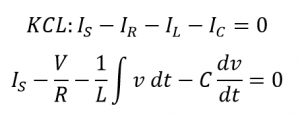
با استفاده از مشتق و تقسیم معادله‌ی فوق بر C و سپس تنظیم مجدد  آن، به ما معادله مرتبه دوم زیر را برای جریان مدار می‌دهد. این معادله به  این دلیل که، دارای دو عنصر راکتیو سلف و خازن است؛ مرتبه دوم است.

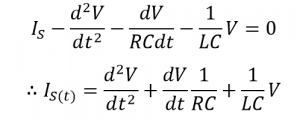
میزان مخالفت با جریان جاری در این نوع مدار AC دارای سه مولفه‌ی XL ، XC و R است؛ که با ترکیب نمودن مقادیر آن‌ها امپدانس (Z) مدار تعیین می‌شود.  از بالا می‌دانیم که ولتاژ، دامنه و فاز یکسانی در تمام عناصر مدار موازی  RLC دارد؛ در نتیجه امپدانس هر عنصر را از نظر ریاضیاتی می‌توان نسبت به  جریان جاری در آن یافت. ولتاژ دوسر هر عنصر خواهد بود:

امپدانس مدار موازی RLC

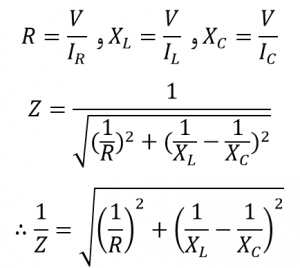
از آخرین معادله برای مدار موازی RLC، می‌توان متوجه شد که برای  هر شاخه‌ی موازی یک امپدانس مختلط تولید می‌گردد؛ از آنجایی که هر عنصر به  معکوس امپدانس تبدیل می‌گردد، به معکوس امپدانس معمولا ادمیتانس گفته می‌شود که نماد آن Y است.

در  مدارهای موازی AC، معمولا استفاده از ادمیتانس برای حل امپدانس مختلط  شاخه، مخصوصا در زمانی‌که، دو با چند شاخه موازی درگیر باشند راحت‌تر است  (به ریاضیات کمک می‌کند). ادمیتانس کلی مدار را می‌توان با اضافه‌کردن  ادمیتانس‌های موازی یافت؛ بنابراین امپدانس کلی مدار (ZT) برابر با (1/YT) برحسب زیمنس خواهد بود.

ادمیتانس یک مدار  RLC موازی

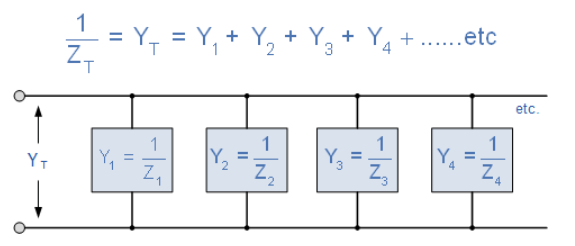3.  ادمیتانس مدار  RLC موازی

واحد سنجشی که امروزه، معمولا برای ادمیتانس استفاده می‌شود؛ زیمنس است که به اختصار با S گفته می‌شود (واحد قدیمی موهو (Ʊ) بوده که عکس اهم  (Ω) است.) ادمیتانس‌ها با یک‌دیگر در شاخه‌های موازی جمع می‌شوند؛  درحالی‌که، امپدانس‌ها در شاخه‌های سری با هم جمع می‌شوند. اما اگر بتوانیم  معکوس امپدانس را داشته باشیم؛ می‌توانیم معکوسی مقاومت و راکتانس را نیز  داشته‌باشیم. از آن‌جایی‌که امپدانس دارای دو مولفه R و X است؛ درنتیجه  معکوس مقاومت، هدایت (رسانایی) و معکوس راکتانس، سوسپتانس نامیده می‌شود.

رسانایی، ادمیتانس و سوسپتانس

واحدهایی که برای هدایت، ادمیتانس و سوسپتانس استفاده می‌شوند؛  همگی یکسان بوده و برحسب زیمنس (S) می‌باشند که می‌توان آن‌ها را معکوس اهم  (ohm-۱) نیز دانست. اما نماد مورداستفاده برای هر عنصر متفاوت بوده و برای یک عنصر خالص داریم:

ادمیتانس (Y)

ادمیتانس، معکوس امپدانس (Z) بوده و دارای نماد Y است. در  مدارهای AC، ادمیتانس به سهولتی گفته می‌شود؛ که در آن، یک مدار تشکیل‌شده  از مقاومت‌ها و راکتانس‌ها، هنگام اعمال ولتاژ با در نظرگرفتن اختلاف فاز  میان ولتاژ و جریان، به جریان اجازه جاری شدن می‌دهد.

ادمیتانس یک مدار موازی، نسبت فازور جریان به فازور ولتاژ بوده با زاویه‌ای که ادمیتانس نسبت به امپدانس با مقدار منفی دارد.

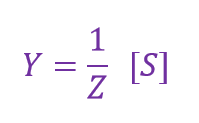
سوسپتانس (B)

سوسپتانس، معکوس راکتانس خالص (X) بوده و دارای نماد B است. در مدارهای AC، سوسپتانس به سهولتی  گفته می‌شود؛ که در آن راکتانس ( یا دسته‌ای از راکتانس‌ها)، هنگام که  ولتاژ با یک فرکانس مشخص اعمال می‌شود؛ به جریان متناوب اجازه جاری‌شدن  می‌دهد.

سوسپتانس، دارای علامتی معکوس راکتانس است؛ از این‌رو، مقدار سوسپتانس خازنی (BC) مثبت بوده (Ve+)؛ در حالی‌که سوسپتانس القایی (BL) دارای مقدار منفی (Ve-) است.

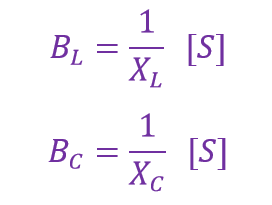
می‌توانیم سوسپتانس القایی و خازنی را به صورت زیر تعریف کنیم:

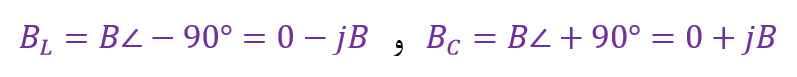
در مدارهای سری AC، میزان مخالفت با جریان جاری امپدانس (Z) بوده  که دارای دو مولفه‌ی مقاومت (R) و راکتانس (X) است و از این دو مولفه  می‌توان مثلث امپدانس را ساخت. به طور مشابه، در مدارهای موازی RLC،  ادمیتانس (Y) دارای دو مولفه‌ی هدایت (G) و سوسپتانس (B) می‌باشد و ساختن  مثلث ادمیتانس را ممکن می‌سازد که دارای محور افقی رسانایی (G) و دارای  محور عمودی سوسپتانس (jB) به صورت زیر می‌باشد.

مثلث ادمیتانس برای مدار RLC موازی

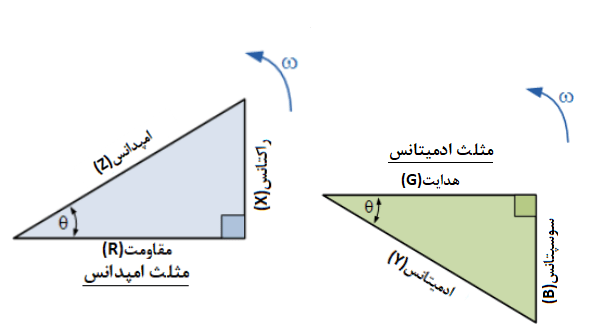4. مثلث ادمیتانس برای مدار RLC موازی

اکنون که مثلث ادمیتانس را داریم؛ می‌توانیم از فیثاغورث برای  محاسبه‌ی اندازه هر سه ضلع و هم‌چنین زاویه‌فاز، همان‌طور که نشان داده  شده‌است؛ استفاده کنیم.

از فیثاغورث:

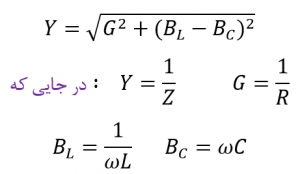
سپس می‌توانیم ادمیتانس مدار و امپدانس را در رابطه با ادمیتانس تعریف کنیم:

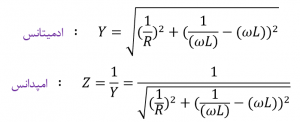
ضریب توان زاویه:

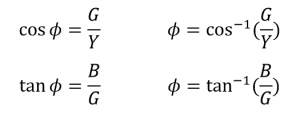
همان‌طور که ادمیتانس یک مدار موازی RLC، یک مقدار مختلط است؛  اگر بخواهیم ادمیتانس را به فرم عمومی امپدانس Z=R+jX که در مدارهای سری  برقرار است بنویسیم؛ می‌توان برای مدارهای موازی نوشت: Y=G-jB. در جایی‌که،  بخش حقیقی G ، هدایت و بخش موهومی jB سوسپتانس است. فرم قطبی به ما خواهد  داد:

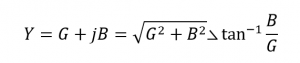
مثال شماره 1 - مدار موازی RLC

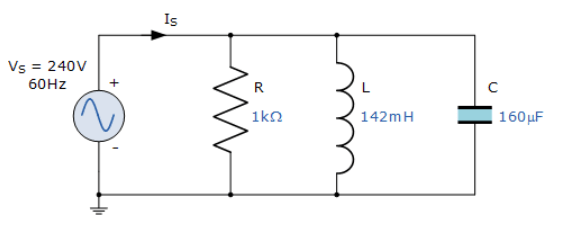
یک مقاومت 1kΩ ، یک کویل 142mH و یک خازن 160uF ، همه به صورت  موازی به یک منبع تغذیه 240V و 60Hz متصل شده‌اند. امپدانس مدار موازی RLC و  جریان دریافتی از منبع را محاسبه کنید.

امپدانس مدار موازی RLC

در یک مدار AC، مقاومت تحت‌تاثیر فرکانس قرار نمی‌گیرد. بنابراین R=1kΩ

راکتانس القایی (XL)

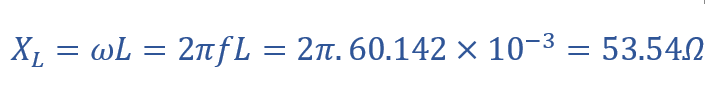
راکتانس خازنی (XC)

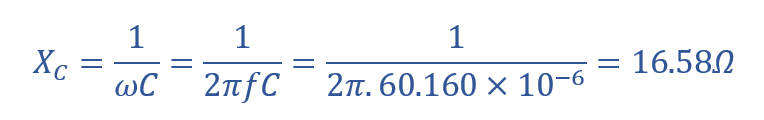
5. امپدانس مدار موازی RLC - مثال 1

امپدانس (Z)

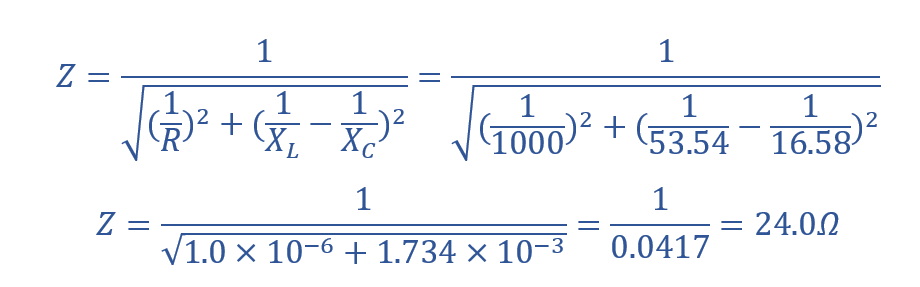
جریان منبع تغذیه (IS)

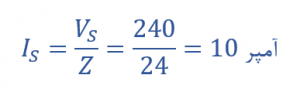
مثال شماره 2 - مدار موازی RLC

یک مقاومت 50Ω ، یک کویل 20mH و یک خازن 5uF ، همه به صورت موازی  به یک منبع تغذیه 50V و 100Hz متصل شده‌اند. جریان کل حاصل از منبع‌تغذیه،  امپدانس کل مدار و زاویه فاز را محاسبه کنید. هم‌چنین مثلث جریان و  ادمیتانس مدار را نیز رسم کنید.

مدار موازی RLC

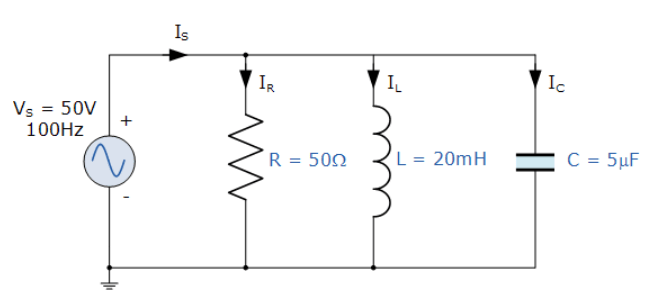6. مدار موازی RLC - مثال2

 راکتانس القایی (XL)

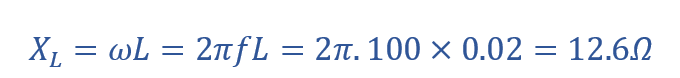
راکتانس خازنی (XC)

امپدانس (Z)

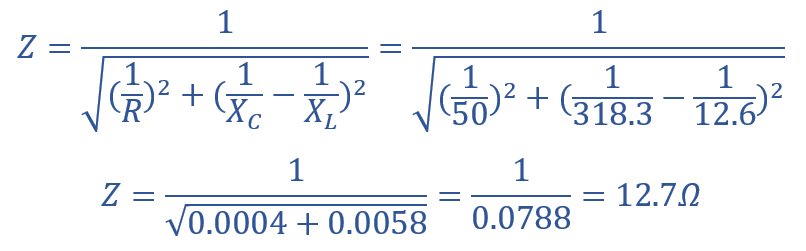
جریان عبوری از مقاومت R (IR)

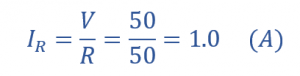
جریان عبوری از سلف L (IL)

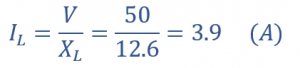
جریان عبوری از خازن C (IC)

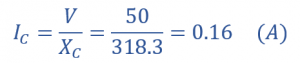
جریان کلی منبع تغذیه (IS)

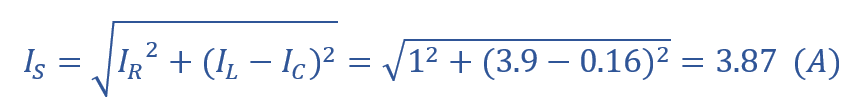
هدایت (G)

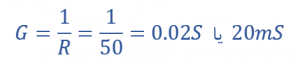
سوسپتانس القایی (BL)

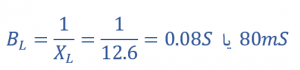
سوسپتانس خازنی (BC)

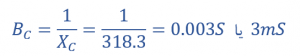
ادمیتانس (Y)

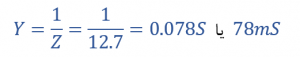
زاویه‌فاز (φ) بین جریان حاصل و ولتاژ منبع تغذیه

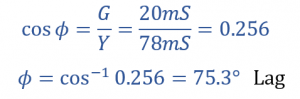
مثلث‌های جریان و ادمیتانس

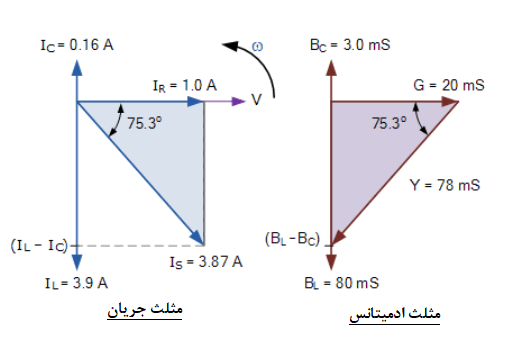۷. مثلث‌ جریان و ادمیتانس

خلاصه مدار موازی RLC

در یک مدار RLC موازی ، که متشکل از مقاومت، سلف و خازن است، جریان مدار (IS)، جمع فازوری تشکیل‌شده از سه مولفه‌ی IR ، ILو IC با ولتاژ منبع‌تغذیه‌ای ‌است که بین این سه مشترک است. از آنجایی‌که ولتاژ  بین تمام سه عنصر مدار مشترک است؛ به عنوان مرجع افقی، زمانی‌که مثلث  جریان را می‌سازیم؛ استفاده می‌گردد.

شبکه‌های موازی RLC را می‌توان،  با استفاده از نمودارهای برداری، همانند مداری سری RLC مورد تجزیه‌و‌تحلیل  قرارداد. با این حال، تجزیه‌‌و‌تحلیل مدارهای موازی RLC، از نظر ریاضیاتی  کمی دشوارتر از مدارهای سری RLC است که دارای دو یا چند شاخه جریان  می‌باشد. بنابراین یک مدار موازی AC، می‌تواند با استفاده از معکوس امپدانس  به نام ادمیتانس به آسانی، تجزیه‌و‌تحلیل شود.

ادمیتانس،  معکوس امپدانس است که دارای نماد Y می‌باشد. همانند امپدانس، یک مقدار  مختلط است؛ که از یک قسمت حقیقی و یک قسمت موهومی تشکیل می‌شود. قسمت  حقیقی، معکوس مقاومت بوده، که رسانایی خوانده می‌شود و دارای نماد G است؛  درحالی‌که، قسمت موهومی، معکوس راکتانس بوده و سوسپتانس نام دارد و نماد آن B است. ادمیتانس در فرم مختلط به صورت: Y=G+jB می‌باشد.

هم‌زادی بین دو امپدانس مختلط را می‌توان به صورت زیر تعریف کرد.

از آن‌جایی‌که، سوسپتانس، معکوس راکتانس است؛ در یک مدار القایی، سوسپتانس القایی (BL) از نظر مقدار منفی خواهد بود و در یک مدار خازنی، سوسپتانس خازنی (BC) از نظر مقدار مثبت بوده که دقیقا برعکس XL و XC می‌باشد.

تاکنون  دیده‌ایم، مدارهای سری و موازی RLC، دارای راکتانس القایی و راکتانس خازنی  در یک مدار می‌باشند. اگر فرکانس را در این مدارها تغییر دهیم، نقطه‌ای  خواهد بود که در آن، مقدار راکتانس خازنی با راکتانس القایی برابر خواهد و  بنابراین XC=XL.

به نقطه فرکانسی که در آن این اتفاق رخ می‌دهد؛ تشدید گفته می‌شود و در مقاله بعدی، به تشدید سری و این‌که چگونه حضور آن در تغییر مشخصات مدار نقش دارد؛ خواهیم پرداخت.