نمودار های فازوری

نمودار های فازوری، یک راه گرافیکی برای نمایش‌دادن رابطه اندازه و جهت، میان دو یا چند مقدار متناوب است.

شکل‌ موج‌های سینوسی هم‌ فرکانس، می‌توانند یک اختلاف فاز در بین خود داشته باشند؛ که نشان‌دهنده‌ی اختلاف زاویه‌ای بین دو شکل‌موج  سینوسی است. هم‌چنین، اصطلاحات “جلوبودن”(lead) و “عقب ماندن” (lag) و نیز  “هم‌فاز” (in-phase) و “خارج‌از فاز” (out-of-phase) معمولا، برای  نشان‌دادن رابطه‌ی یک شکل‌موج با دیگری، با بیان سینوسی تعمیم‌ داده‌شده به  صورت  بیان می‌شود و نشان‌دهنده موج سینوسی در حوزه زمان است.

اما  زمانی‌که، این روش به صورت ریاضی ارائه می‌شود؛ گاهی متصور ساختن تفاوت  زاویه‌ای یا فازوری بین دو یا چند شکل‌موج سینوسی دشوار است. یکی از  راه‌های غلبه براین مشکل، نمایش‌دادن گرافیکی موج سینوسی در حوزه فضایی یا  فازوری با استفاده از نمود‌ار‌های فازوری است و این امر، با روش بردار دوار حاصل می‌شود.

اساسا یک بردار دوار، که به سادگی “فازور”  خوانده می‌شود؛ خط مقیاسی است که طول یک کمیت (مقدار) AC را نشان می‌دهد و  دارای هم اندازه “دامنه پیک” و هم جهت “فاز” است که در یک نقطه از زمان  “بی حرکت” مانده‌است.

فازور، برداری است که در انتهای یک سر آن، فلشی  وجود دارد که یک بخش آن، نشان ‌دهنده حداکثر مقدار بردار (V یا I) بوده و  بخش دیگر آن، انتهای بردار است که دوران می‌یابد.

به طور‌کلی، فرض  می‌شود که بردارها در یک انتها، حول یک نقطه صفر ثابت، معروف به “نقطه  مبدا” دوران می‌یابند؛ در حالی‌که، انتهای پیکان‌دار، نشان‌دهنده‌ کمیتی  است که آزادانه در خلاف جهت عقربه‌های ساعت با سرعت زاویه‌ای (ω)، یک دوران کامل را برای هر سیکل خواهد داشت.

اگرچه،  هردو اصطلاح بردار و فازور برای توصیف کردن یک خط دورانی است که دارای  اندازه و جهت است؛ تفاوت اصلی بین این دو، این است که؛ اندازه بردار، در  واقع “مقدار پیک” یک موج سینوسی است؛ در حالی‌که، اندازه یک فازور، “مقدار rms” یک موج سینوسی را بیان می‌کند. اما در هر دو مورد، زاویه فاز و جهت یکسان باقی می‌ماند.

فاز  یک مقدار متناوب در هر لحظه‌ای از زمان را، می‌توان با یک نمودار فازوری  نشان داد. بنابراین، نمودارهای فازوری را می‌توان به عنوان “توابع زمانی”  در نظر گرفت. یک موج سینوسی کامل را می‌توان با یک بردار تنها که با سرعت  زاویه‌ای  دوران می‌یابد، در جایی‌که f فرکانس شکل‌موج است؛ ساخت. در  نتیجه، فازور کمیتی است که هم دارای “اندازه” و هم “جهت”  است. در حالت کلی، هنگام ساختن نمودار فازور، سرعت زاویه‌ای یک موج سینوسی  (ω) همیشه برحسب  rad/secفرض می‌شود. نمودار فازوری زیر را در نظر بگیرید:

نمودار فازوری یک شکل‌موج سینوسی

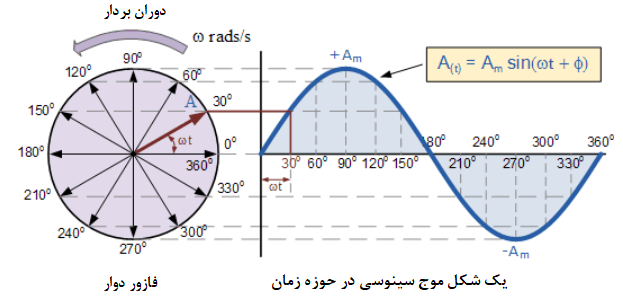۱. نمودار فازوری یک شکل‌موج سینوسی

زمانی‌که یک بردار منفرد در جهت خلاف عقربه‌های ساعت می‌چرخد،  نوک آن در نقطه A یک دوران کامل، 360° یا 2π را نشان می­دهد که معادل یک  سیکل کامل است. اگر طول نوک متحرک آن، در فواصل زمانی مختلف زاویه‌ای، به  نمودار، مطابق شکل بالا منتقل شود، شکل موج سینوسی از سمت چپ با زمان صفر  رسم می‌شود.

هر موقعیتی در امتداد محور افقی، زمان سپری شده از زمان  صفر (t=0) را نشان می‌دهد. وقتی‌که بردار افقی باشد؛ نوک بردار زاویه‌ها  را در 0°، 180° و 360° نشان می‌دهد. به همین ترتیب، وقتی نوک بردار عمودی  باشد، نشان‌دهنده مقدار پیک مثبت (Am+) در 90° یا π/2 و مقدار پیک منفی  (Am-) در 270° یا 3π/2 است. سپس محور زمانی شکل‌موج، زاویه را به صورت درجه  یا رادیان نمایش می‌دهد که فازور از طریق آن حرکت کرده‌است. بنابراین  می‌توان گفت که یک فازور، مقدار ولتاژ یا جریان مقیاس‌پذیر یک بردار دوار  را نشان می‌دهد که در مقطعی از زمان”بی‌حرکت” مانده است و در مثال ما در  بالا، این در زاویه 30° است.

گاهی‌اوقات، هنگامی‌که در حال تجزیه و  تحلیل شکل‌موج‌های سینوسی متناوب می‌باشیم؛ ممکن است نیاز به دانستن موقعیت  فازور داشته‌باشیم، درنتیجه، مقدار متناوب را در یک لحظه‌ی خاص در زمان  نشان می‌دهیم، به ویژه، هنگامی که می‌خواهیم دو شکل‌موج مختلف را در یک  محور مقایسه کنیم؛ برای مثال: ولتاژ و جریان.

ما در شکل‌موج بالا فرض  کردیم که شکل‌موج در زمان t=0 با یک زاویه فاز، برحسب درجه یا رادیان قرار  دارد. اما، اگر شکل‌موج دوم از سمت چپ یا راست این نقطه صفر شروع شود؛ یا  بخواهیم رابطه بین دو شکل‌موج را در نت فاز نشان دهیم، باید این اختلاف فاز  ( φ )، شکل‌ موج را در نظر بگیریم. نمودار زیر را که در مقاله قبلی اختلاف فاز دیدید، در نظر بگیرید.

اختلاف فاز یک شکل‌موج سینوسی

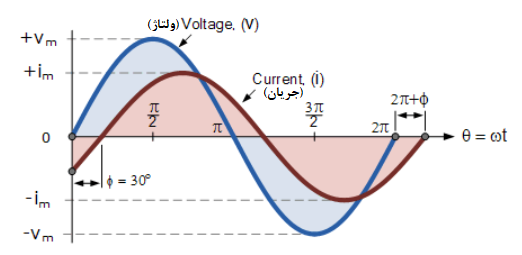۲. اختلاف فاز یک شکل‌موج سینوسی

عبارت ریاضی تعمیم‌یافته برای تعریف این دو مقدار سینوسی به صورت زیر نوشته می‌شود:

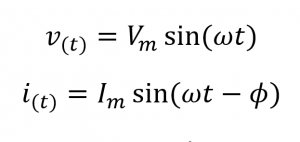
جریان (i) از ولتاژ (v) عقب مانده است. v با زاویه φ و در مثال ما در بالا برابر با 30° است. بنابراین تفاوت بین دو فازور نشان‌دهنده‌ی دو مقدار سینوسی، زاویه φ بوده و نمودار فازور آن به صورت زیر است:

شکل‌ موج سینوسی یک نمودار فازوری

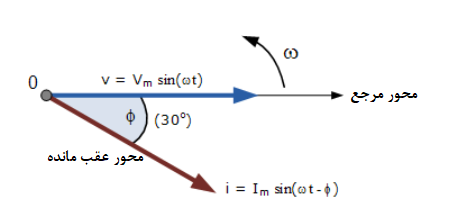۳. شکل‌ موج سینوسی یک نمودار فازوری

نمودار فازوری برحسب زمان صفر (t=0) بر محور افقی ترسیم شده است.  طول فازور‌ها، متناسب با مقادیر ولتاژ (I) و جریان (V) در لحظه‌ای از زمان  است؛ که نمودار فازور در آن رسم گشته‌است. فازور جریان از فازور ولتاژ با  زاویهφ، عقب می‌ماند؛ زیرا دو فازور در جهت خلاف عقربه های ساعت همانطور که  قبلا گفته شد دوران می‌کنند؛ بنابراین زاویه φ، در همان جهت خلاف عقربه  های ساعت، اندازه‌گیری می‌شود.

اگر، با این حال، شکل‌ موج‌ها در زمان  بی‌حرکت بمانند (t=30°)، نمودار فازوری مربوطه ،همان شکلی است که در سمت  چپ نشان ‌داده شده‌است. یک بار دیگر، فازور جریان، در پشت فازور ولتاژ  می‌ماند؛ و هر دو شکل‌موج هم‌فرکانس می‌باشند.

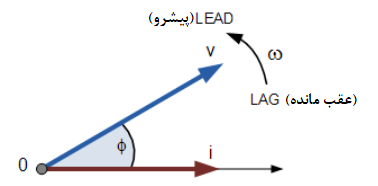۴. نمودار فازوری برحسب زمان

با این حال، چون شکل‌موج جریان، در حال عبور از خط افقی محور صفر  در این لحظه است؛ می‌توانیم از فازور جریان، به عنوان مرجع جدید خود  استفاده کنیم و به درستی بگوییم که فازور ولتاژ “پیشرو” تر از فازور جریان  با زاویه φ است. در هر صورت، یک فازور، به عنوان فازور مرجع تعیین می‌شود و  سایر فازور‌ها با توجه به این مرجع، یا پیشرو (Lead) و یا عقب مانده (Lag)  می‌باشند.

جمع فازور

گاهی‌اوقات، هنگام مطالعه‌ی موج‌های سینوسی، لازم است که دو شکل‌موج متناوب، به عنوان مثال در مدار سری AC، که  با یکدیگر هم‌فاز نیستند، با هم جمع گردند. اگر آن‌ها هم‌فاز باشند، هیچ  تغییری در فاز وجود ندارد، بنابراین می‌توان آن‌ها را به همان روش مقادیر  DC برای یافتن مجموع جبری دو بردار به هم اضافه کرد.

به عنوان مثال، اگر دو ولتاژ ، 50V و 25V به ترتیب باهم “هم‌فاز” باشند، بایکدیگر جمع شده و یک ولتاژ 75V(50+25) را تشکیل می‌دهند.

اگر  هم‌فاز نباشند، یعنی جهت یا نقطه شروع یکسانی ندارند، و باید زاویه فاز  بین آن‌ها در نظر گرفته شود، بنابراین با استفاده از نمودارهای فازوری به  یکدیگر اضافه می‌شوند تا فازورحاصل یا جمع برداری آن، با استفاده از قانون متوازی الاضلاع حاصل شود.

دو ولتاژ AC، را در نظر بگیرید که V1 دارای پیک ولتاژ در 20 ولت بوده و V2 دارای پیک  ولتاژ در 30 ولت است، و V1 از V2،60° پیشروتر است. ولتاژکل (VT)  دو ولتاژ را می‌توان با ترسیم یک نمودار فازوری نشان‌دهنده‌ی دو بردار و  سپس ساخت یک موازی دو طرف دو ولتاژ ایجاد نمود، دو ولتاژ V1 و V2 به صورت  زیر است:

جمع فازوری دو فازور

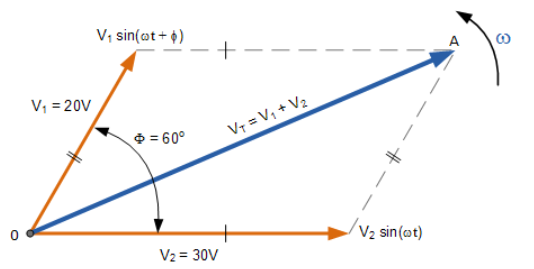۵. جمع فازوری

با ترسیم دو فازور برای مقیاس‌گذاری روی کاغذ گراف، می‌توان  مجموع فازور آن‌ها V1+V2 را به راحتی و با اندازه‌گیری طول خط مورب، معروف  به “بردار حاصل r ” از نقطه صفر تا ساختار خطوط 0 تا A به دست آورد. نکته  منفی این روش گرافیکی، این است که رسم فازورها در مقیاس مربوطه، زمان‌بر  است.

به علاوه، با وجود این‌که این روش گرافیکی پاسخی را ارائه  می‌دهد، که برای اکثر اهداف، به اندازه کافی دقیق است؛ اگر به طور دقیق یا  صحیح برای مقیاس کشیده نشود، ممکن سبب ایجاد خطا گردد. درنتیجه، یک روش  برای اطمینان از همیشه صحیح بودن پاسخ، روش تحلیلی است.

از نظر  ریاضی، می‌توان دو ولتاژ را با یافتن جهت عمودی و افقی آن و سپس محاسبه  نمودن مولفه های عمودی و افقی، برای یافتن بردار حاصل r، VT، با یکدیگر جمع نمود. این روش تحلیلی را که از قاعده‌ی کسینوس و سینوس برای یافتن مقدار حاصل استفاده می‌کند؛ معمولا روش مستطیل می‌نامند.

در فرم مستطیل، فازور را میتوان به یک بخش حقیقی x و بخش دیگر موهومی y تقسیم‌بندی کرد. y شکل بیان کلی  را تشکیل می‌دهد. ( در مقاله بعدی، جزئیات بیشتری در مورد  این بحث را ارائه خواهیم نمود). این یک بیان ریاضی را مطرح می نماید که  نشان‌دهنده‌ی اندازه و فاز ولتاژ سینوسی است:

تعریف یک موج ‌سینوسی پیچیده

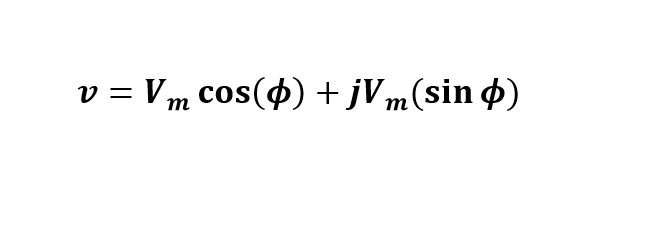
بنابراین، جمع دو بردار A و B با استفاده از عبارت تعمیم یافته قبلی به صورت زیر است:

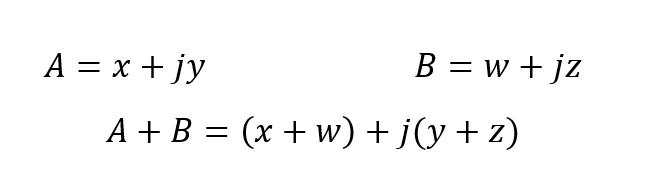
جمع فازوری با استفاده از فرم مستطیلی

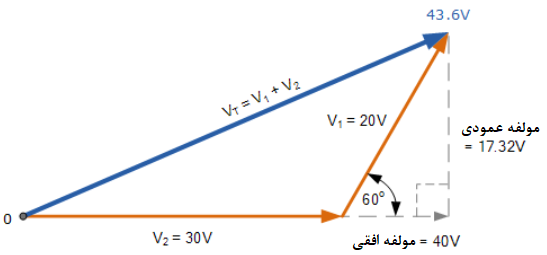
ولتاژ V2،که برابر با ۳۰ ولت است، در امتداد محور صفر  افقی و جهت مرجع قرار دارد، و دارای یک مولفه افقی است؛ در صورتی‌که هیچ  مولفه عمودی ندارد.

• مولفه‌ی افقی = 30cos0°=30 ولت
• مولفه‌ی عمودی = 30sin0°=0 ولت

در نتیجه بیان مستطیلی ولتاژ V2 به صورت: 30+j0 خواهد بود.

ولتاژ V1،که برابر با ۲۰ ولت است، و با زاویه ۶۰° ،پیشروتر از V2 است. دارای دو مولفه افقی و عمودی به صورت زیر است.

• مولفه‌ی افقی = 20cos60°=20*0.5=10 ولت
• مولفه‌ی عمودی = 20sin60°=20*0.866=17.32 ولت

در نتیجه بیان مستطیلی ولتاژ V2 به صورت: 10+j17.32 خواهد بود.

ولتاژ حاصل VT را می‌توان با جمع‌کردن مولفه های افقی و عمودی با یکدیگر به دست آورد.

اکنون که مقادیر حقیقی و موهومی ولتاژ حاصل شده است. VT به سادگی با استفاده از قضیه فیثاغورث یک مثلث ۹۰° ،به صورت زیر تعیین می‌شود.

درنتیجه، نمودار فازور حاصل به صورت زیر خواهد بود:

تفریق فازور

تفریق فازور، شباهت زیادی به روش جمع مستطیلی فوق دارد، با این  تفاوت که این‌بار، اختلاف بردار مورب دیگری از متوازی الاضلاع بین دو ولتاژ  V1 و V2 نشان داده شده‌است.

تفریق برداری دو فازور

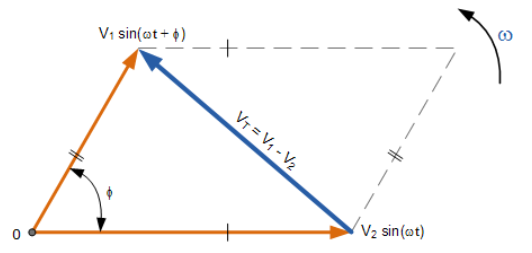۶. تفریق برداری دو فازور

این‌بار به جای آن که مولفه‌های افقی و عمودی را جمع کنیم؛ آن‌ها را از یکدیگر تفریق می‌نماییم.

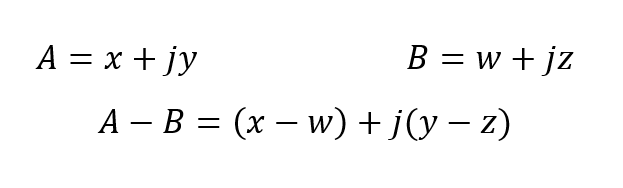
نمودار ۳ فازی فازور

پیش از این، ما فقط به شکل‌موج‌های تک فاز AC پرداختیم؛ که در آن  یک کویل مولتی ترن، در یک میدان مغناطیسی دوران می‌یابد. اما اگر سه کویل  یکسان با تعداد ترن (چرخش) یکسان کویل، در یک زاویه الکتریکی 120° نسبت به  یکدیگر بر روی یک شفت روتور قرار بگیرند، یک منبع تغذیه ولتاژ سه فاز ایجاد  می‌شود.

یک منبع تغذیه ولتاژ سه‌فاز متعادل، از سه ولتاژ سینوسی  جداگانه تشکیل شده‌است؛ که از نظر اندازه و فرکانس، با یکدیگر برابر بوده  اما دقیقا ۱۲۰° درجه الکتریکی، اختلاف فاز دارند.

روش استاندارد این است که، سه مرحله را به صورت قرمز، زرد و آبی کدگذاری کنید تا هر مرحله به درستی مشخص شود. مرحله قرمز به عنوان مرحله  مرجع در نظر گرفته می‌شود. توالی عادی دوران برای یک منبع سه ‌فاز، قرمز ، پس از آن زرد و پس از آن آبی است(R,Y,B).

همانند  فازور‌های تک‌فاز بالا، فازورهای نمایانگر یک سیستم سه‌فاز نیز، در جهت  خلاف جهت عقربه‌های ساعت، به دور یک نقطه مرکزی دوران می‌کنند؛ که با یک  پیکان مشخص‌شده در rad/s مشخص شده است. فازور‌های مربوط به یک سیستم متوازن  ستاره‌ای یا دلتا سه فاز در زیر نشان‌داده شده است.

نمودار سه فازی فازور

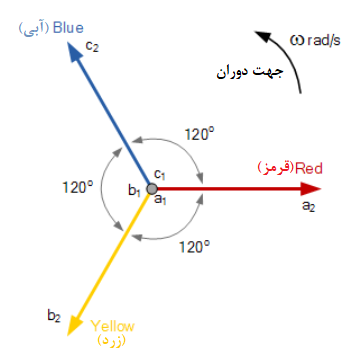۷. نمودار سه فازی فازور

ولتاژ‌های فاز، از نظر اندازه برابر بوده و فقط در زاویه‌ی ‌فاز متفاوت می‌باشند. سه سیم‌پیچ (windings) کویل‌ها در نقاطa1، b1، c1  به هم متصل شده؛ تا یک اتصال خنثی مشترک، برای سه مرحله جداگانه ایجاد  کنند. اگر فاز قرمز، به عنوان فاز مرجع در نظر گرفته شود؛ هر ولتاژ جداگانه  را می‌توان با توجه به اتصال خنثی مشترک تعریف کرد.

معادلات ولتاژ سه فاز

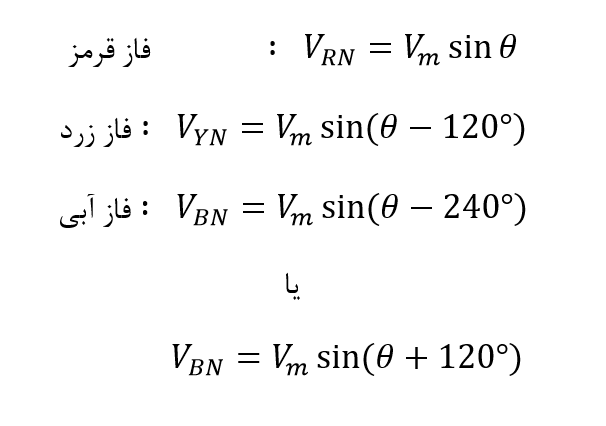
اگر ولتاژ فاز قرمز (VRN)، به عنوان ولتاژ مرجع در نظر گرفته شود؛ همانطور که قبلا گفته شد؛ توالی فاز R–Y–B خواهد بود. بنابراین ولتاژ در فاز زرد (VYN)، از (VRN) ۱۲۰° عقب می‌ماند و (VYN) از (VBN) ۱۲۰° عقب می‌ماند اما هم‌چنین می‌توان گفت که ولتاژ فاز آبی، ( VBN) ۱۲۰° از (VRN) پیشروتر است.

نکته  نهایی در مورد سیستم‌های سه فاز؛ این است که، از آن‌جایی که سه ولتاژ  سینوسی جداگانه، دارای یک رابطه ثابت ۱۲۰° بوده؛ گفته می‌شود که متعادل  می‌باشند. بنابراین، در مجموعه‌ای از ولتاژهای سه فاز متعادل، مجموع  فازورهای آن‌ها همیشه صفر خواهد بود.

خلاصه نمودار فازور

اگر بخواهیم کمی آموزش نمودارهای فازوری را خلاصه کنیم:

در  ساده‌ترین اصطلاحات موجود، نمودارهای فازوری، برآوردی از یک بردار دوار  بر‌روی یک محور افقی می‌باشند؛ که مقدار لحظه‌ای را نشان‌ می‌دهند. همانطور  که یک نمودار فازوری، قادر به نمایش‌دادن هر لحظه‌ای از زمان و بنابراین  هر زاویه‌ای نیز می‌باشد؛ فازور مرجع یک مقدار متناوب، همیشه در جهت مثبت  محور x ترسیم می‌شود.

• بردارها، فازورها و نمودارهای فازوری، تنها، به مقادیر متناوب موج سینوسی اعمال می‌شوند.
• یک نمودار فازوری را، می‌توان برای نشان دادن دو یا چند مقدار سینوسی در هر لحظه از زمان، استفاده نمود.
• در  حالت کلی، فازور مرجع در امتداد محور افقی رسم می‌شود و در آن لحظه،  بقیه‌ی فازورها ترسیم می‌شوند. همه‌ی فازورها به محور صفر، ارجاع داده  می‌شوند.
• نمودارهای فازوری، می‌توانند بیش از دو موج سینوسی را  نشان دهند. آن‌ها می‌توانند، ولتاژ، جریان یا مقدار متناوب دیگری باشند اما  فرکانس همه آن‌ها، باید یکسان باشد.
• تمام  فازورها، در جهت خلاف جهت عقربه‌های ساعت دوران می‌یابند. به تمام فازورهای  جلوتر از فازور مرجع، “پیشرو” و به تمام فازورهای عقب‌مانده از فازور  مرجع، “عقب مانده” گفته می‌شود.
• در حالت کلی، طول یک فازور نشان‌دهنده‌ی m.s است که برابر با مقدارکمیت سینوسی به جای حداکثر مقدار آن است.
• موج‌های  سینوسی با فرکانس‌های مختلف، به دلیل سرعت متفاوت بردارها؛ نمی‌توانند در  یک نمودار فازوری یکسان، نمایش داده شوند. در هر لحظه از زمان، فاز بین  آن‌ها، متفاوت خواهد بود.
• می‌توان دو یا چند بردار را با هم جمع، یا از یک‌دیگر تفریق نمود که در نهایت یه یک بردار منفرد، تبدیل می‌گردد که به آن، بردار حاصل می‌گویند.
• بخش  افقی بردار، برابر بخش حقیقی یا x و بخش عمودی بردار، برابر با بخش موهومی  یا y است. وتر مثلث زاویه‌دار حاصل، برابر با بردار r است.
• در یک سیستم متعادل سه فاز، هر فاز جداگانه با زاویه ۱۲۰° جابه‌جا می‌شود.

درمقاله  بعدی در مورد تئوری‌های AC، نگاهی به نمایش شکل‌موج های سینوسی به صورت  اعداد مختلط، فرم مستطیلی، فرم قطبی و نمایی خواهیم داشت.