اصلاح ضریب توان

اصلاح ضریب توان، روشی است که از خازن‌ها برای کاهش جز توان راکتیو در مدار AC، به منظور بهبود کارایی و کاهش جریان استفاده می‌کند.

هنگام  سروکار داشتن با مدارهای جریان مستقیم (DC)، توان تلف شده توسط بار متصل،  به‌سادگی توسط حاصل ضرب ولتاژ DC در جریان DC به‌دست می‌آید که حاصل V*I بر  حسب وات (W) است. برای یک بار مقاومتی ثابت، جریان، متناسب با ولتاژ  اعمالی بوده و از این رو، توان الکتریکی، توسط بار مقاومتی به‌صورت خطی تلف  می‌گردد. اما در یک مدار جریان متناوب (AC)، موقعیت متفاوت است؛ زیرا  راکتانس بر رفتار مدار تاثیر می‌گذارد.

برای یک مدار AC، توان تلف  شده برحسب وات در هر لحظه، برابر با حاصل ضرب ولت در آمپر، در همان لحظه  ‌بوده و دلیل آن، ولتاژ (و جریان) سینوسی است؛ بنابراین به‌طور مداوم،  تغییر در اندازه و جهت همراه با زمان و با نرخ تعیین‌شده توسط فرکانس منبع صورت می‌پذیرد.

در  یک مدار DC، توان متوسط به سادگی برابر با V*I است؛ اما توان متوسط یک  مدار AC، به‌دلیل حضور تعداد زیادی بار AC، مانند کویل‌ها، سیم‌پیچ‌ها،  ترانسفورماتورها و … نمی‌تواند همان مقدار باشد. در جایی که، جریان دارای  اختلاف فازی بر حسب چند درجه با ولتاژ بوده که در نتیجه توان واقعی تلف شده  برحسب وات، و کمتر از حاصل ضرب ولتاژ و جریان است. و دلیل آن، حضور هم  رزیستانس و هم راکتانس و زاویه‌فاز (θ) بین آن‌ها بوده که حتما باید در نظر  گرفته‌شود.

در آموزش مربوط به شکل‌موج‌های سینوسی،  زاویه‌فاز (∠θ)، زاویه‌ای برحسب درجه الکتریکی بوده که درآن جریان از  ولتاژ عقب می‌ماند. برای یک بار کاملا مقاومتی، ولتاژ و جریان “همفاز”  بوده؛ زیرا که راکتانسی وجود ندارد.

با این حال، برای یک مدار AC حاوی سلف، کویل یا سلونوئید یا یک شکل دیگری از بار القایی، راکتانس القایی (XL)، زاویه فازی ایجاد کرده، که جریان با زاویه 90° عقب‌تر از ولتاژ است. بنابراین رزیستانس (R) و راکتانس القایی (XL) که هر دو برحسب اهم می‌باشند، اثر ترکیبی به نام امپدانس را ایجاد می‌کنند. پس امپدانس که با نماد Z نمایش داده می‌شود، مقدار  حاصله‌ای برحسب اهم بوده ،که ناشی از اثر ترکیبی رزیستانس و راکتانس مدار  است.

مدار سری RLC را در نظر بگیرید:

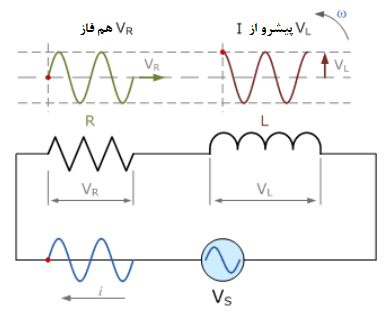
مدار RL سری

از آنجایی‌که مدار سری می‌باشد جریان باید بین مقاومت و سلف مشترک باشد، از این رو، افت ولتاژ دو سر مقاومت، VR هم فاز با جریان سری بوده؛ در حالی که افت ولتاژ دو سر سلف، VL،  از جریان 90° پیشروتر است (ELI). درنتیجه، افت ولتاژ دو سر مقاومت، بر روی  بردار جریان کشیده می‌شود؛ زیرا هر دو بردار همفاز بوده، اما، ولتاژ دو سر  کویل القایی در جهت عمودی کشیده شده، زیرا ولتاژ از جریان با زاویه   90°جلوتر است.

بنابراین، نمودار برداری کشیده‌شده برای هر عنصر،  دارای بردار جریان به‌عنوان مرجع خود بوده و دو بردار ولتاژ با توجه به  موقعیت خود، نسبت به آن رسم می‌گردند و در شکل زیر نشان داده‌شده‌است.

نمودارهای برداری R و L

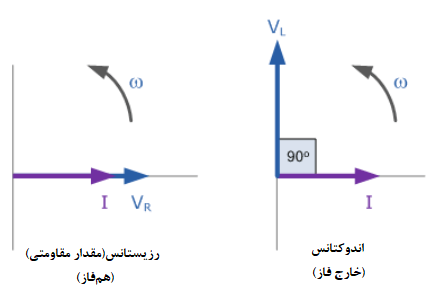
ولتاژ مقاومت VR، در امتداد محور افقی یا “محور حقیقی” و ولتاژ سلف VL در امتداد محور عمودی یا “محور موهومی” رسم می‌شود. برای یافتن ولتاژ حاصل VS در مدار اتصال سری، باید دو بردار مجزا را با یکدیگر، در حالی که بردار  جریان مرجع است؛ ترکیب کنیم. ولتاژ عمودی حاصل می‌تواند به آسانی توسط قضیه  فیثاغورث، به دلیل‌اینکه ترکیب VR و VL یک زاویه قائمه را تشکیل‌ می‌دهند، به‌صورت زیر نشان داده‌شود.

نمودار فازوری برای مدار سری RL

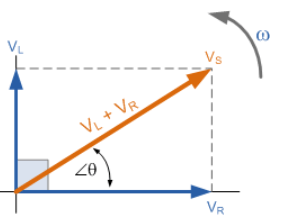
جمع برداری VR و VL، نه تنها دامنه VS را از طریق معادله فیثاغورت، بلکه زاویه‌فاز حاصل (∠θ) بین VS و i را نیز در اختیار ما قرار می‌دهد، که می‌توان از هر یک از توابع  مثلثاتی استاندارد: سینوس، کسینوس یا تانژانت برای یافتن آن، استفاده کرد.

مثال ۱

در یک مدار سری RL، متشکل از رزیستانس 15Ω و سلف با اندوکتانس  القایی 26Ω، اگر جریان جاری در مدار برابر با 5 آمپر باشد. محاسبه کنید:

1.  ولتاژ منبع تغذیه
2.  زاویه فاز بین ولتاژ منبع و جریان مدار
3.  نمودار فازور حاصل را نیز رسم کنید.
4. ولتاژ منبع تغذیه VS

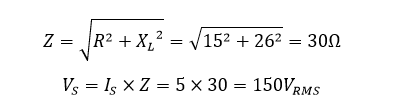
می‌توانیم پاسخ 150Vrms را با استفاده از امپدانس مدار به‌صورت زیر، دوباره چک کنیم:

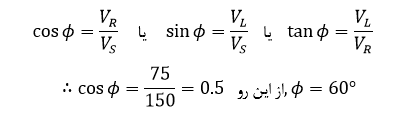
۲. زاویه فاز (θ) با استفاده از تابع مثلثاتی خواهد بود:

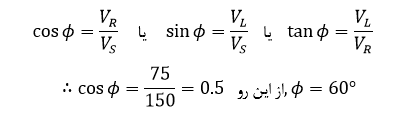
۳. نمودار فازور حاصل نشان‌دهنده‌ی VS

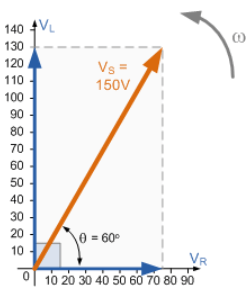
افت ولتاژ محاسبه شده دو سر مقاومت  (جز حقیقی) برابر ۷۵ ولت بوده؛ در حالیکه، ولتاژ تولید‌ شده دو سر سلف (جز  موهومی) برابر با ۱۳۰ ولت است. روشن است که مجموع ۷۵ ولت با ۱۳۰ ولت برابر  با ۲۰۵ ولت است. این مقدار از مقدار محاسبه‌شده‌ی ۱۵۰ ولت بزرگتر می‌باشد.  این امر، ناشی از این واقعیت است که مقدار ۱۵۰ ولت نشان دهنده‌ی مجموع  فازوری است. با دانستن افت ولتاژ و امپدانس‌های منفرد، می‌توانیم این  مقادیر را به مقادیری تبدیل کنیم که توان مصرفی، حقیقی یا موهومی را به ما  نشان دهند.

توان در مدار سری RL

در یک مدار شامل راکتانس، جریان i، مقداری پیشرو تر یا عقب‌مانده  تر از ولتاژ، براساس خازنی یا القایی بودن راکتانس خواهد بود. توان مصرفی  بر حسب وات توسط مقاومت را توان واقعی نامیده که نماد آن P یا W است. وات  همچنین می‌تواند از طریق I۲R، در جایی که R، رزیستانس کل مدار  است محاسبه گردد. در هر حال، برای محاسبه مقدار توان واقعی، با استفاده از  Vrms و Irms (ضرب آن‌ها در هم) باید این مقادیر را در کسینوس زاویه‌فاز  (cos(θ)) نیز ضرب کنیم:

همانطور که در بالا دیدیم؛ ولتاژ و جریان برای یک رزیستانس هم  فاز بوده، زیرا زاویه فاز برابر با 0 (صفر) است و cos(θ)=1 را در اختیار ما  قرار می‌دهد. ضرب V*I*1، به ما  همان مقدار توان واقعی، ناشی از I۲R را خواهد داد. پس با استفاده از مثال کویل بالا، توان تلف‌شده در مقاومت 15Ω خواهد بود:

که دقیقا برابر است با:

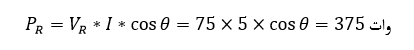
زمانی که، ولتاژ و جریان دارای “اختلاف فاز با یکدیگر”، به دلیل  راکتانس مدار می‌باشند، حاصل‌ضرب V*I برابر با “توان ظاهری” خواهد بود که  یکای آن ولت آمپرز (VA) به‌جای وات است. ولت آمپرز دارای نماد “S” می‌باشد.  برای یک مدار کاملا القایی، جریان، از ولتاژ با زاویه 90°، عقب‌تر خواهد  بود. بنابراین توان راکتیو برای بار القایی V*I*cos(+90°)خواهد بود که در  نتیجه برابر با V*I*0 است. روشن است که، هیچ توانی توسط اندوکتانس مصرف  نمی‌شود، در نتیجه هیچ از دست دادن توانی هم نخواهیم داشت و PL=0  وات است. اما توان بدون وات موجود در مدار AC، ولت آمپر راکتیو (VAr) نام  دارد و دارای نماد Q”” است. برای ولت آمپر راکتیو یا “توان راکتیو” برای  مدار القایی از نماد QL استفاده می‌نماییم.

مشابه آن برای  مدار کاملا خازنی، جریان، از ولتاژ با زاویه 90°، پیشرو تر خواهد بود.  بنابراین توان راکتیو برای بار خازنی V*I*cos(-90°)می‌شود که در نتیجه  برابر با V*I*0 است. روشن است‌که مانند قبل، هیچ توانی توسط ظرفیت خازنی  مصرف نمی‌شود، در نتیجه هیچ از دست دادن توانی نخواهیم داشت و PC=0 وات است. اما توان بدون وات موجود در مدار خازنی AC، ولت آمپر راکتیو خازنی بوده و دارای نماد “QC” است. توجه داشته باشید که توان راکتیو ظرفیت خازنی به صورت منفی تعریف می‌شود، و به‌صورت -QC نشان داده می‌شود.

پس دوباره، اگر از مثال بالا استفاده کنیم، توان راکتیو جاری در داخل و خارج سلف با نرخ تعیین شده توسط فرکانس خواهد بود:

از آنجایی که، اختلاف فاز 90° بین شکل موج‌های ولتاژ و جریان  برای راکتانس خالص (چه القایی و چه خازنی) وجود دارد، ضرب V*I*sinθ جز  عمودی 90° خارج فاز را خواهد داد. در هر حال، سینوس زاویه (sin90°) برابر  با “1” است؛ پس می‌توانیم توان راکتیو را به سادگی با ضرب ولتاژ rms و  مقادیر جریان به‌صورت زیر بیابیم.

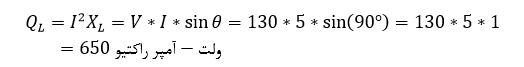
می‌توانیم ببینیم که بخش ولت- آمپر راکتیو یا VAR دارای اندازه (برابر با توان واقعی) بوده؛ اما زاویه فاز مرتبط ندارد. پس توان راکتیو، همیشه بر محور عمودی ۹۰° است. با دانستن روابط زیر:

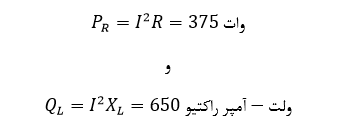
می‌توانیم مثلث توان را برای نمایش رابطه بین P،Q و S بسازیم و خواهیم داشت:

مثلث توان القایی

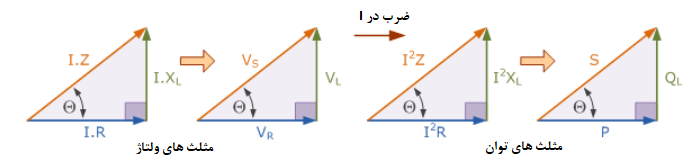مثلث توان القایی

مثلث توان خازنی

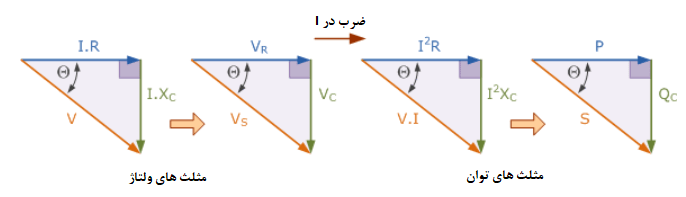مثلث توان خازنی

دوباره می‌توانیم مانند قبل، با استفاده از قضیه فیثاغورث و توابع مثلثاتی سینوس، کسینوس و تانژانت، مثلث توان را تعریف کنیم.

معادلات مثلث توان

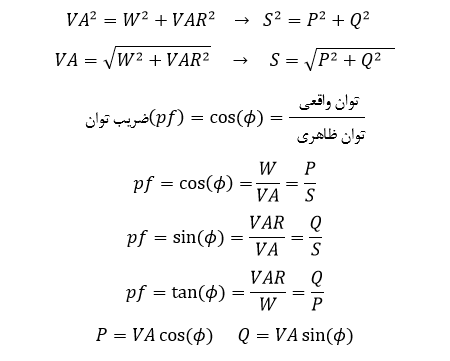
مثال ۲

یک مدار، متشکل از رزیستانس 10Ω و اندوکتانس 46mH است. اگر جریان  جاری در مدار زمانی که متصل به منبع تغذیه  100Vrms,60Hz است برابر با 5  آمپر باشد، محاسبه کنید:

• ولتاژهای دوسر اجزای مدار
• زاویه فاز مدار
• توان‌های متفاوت مصرفی توسط مدارهای سری RL

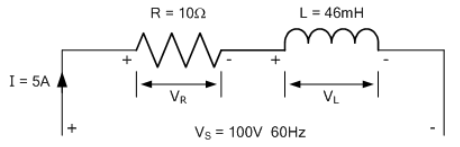
ابتدا امپدانس‌ها را پیدا کرده

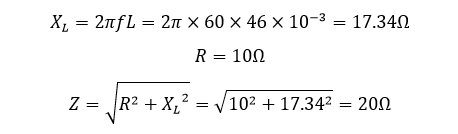
1. ولتاژهای دوسر مقاومت VR و سلف VL

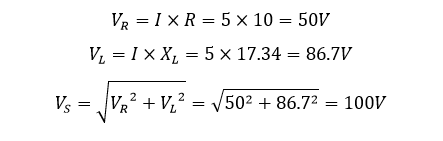
۲. زاویه فاز مدار

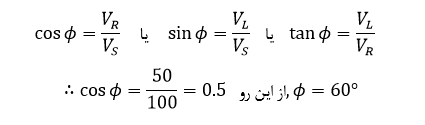
۳. توان مدار

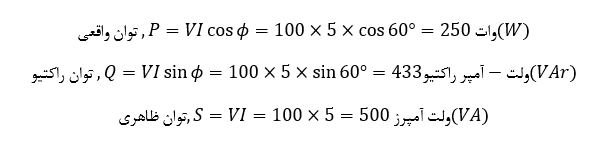
می‌توانیم تایید کنیم که مدار، توان مختلط 500VA را از منبع تغذیه از آن جایی که S=I۲Z و درنتیجه، 5۲*20=500VA است، می‌گیرد و ساخت یک مثلث توان نیز این مطلب را به درستی تایید می‌کند.

توان  مختلط یا توان ظاهری مصرف شده توسط مدار سری RLC از لحاظ مقداری، به‌دلیل  زاویه فاز، بزرگ است و سبب می‌شود ولتاژ از جریان پیشرو تر باشد (ELI). این  مقدار بزرگ نتیجه‌ی ضریب توان کم 0.5 یا cos(60°) است. و نیاز است که  مقداری از توان القایی راکتیومصرفی (433VAr) توسط کویل را؛ برای حفظ میدان  مغناطیسی، با افزودن مقدار بیشتری راکتانس مخالف نوع سیستم به آن، خنثی  کنیم.

آیا باید در مورد ضریب  توان کم کویل‌ها نگران باشیم؟ بله، زیرا ضریب‌توان، نسبت توان واقعی  سیم‌پیچ‌ها به توان ظاهری آن (ولت آمپر/ولت) است و نشان می‌دهد که چگونه  توان الکتریکی به‌طور موثر مورد استفاده واقع می‌شود. بنابراین ضریب توان  کم، به این معنی است که توان الکتریکی تامین شده به‌طورکامل استفاده  نمی‌شود. برای مثال در مثال کویل بالا، در ضریب توان 50% (W/VA=250/500)،  500 ولت آمپر گرفته می‌شود تا 250 وات توان واقعی تولید گردد.

اگر  کویل دارای راکتانس القایی مثبت باشد، پس باید مقداری راکتانس خازنی منفی  برای خنثی کردن آن بیافزایم، که سبب بهبود مقدار کلی ضریب‌توان کویل‌ها  می‌گردد. افزودن خازن‌ها برای کاهش زاویه فاز مدار و مصرف توان راکتیو،  مرتبط با اصلاح ضریب توان است و این امکان را به ما می‌دهد؛ که ضریب توان  مدارها را به واحد یا ۱ نزدیک‌تر کنیم.

اصلاح ضریب توان

تصحیح ضریب توان، سبب بهبود زاویه فاز بین ولتاژ منبع تغذیه و  جریان شده. در حالی که مصرف توان واقعی برحسب وات بدون تغییر می‌ماند. زیرا  راکتانس خالص، هیچ توان واقعی مصرف نمی‌کند. افزودن امپدانس به شکل  راکتانس خازنی به صورت موازی با کویل در بالا، سبب کاهش θ و هم‌چنین افزایش  ضریب توان شده که به نوبه خود سبب کاهش جریان rms گرفته شده از منبع تغذیه  می‌گردد.

ضریب توان یک مدار AC، بسته به قدرت بار القایی می‌تواند  بین 0 تا 1 متغیر باشد؛ اما درحقیقت، برای سنگین‌ترین بارهای القایی هرگز  نمی‌تواند کمتر از 0.2 باشد. همانطور که در بالا دیدیم، ضریب‌توان کمتر از 1  به‌معنای مصرف توان راکتیو بوده که تا نزدیک کردن آن به صفر (کاملا  القایی) افزایش می‌یابد. روشن است‌که ضریب توان دقیقا برابر با 1، به‌معنای  این است که مدار توان راکتیو صفر مصرف می‌کند (کاملا مقاومتی)، در نتیجه،  زاویه ضریب توان 0° بوده و سبب “ضریب توان واحد” می‌گردد.

افزودن  خازن موازی با کویل، نه تنها باعث کاهش توان راکتیو ناخواسته می‌گردد؛ بلکه  باعث کاهش کل جریان گرفته‌شده از منبع می‌شود. در تئوری خازن‌ها می‌توانند  ۱۰۰% توان راکتیو جبران‌شده مورد نیاز مدار را تامین کنند؛ اما در عمل،  اصلاح ضریب‌توان بین ۹۵% و ۹۸% ( ۰.۹۵ تا ۰.۹۸) معمولا کافی است. پس با  نگاه بر کویل مثال شماره ۲، چه مقداری از خازن، برای بهبود ضریب توان از  ۰.۵ تا ۰.۹۵ نیاز است؟

ضریب توان 0.95 برابربا زاویه‌فاز cos-۱(0.95)=18.2° بوده؛ که مقدار VAR مورد نیاز آن برابر است با:

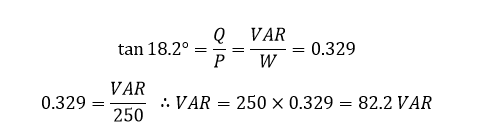
بنابراین، برای زاویه فاز 18.2°، نیاز به مقدار توان راکتیو  82.2VAR است. اگر مقدار اصلاح نشده‌ی اصلی برابر با 433VAR باشد و مقدار  جدید برابر با 82.2VAR؛ نیاز به کاهش 433-82.2=350.8VAR خازنی داریم. از  این‌رو:

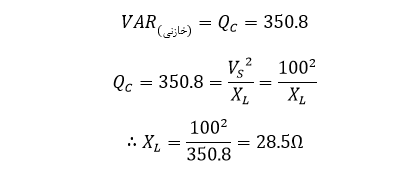
خازن، برای کاهش توان راکتیو تا 82.2VAR ، نیاز به راکتانس خازنی  28.5Ω در نرخ فرکانس منبع‌تغذیه دارد. از این‌رو، ظرفیت خازنی خازن  به‌صورت زیر محاسبه می‌شود:

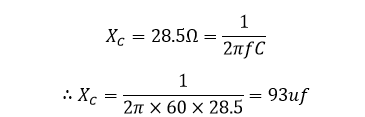
برای بهبود ضریب توان کویل در مثال شماره 2، از 0.5 تا 0.95،  نیاز به خازن موازی متصل شده با مقدار 93uF است. با استفاده از مقادیر  بالا، می‌توان مقدار توان واقعی تامین شده توسط منبع را پس از اعمال تصحیح  ضریب توان، محاسبه نمود.

مقدار جدید ولت آمپرز

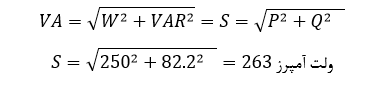
می‌توانیم، یک مثلث توان، برای نشان دادن مقادیر قبل و بعد VA(S) و VAR(Q) به‌صورت زیر بسازیم:

مثلث توان

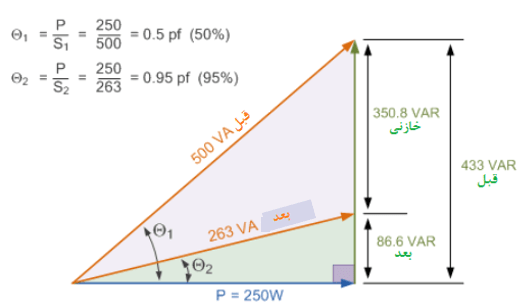
اگر توان ظاهری مدار از 500VA تا 263VA کاهش یابد، می‌توانیم جریان rms تامین شده را بیابیم:

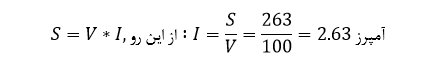
پس اتصال خازن به کویل، نه تنها سبب بهبود ضریب توان کلی از ۰.۵  تا ۰.۹۵ می‌شود؛ بلکه جریان منبع را نیز، از ۵ آمپر به ۲.۶۳ آمپر کاهش  می‌دهد (کاهشی به اندازه ۴۷%).

 مدار نهایی به‌صورت زیر خواهد بود.

مدار نهایی اصلاح ضریب توان

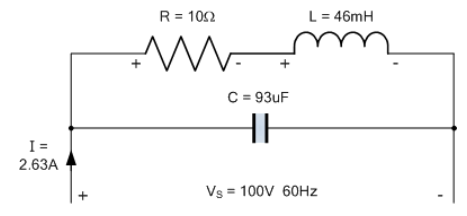
درصورت تمایل می‌توان مقدار خازن را، از مقدار 93uF محاسبه شده،  برای مثال ساده ما، تا مقدار حداکثر 114.8uF افزایش داد؛ که سبب بهبود ضریب  توان از مقدار مورد نیاز 0.95 تا مقدار واحد 1 می‌گردد. در واقعیت، یک  خازن غیر قطبی استاندارد 100uF برای مثال ما مناسب است.

در این آموزش  دیدیم که ضریب‌توان عقب مانده، به‌دلیل بار القایی، سبب افزایش از دست  دادن توان در مدار AC می‌شود. با افزودن عنصر راکتیو خازنی مناسب به شکل  خازن موازی با بارالقایی، می‌توانیم اختلاف فاز بین ولتاژ و جریان را کاهش  دهیم.

این امر  بر ضریب‌توان کم مدار، یعنی نسبت توان فعال به توان  ظاهری، اثر داشته و سبب بهبود کیفیت توان مدار می‌گردد. میزان جریان‌  موردنیاز منبع‌ را نیز کاهش می‌دهد. این روش را “اصلاح ضریب توان”  می‌نامند.