توان در مدار های AC

توان الکتریکی مصرف شده توسط مقاومت در مدار AC، با توان مصرفی در راکتانس متفاوت است؛ زیرا راکتانس انرژی را تلف نمی‌کند.

در  یک مدار DC، توان ‌مصرفی به بیان ‌ساده، محصول ولتاژ DC در جریان DC برحسب  وات است. در حالی ‌که، برای مدار AC، با حضور عناصر راکتیو، نیاز به  محاسبه‌ی توان مصرفی به روش متفاوتی است.

توان الکتریکی؛ “نرخ” مصرف  انرژی در یک مدار است و از این‌رو، تمام عناصر و دستگاه‌های الکتریکی و  الکترونیکی، دارای محدودیتی در مقدار توان الکتریکی می‌باشند؛ که سبب  استفاده بدون خطر آن‌ها در مدار می‌شود. برای مثال، یک مقاومت ۱.۴ وات یا  یک تقویت‌کننده ۲۰ وات.

توان الکتریکی، چه به‌عنوان یک کمیت DC و چه  به‌عنوان یک کمیت AC، می‌تواند متغیر با زمان باشد. مقدار توان الکتریکی در  هر لحظه از زمان در مدار را، توان لحظه‌ای نامیده و با رابطه‌ی  معروف توان برابر است با ضرب ولتاژ در جریان (P=V*I) بیان می‌گردد. پس یک  وات (که میزان مصرف انرژی در یک ژول در ثانیه است) برابر با حاصل ولت-آمپرِ  یک ولت در یک آمپر خواهد بود.

پس توان‌ جذب شده یا تامین شده توسط  یک عنصر مدار، محصول ولتاژ V یک عنصر و جریان I جاری در آن است. بنابراین  اگر یک مدار DC با رزیستانس (مقدار مقاومتی) “R” برحسب اهم داشته باشیم؛  توان اتلاف شده توسط مقاومت برحسب وات، توسط یکی از فرمول‌های کلی زیر بیان  می‌شود:

توان الکتریکی

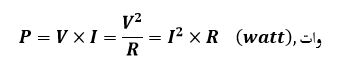
درجایی که: V و I ولتاژ و جریان DC و R مقدار یک رزیستانس است.

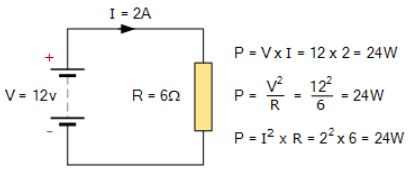
پس  توان در یک مدار الکتریکی، تنها زمانی حضور دارد، که ولتاژ و جریان حاضر  باشند، به این معنا که هیچ وضعیت مدار باز یا مداربسته وجود نداشته باشد.  یک نمونه ساده، از یک مدار استاندارد مقاومتی DC را در نظر بگیرید:

مدار مقاومتی DC

توان الکتریکی در یک مدار AC

در یک مدار DC، ولتاژ ها و جریان ها در حالت کلی، ثابت می‌باشند.  به دلیل این که، هیچ شکل موج سینوسی مرتبط با منبعی وجود ندارد که متغیر  با زمان باشد. اما در یک مدار AC، مقدار لحظه‌ای ولتاژ، جریان و در نتیجه  توان وجود دارد که دائما به دلیل تحت تاثیر منبع تغذیه بودن، تغییر  می‌کنند. پس ‌نمی‌توانیم توان در مدار های AC را به همان روشی که در مدار  های DC محاسبه می‌کردیم، محاسبه نماییم. اما همچنان توان (p) برابر با ضرب  ولتاژ (v) در جریان (i) می‌باشد.

یک نکته مهم دیگر در مورد مدارهای  AC، داشتن راکتانس است؛ یعنی توانی در نتیجه‌ی میدان مغناطیسی و یا  الکتریکی تولیدشده توسط عناصر مدار، تولید می‌شود. در نتیجه، کاملا برخلاف  عنصر مقاومتی، این توان ذخیره شده و سپس به منبع بازگردانده می‌شود؛ در  زمانی که، شکل موج سینوسی از یک سیکل پریودی کامل عبور می‌کند.

بنابراین،  توان متوسط جذب شده توسط مدار، مجموع ذخیره شده و توان برگشتی طی یک سیکل  کامل است. پس میانگین توان متوسط مصرفی مدارها، متوسط توان لحظه‌ای در طی  یک سیکل کامل بوده؛ که این توان لحظه‌ای p، با ضرب ولتاژ لحظه‌ای v در  جریان لحظه‌ای i تعریف می‌شود. توجه داشته‌ باشید که تابع سینوسی پریودیک و  دائمی بوده و توان متوسط در تمام زمان‌ها، دقیقا برابر با توان متوسط طی  یک سیکل تنها است.

اجازه دهید فرض کنیم که شکل موج‌های ولتاژ و جریان هر دو سینوسی بوده و به صورت زیر است:

شکل موج سینوسی ولتاژ

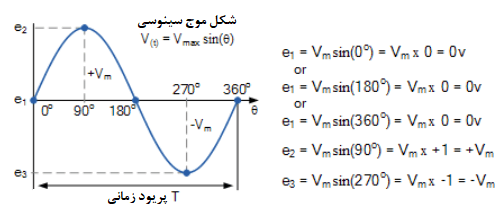
از آن جایی که توان لحظه‌ای، توان هر لحظه‌ از زمان است، داریم:

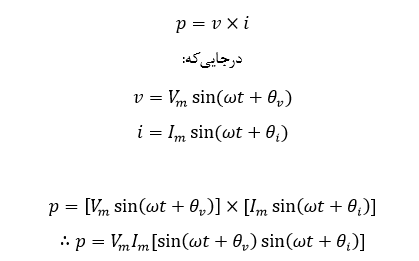
با استفاده از تبدیل مثلثاتی ضرب به جمع داریم:

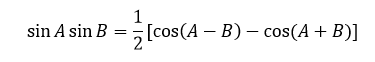
و θ = θv – θi (زاویه‌‌‌ی فاز بین شکل موج های ولتاژ و جریان) که با لحاظ نمودن آن در معادله داریم:

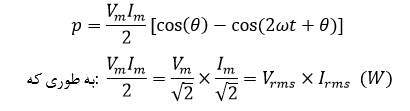
درجایی‌که V و I، به‌ترتیب جذر مربع میانگین (rms) مقادیر شکل  موج های سینوسی v و i بوده و θ اختلاف فاز بین دو شکل موج می‌باشد. از این  رو، می‌توان توان لحظه‌ای را به‌صورت زیر بیان نمود:

معادله‌ی توان لحظه ای AC

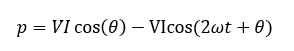
معادله‌ی بالا نشان می‌دهد که توان لحظه ای AC، دو بخش متفاوت  داشته و از این رو، مجموع دو شرط است. شرط دوم، موج سینوسی متغیر با زمان  است؛ که فرکانس آن برابر با دو برابر فرکانس زاویه‌ای منبع تغذیه ناشی از  شرط 2ω است و شرط اول، یک مقدار ثابت بوده که وابسته به اختلاف فاز θ بین  ولتاژ (V) و جریان (I) است.

چون توان لحظه‌ای با گذشت زمان، مداوما  با مشخصات سینوسی در حال تغییر است، اندازه‌گیری آن کمی دشوار می‌شود.  بنابراین استفاده از مقدار متوسط یا میانگین در ریاضیات آسان تر و راحت تر  است. بنابراین، طی تعداد مشخصی از سیکل‌ها، مقدار توان متوسط لحظه‌ای  سینوسی، خواهد بود:

در جاییکه V و I مقادیر سینوسی rms بوده و θ (تتا) زاویه فاز بین ولتاژ و جریان است، یکای توان برحسب وات (W) است.

توان تلف شده AC در مدار را، می‌توان با استفاده از امپدانس (Z) مدار و ولتاژ Vrms یا جریان Irms جاری در مدار مانند زیر نشان داد:

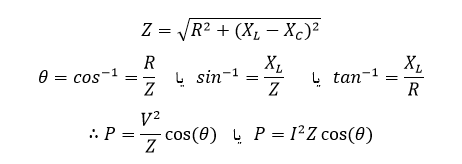
مثال ۱

ولتاژ و جریان یک منبع 50Hz، به ترتیب برابر زیر است، مقادیر توان لحظه‌ای و توان متوسط جذب شده توسط مدار را بیابید.:

vt  = 240×sin(ωt + 60°)

 it = 5×sin(ωt – 10°)

از بالا، توان لحظه‌ای جذب‌شده توسط مدار به‌صورت زیر خواهد بود:

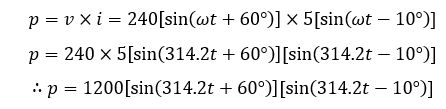
با اعمال نمودن رابطه مثلثاتی بالا خواهیم داشت:

پس:

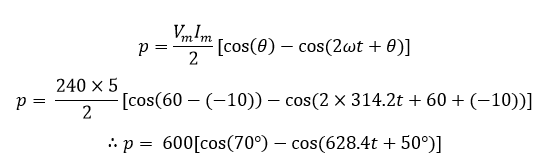
یا:

توان متوسط، به‌صورت زیر محاسبه خواهد شد:

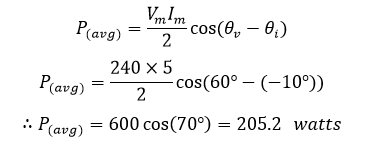
مقدار توان متوسط 205.2 وات، اولین شرط توان لحظه‌ای p(t) نیز می‌باشد. از آن جایی که، شرط اول مقدار ثابت بوده و نرخ انرژی متوسط یا میانگین، تغییر کننده بین منبع و بار است.

توان AC در یک مدار کاملا مقاومتی

تا اینجا مشاهده کردیم؛ که در یک مدار dc، توان برابر با حاصل  ضرب ولتاژ و جریان است و این رابطه‌ برای مدار های کاملا مقاومتی AC، نیز  صادق است. مقاومت‌ها، دستگاه‌های الکتریکی می‌باشند که انرژی را مصرف نموده  و توان در مقاومت با فرمول p = VI = I۲R = V۲/R محاسبه می‌گردد (این توان همواره مثبت است).

مدار  کاملا مقاومتی زیر را (در این مدار خازن بی نهایت C=∞ و اندوکتانس صفر   L=0 است) با یک مقاومت متصل شده به منبع تغذیه AC در نظر بگیرید:

مدار کاملا مقاومتی

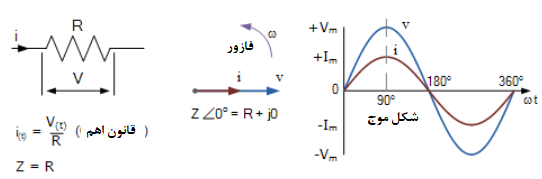
زمانی که، یک مقاومت به یک منبع ولتاژ سینوسی متصل شده باشد؛  جریان عبوری از مقاومت، متناسب با ولتاژ تغذیه تغییر می‌کند. به این معنا  که شکل موج ولتاژ و جریان، با یکدیگر “هم‌فاز” می‌باشند. از این‌رو، اختلاف  فاز میان شکل موج ولتاژ و شکل موج جریان برابر با 0° بوده و زاویه فاز سبب  cos0° شده که برابر با 1 است.

پس توان الکتریکی مصرفی توسط مقاومت خواهد بود:

توان الکتریکی در یک مقاومت خالص

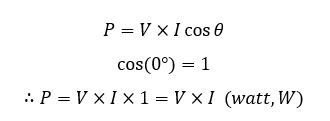
چون که شکل موج‌های ولتاژ و جریان، همفاز می‌باشند؛ هر دو شکل  موج، همزمان به مقادیر پیک خود رسیده و همزمان از صفر عبور می‌کنند،  درنتیجه،معادله توان بالا تا V*I کاهش می‌یابد. از این رو، توان در هر  لحظه، با ضرب دو شکل موج در یکدیگر که محصول ولت-آمپر را به ما می‌دهد؛  به‌دست می‌آید. این‌مقدار را “توان واقعی”(P) نامیده، که برحسب وات (W)، کیلووات (kW) و مگاوات (MW) و … اندازه‌گیری می‌شود.

شکل موج های توان AC در یک مقاومت خالص

نمودار بالا، شکل موج ولتاژ، جریان و توان مربوطه‌ را نشان‌  می‌دهد. به‌دلیل هم فاز بودن ولتاژ و جریان، در طول نیم سیکل مثبت، زمانی  که ولتاژ مثبت بوده، جریان نیز مثبت و در نتیجه توان هم مثبت است؛ زیرا ضرب  مثبت در مثبت، نتیجه مثبت دارد. اما در نیم سیکل منفی، ولتاژ منفی بوده، و  جریان نیز همانند ولتاژ، درنتیجه دوباره توان مثبت خواهد بود. زیرا ضرب  منفی در منفی، مثبت است.

پس در یک مدار کاملا مقاومتی، توان الکتریکی، تمام مدت زمانی که جریان از مقاومت عبور می‌کند، مصرف می‌شود و به صورت P = V*I = I۲R خواهد بود. باید توجه داشت که V و I مقادیر rms بوده، در جاییکه : V = I*R و I = V/R است.

توان AC در یک مدار کاملا القایی

در یک مدار کاملا القایی L برحسب هنری (در این مدار خازن بی  نهایت C=∞ و رزیستانس صفر  R=0است) شکل موج‌های ولتاژ و جریان، همفاز  نمی‌باشند. هر زمان، که ولتاژ متغیر به کویل القایی خالص اعمال شود، یک emf  “معکوس” توسط کویل، به‌دلیل خود القایی تولید می‌شود. خود القایی با هر  تغییری در جریان جاری در کویل، مخالفت کرده و آن را محدود می‌کند.

اثرات  این emf معکوس، این است که جریان نمی‌تواند به سرعت درون کویل هم فاز با  ولتاژ اعمال شده، افزایش یابد و سبب می‌شود که شکل موج جریان، به پیک یا  مقدار حداکثر خود کمی بعد از ولتاژ برسد. نتیجه این است که در مدار القایی  خالص، جریان “عقب‌مانده” (ELI) پشت ولتاژ با 90°(π/2) اختلاف فاز است؛ که  در زیر آمده‌.

مدار کاملا القایی

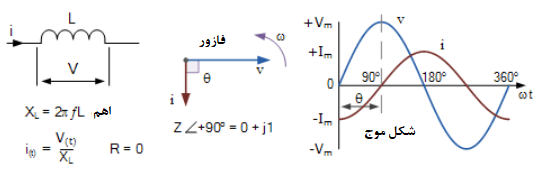
شکل موج های بالا نشان می‌دهد، که ولتاژ لحظه‌ای و جریان لحظه‌ای در یک کویل القایی خالص، تابعی از زمان است. حداکثر جریان Imax در ربع کامل یک سیکل (۹۰°) بعد از حداکثر (پیک) ولتاژ رخ می‌دهد. در بالا،  جریان با حداکثر مقدار منفی خود، در ابتدا سیکل ولتاژ شروع کرده، از صفر  گذشته و به مقدار حداکثر مثبت خود، زمانیکه شکل موج ولتاژ در حداکثر خود در  ۹۰° قرار دارد می‌رسد.

بنابراین، چون شکل موج‌های ولتاژ و جریان،  دیگر با یکدیگر افت و خیر نمی‌یابند و درعوض شیفت فاز (π/2)90° به کویل  وارد می‌شود؛ شکل‌موج‌های ولتاژ و جریان، “خارج از فاز” بوده و ولتاژ 90°  از جریان جلوتر است. از آن جاییکه، اختلاف فاز بین شکل موج ولتاژ و جریان،  90° است، زاویه فاز cos90°=0 را نتیجه می‌دهد.

از اینرو، توان الکتریکی ذخیره شده در سلف خالص، QL برابر است با:

توان واقعی در یک سلف خالص

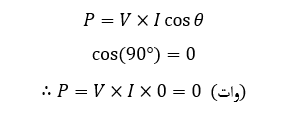
واضح است که، یک سلف خالص هیچ توان حقیقی مصرف یا اتلاف نمی‌کند و  از آنجایی که، ولتاژ و جریان را داریم استفاده از cos(θ) درعبارت P=V*I*  cos(θ) برای یک سلف خالص، دیگر معتبر نیست. محصول جریان و ولتاژ در اینجا  توان موهومی بوده، که عموما “توان راکتیو” (Q)خوانده شده، که برحسب  ولت-آمپر راکتیو (VAr)، کیلو ولت-آمپر راکتیو (kVAr) و … می‌باشد.

ولت-آمپر  راکتیو (VAr) را نباید با وات (W) اشتباه گرفت که برای توان واقعی، به‌کار  برده می‌شود. Var حاصلی از ولت و آمپر هایی با 90° اختلاف فاز است. برای  نمایش توان متوسط راکتیو به صورت ریاضیاتی، تابع سینوسی مورد استفاده قرار  می‌گیرد. پس معادله‌ی توان راکتیو متوسط در سلف خواهد بود:

توان راکتیو در یک سلف خالص

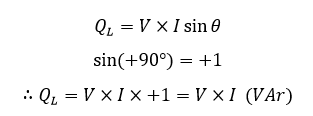
همانند توان واقعی (P)، توان راکتیو (Q)، به ولتاژ و جریان  وابسته است؛ اما به زاویه فاز میان آن‌ها نیز وابسته است. از اینرو، محصول  ولتاژ اعمالی و آن بخش از جریان است؛ که 90° با ولتاژ اختلاف فاز دارد که  در زیر نمایش داده شده است.

شکل موج های توان AC برای یک سلف خالص

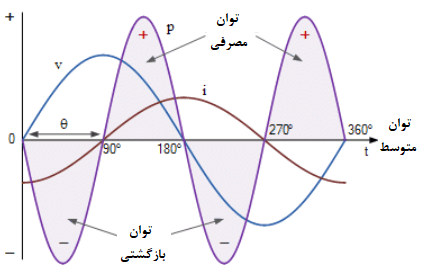
در نیمه مثبت شکل موج ولتاژ بین زاویه ۰° و ۰°۹، جریان سلف، منفی  بوده؛ در‌ حالیکه ولتاژ منبع تغذیه مثبت است. از اینرو، حاصل ولت و آمپر  توان منفی بوده، زیرا منفی در مثبت، منفی می‌شود. بین زاویه ۹۰° و ۱۸۰°، هر  دو شکل موج ولتاژ و جریان مثبت بوده و حاصل، توان مثبت است. توان مثبت،  نشان دهنده‌ی مصرف انرژی الکتریکی کویل از منبع تغذیه است.

در نیمه  منفی شکل موج ولتاژ بین زاویه ۱۸۰° و ۲۷۰°، ولتاژ منفی و جریان مثبت است که  نشان‌دهنده‌ی توان منفی است. توان منفی عنوان می‌کند؛ که کویل انرژی  الکتریکی ذخیره شده را به منبع تغذیه بر می‌گرداند. بین زاویه ۲۷۰° و ۳۶۰°،  جریان سلف و ولتاژ منبع، هر دو منفی بوده، که توان مثبت در این پریود را  نتیجه می‌دهد.

پس در طی یک سیکل کامل شکل موج ولتاژ، دو پالس مثبت و  منفی یکسان داریم؛ که مقدار متوسط آن‌ها صفر است و هیچ توان واقعی استفاده  نمی‌شود زیرا در نهایت توان رفته و به منبع باز می‌گردد. این بدان معناست  که کل توان گرفته شده توسط سلف خالص طی یک سیکل، برابر با صفر است.  بنابراین توان راکتیو سلف‌ها، هیچ کار واقعی انجام نمی‌دهد.

توان AC در یک مدار کاملا خازنی

یک مدار کاملا خازنی C برحسب فاراد (در این مدار اندوکتانس صفر  L=0 و رزیستانس بی نهایت  R=∞ است) دارای خاصیت تاخیر برای تغییرات ولتاژ  است. خازن‌ها انرژی الکتریکی را در قالب یک میدان الکتریکی با دی الکتریک،  ذخیره کرده و از اینرو، خازن خالص نه تنها هیچ انرژی تلف نمی‌کند؛ بلکه  ذخیره می‌نماید.

در یک مدار کاملا خازنی، ولتاژ نمی‌تواند همفاز با  جریان باشد و نیاز است؛ که صفحات خازن، ابتدا “شارژ شود”. این سبب می‌گردد  که شکل‌موج ولتاژ، به پیک یا مقدار حداکثر خود، زمانی بعد از جریان برسد.  نتیجه آن است که در یک مدار کاملا خازنی، جریان همواره “پیشرو” (ICE) از  ولتاژ با 90° (π/2)  اختلاف فاز است؛ که در زیر آمده است.

مدار کاملا خازنی

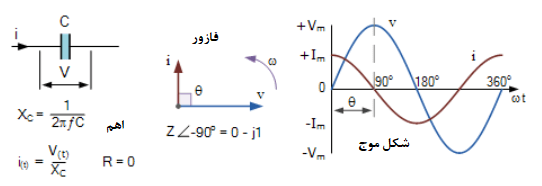
شکل موج‌های بالا، نشان می‌دهد که ولتاژ و جریان در یک خازن خالص، تابعی از زمان است. حداکثر جریان Im در ربع کامل یک سیکل (۹۰°) قبل از حداکثر (پیک) ولتاژ رخ می‌دهد. دربالا،  جریان با حداکثر مقدار مثبت خود، در ابتدا سیکل ولتاژ شروع کرده، از صفر  گذشته و به‌مقدار حداکثر منفی خود، زمانی‌که شکل‌موج ولتاژ در حداکثر خود  در ۹۰° قرار دارد می‌رسد. این شیفت فاز، معکوس مدار القایی خالص است.

بنابراین، در یک مدار کاملا خازنی، زاویه‌فاز θ=-۹۰° بوده و معادله‌ی توان متوسط راکتیو در خازن خواهد بود:

توان راکتیو در یک خازن خالص

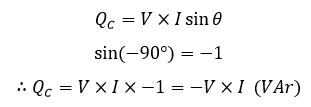
درجایی‌که: V*I*sin(θ)- یک موج‌سینوسی منفی است. همچنین نماد توان راکتیو خازنی QC با همان یکای اندازه‌گیری مشابه سلف، ولت-آمپر راکتیو (VAR) است. می‌توان  دید؛ که دقیقا مانند مدار کاملا القایی بالا، هیچ توان واقعی (P) را مصرف  یا اتلاف نمی‌کند.

شکل موج های توان AC برای یک خازن خالص

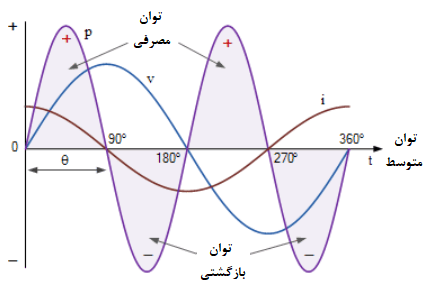
در نیمه مثبت شکل موج ولتاژ بین زاویه ۰° و ۰°۹، هر دو شکل  موج‌های جریان و ولتاژ مثبت بوده که نتیجه آن، توان مثبت مصرفی خواهد بود.  بین زاویه ۹۰° و ۰°۱۸، جریان خازن منفی بوده و ولتاژ منبع، هم‌چنان مثبت  است. از اینرو حاصل ولت-آمپر، توان منفی به‌ ما‌ می‌دهد؛ زیرا منفی در  مثبت، منفی خواهد شد. توان‌منفی، نشان‌دهنده‌ی این است که کویل انرژی  الکتریکی ذخیره شده را به منبع تغذیه بر می‌گرداند.

در نیمه منفی شکل  موج ولتاژ بین زاویه ۱۸۰° و ۲۷۰°، هر دو جریان خازن‌ها و ولتاژ منبع تغذیه  منفی بوده که نتیجه آن، توان مثبت در پریود است. این پریود توان مثبت،  نشان‌دهنده‌ی مصرف انرژی الکتریکی کویل از منبع‌تغذیه است. بین زاویه ۲۷۰° و  ۳۶۰°، ولتاژ منفی و جریان مثبت است که نشان‌دهنده‌ی توان منفی است.

پس  در طی یک سیکل کامل شکل موج ولتاژ، وضعیت مشابه مدار کاملا القایی وجود  دارد؛ دو پالس مثبت و منفی یکسان داریم که مقدار متوسط آن‌ها صفر است. از  این‌رو، توان داده شده از منبع به خازن دقیقا برابر با توان بازگشته به  منبع، توسط خازن است. درنتیجه، هیچ توان واقعی استفاده نمی‌شود، زیرا در  نهایت توان رفته و به منبع باز می‌گردد. این، به این‌معناست که کل توان  گرفته شده توسط خازن خالص طی یک سیکل، برابر با صفر است. بنابراین توان  راکتیو خازن‌‌ها، هیچ کار واقعی انجام نمی‌دهند.

مثال ۲

یک کویل سلونوئیدی، با رزیستانس (مقاومت)،30 اهم، اندوکتانس 200mH ، به منبع تغذیه 230VAC ,50Hz متصل است.

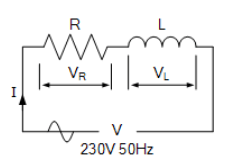
محاسبه‌ کنید:

1. امپدانس سلونوئید
2. جریان مصرفی توسط سلونوئید
3. زاویه فاز بین جریان و ولتاژ اعمالی
4. توان متوسط مصرف شده توسط سلونوئید.

داده‌های داده‌شده:

R = 30Ω, L = 200mH, V = 230V و ƒ = 50Hz

1. امپدانس (Z) یک کویل سلونوئیدی:

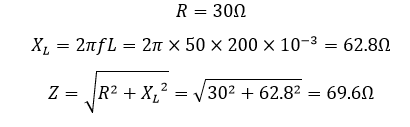
2. جریان مصرفی (I) توسط سلونوئید

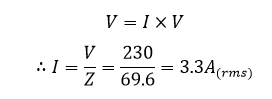
۳. زاویه فاز θ

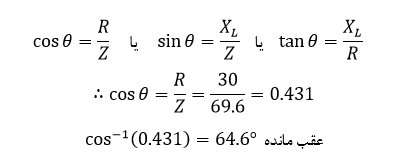
4. توان متوسط مصرف شده AC توسط سلونوئید

خلاصه توان الکتریکی AC

در اینجا دیدیم که در مدارهای AC، ولتاژ و جریان جاری در یک مدار  کاملا پسیو، معمولا خارج از فاز بوده و درنتیجه قادر به انجام کار واقعی  نیست. همچنین دیدیم که در یک مدار جریان مستقیم (DC)، توان الکتریکی برابر  با ضرب ولتاژ در جریان یا P=V*I است. اما، نمی‌توانیم آن‌ را به همان روش  که برای مدارهای AC در نظر گرفتیم، محاسبه‌کنیم.

در یک مدار مقاومتی  خالص، جریان و ولتاژ هر دو هم فاز می‌باشند و تمام توان الکتریکی توسط  مقاومت، معمولا به‌صورت گرما مصرف می‌شود. درنتیجه توان الکتریکی  به‌هیچ‌وجه به منبع‌تغذیه یا مدار باز نمی‌گردد.

اما، دریک مدار  کاملا القایی یا کاملا خازنی به‌دلیل حضور راکتانس (X)، جریان، پیشرو یا  عقب‌مانده از ولتاژ با زاویه‌ی دقیقا 90° (زاویه‌فاز) است. پس توان،  ذخیره‌شده و به منبع، باز می‌گردد. توان متوسط محاسبه‌شده، طی یک سیکل  پریودی کامل، برابر با صفر خواهد بود.

توان الکتریکی مصرفی توسط  رزیستانس (R) را، توان حقیقی یا واقعی می‌گویند و به سادگی با ضرب ولتاژ  rms در جریان rms به‌دست می‌آید. توان‌الکتریکی‌ ذخیره‌شده توسط راکتانس  (X) را، توان راکتیو می‌گویند و با ضرب ولتاژ، جریان و سینوس زاویه بین  آن‌ها به دست می‌آید.

نماد زاویه فاز، θ (تتا) بوده، و نشان‌دهنده‌ی  ناکارآمدی مدار AC نسبت به امپدانس کل راکتیو (Z) است که معکوس جریان جاری در مدار می‌باشد.