مثلث توان و ضریب توان

درآموزش مربوط به توان الکتریکی،  دیدیم که مدارهای AC دارای رزیستانس و ظرفیت خازنی یا رزیستانس و  اندوکتانس و یا هردو، دارای توان واقعی و توان راکتیو می‌باشند و برای  محاسبه کل توان مصرفی، نیاز به دانستن اختلاف فاز بین شکل موج‌های سینوسی  ولتاژ و جریان است.

در یک مدار AC، شکل موج های ولتاژ و جریان،  سینوسی بوده و بنابراین، دامنه های آن‌ها دائما با گذشت زمان تغییر می‌کند.  می‌دانیم که توان ضرب ولتاژ در جریان (P=V*I) است و حداکثر توان زمانی رخ  می‌دهد که دو شکل موج ولتاژ و جریان با‌هم، هم‌ردیف شوند. یعنی رسیدن به  پیک‌ها و صفرهای شکل موج‌ها، همزمان اتفاق بیفتد. به چنین اتفاقی، “هم فاز  بودن” دوشکل موج گفته می‌شود.

سه عنصر اصلی در مدار AC، که بر رابطه  بین شکل موج‌های ولتاژ و جریان و درنتیجه اختلاف فاز میان آن‌ها، اثرگذار  است؛ با تعریف امپدانس کل مدار، مقاومت، خازن و سلف است.

امپدانس (Z)  یک مدار AC، برابر با رزیستانس محاسبه‌شده در مدارهای DC است؛ که امپدانس  بر حسب اهم است. برای مدار های AC ، امپدانس در حالت کلی، به‌صورت نسبت  فازور ولتاژ و جریان تولید‌ شده توسط یکی از عناصر مدار، تعریف می‌گردد.  فازور ها، خطوط مستقیمی می‌باشند؛ که به‌گونه‌ای ترسیم می‌شوند که دامنه  ولتاژ و جریان را، توسط طول خود و تفاوت فاز، نسبت به خطوط فازور دیگر، با  موقعیت زاویه‌ای نسبت به فازوردیگر، نشان دهند.

مدارهای AC، شامل  رزیستانس و راکتانس بوده؛ که در ترکیب با یکدیگر، امپدانس کلی (Z) را تشکیل  می‌دهند؛ که سبب محدود شدن جریان جاری در مدار می‌شود. اما امپدانس در  مدارهای AC، برابر با مجموع مقادیر اهمی مقاومتی و راکتیوی نیست؛ زیرا  مقاومت خالص و راکتانس خالص، 90° با یک‌دیگر اختلاف فاز دارند. اما ما  می‌توانیم؛ از این اختلاف‌فاز 90°، برای اضلاع یک مثلث قائم‌الزاویه، به  نام مثلث امپدانس، استفاده کنیم. امپدانس در این مثلث، وتر است که توسط  قضیه فیثاغورث تعیین می‌شود.

 رابطه هندسی بین رزیستانس، راکتانس و امپدانس، را به‌صورت شکلی با استفاده از مثلث امپدانس می‌توان نشان داد.

مثلث امپدانس

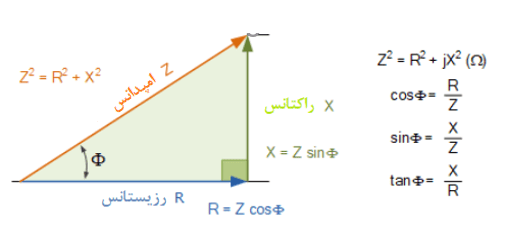
باید توجه داشت که امپدانس، که جمع برداری راکتانس و رزیستانس  است، نه تنها دارای اندازه (Z) بلکه دارای اختلاف‌فاز (φ) نیز می‌باشد؛ که  نشان دهنده‌ی اختلاف فاز بین رزیستانس و راکتانس است. همچنین توجه داشته  باشید، این مثلث به‌دلیل تغییرات در راکتانس (X) با تغییر فرکانس، تغییر  شکل می‌دهد. البته مقاومت (R) همیشه ثابت خواهد ماند.

می‌توانیم، با  تبدیل مثلث امپدانس به مثلث توان، که نمایانگر سه عنصر توان در یک مدار AC  است، این ایده را یک گام جلوتر ببریم. قانون اهم به ما می‌گوید که در مدار  DC، توان (P) برحسب وات، برابر با مربع جریان (I۲) ضرب در رزیستانس (R) است. بنابراین، می‌توانیم سه ضلع مثلث امپدانس بالا را، در I۲ ضرب کنیم تا مثلث توان متنظر را به‌دست آوریم:

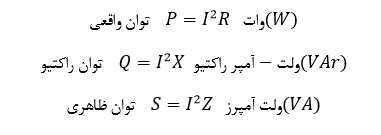
توان واقعی در مدار های AC

توان واقعی (P)،  که به عنوان توان حقیقی یا فعال نیز شناخته می‌شود، “کار واقعی” را در یک  مدار الکتریکی انجام می‌دهد. توان واقعی، برحسب وات، توان مصرف شده توسط  قسمت مقاومتی مدار است. توان واقعی (P) در مدار AC، همان توان P در مدار DC  است. از اینرو درمدارهای DC، توان با I۲*R، درجاییکه، R عنصر کل مقاومتی مدار است به دست می‌آید.

از  آن جایی که، رزیستانس‌ها، هیچ تفاوت فازوری (شیفت فاز) بین شکل موج‌های  ولتاژ و جریان ایجاد نمی‌کنند؛ تمام توان مفید، مستقیما به رزیستانس رسیده و  به گرما، نور و کار تبدیل می‌شود. پس توان مصرفی توسط یک مقاومت، توان  واقعی بوده که اساسا توان متوسط مدارها است.

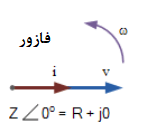
برای یافتن مقدار متناظر توان واقعی، مقادیر ولتاژ و جریان rms،  در کسینوس زاویه فاز (φ) ضرب می‌شود؛ همانطور که در زیر نشان داده شده‌است:

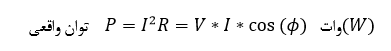
اما به دلیل این که، هیچ تفاوت فازی بین ولتاژ و جریان در یک مدار مقاومتی وجود ندارد؛ تغییر فاز بین دو شکل موج صفر خواهد بود. پس:

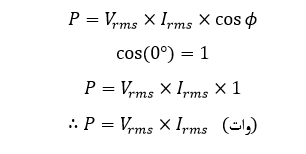
در اینجا توان واقعی (P) برحسب وات، ولتاژ (V) برحسب ولت rms و جریان (I) برحسب آمپر rms است.

توان واقعی I۲R  برای یک عنصر مقاومتی است، که برحسب وات اندازه‌گیری می‌شود. آن چیزی که  از روی کنتور انرژی خوانده می‌شود؛ دارای واحدهای وات (W)، کیلووات (KW) و  مگاوات (MW) است. توان واقعی P، همیشه مثبت است.

توان راکتیو در مدار های AC

توان راکتیو (Q)،  (گاهی آن را توان بدون وات نیز می‌نامند) توان مصرفی در یک مدار AC است که  کار مفیدی انجام نمی‌دهد اما تاثیر زیادی در تغییر فاز بین شکل موج ولتاژ و  جریان دارد. توان راکتیو، از راکتانس تولید‌ شده توسط سلف و خازن ناشی  می‌شود و اثرات توان واقعی را خنثی می‌کند. توان راکتیو در مدارهای DC،  وجود ندارد.

برخلاف توان واقعی (P)، که کار کل مدار را انجام می‌دهد،  توان راکتیو (Q) به‌دلیل ایجاد و نیز کاهش هر دو میدان مغناطیسی القایی و  میدان الکترواستاتیک خازنی، توان را از مدار می‌گیرد. بنابراین، انتقال  توان واقعی، که انتقال توان منبع به مدار یا بار است؛،دشوار خواهد شد.

توان  ذخیره‌شده توسط یک سلف در یک میدان مغناطیسی، سعی در کنترل جریان دارد.  درحالی‌که، توان ذخیره‌شده توسط میدان الکترواستاتیک خازن، سعی در کنترل  ولتاژ دارد. نتیجه این است که خازن‌ها توان راکتیو “تولید” و سلف‌ها توان  راکتیو “مصرف” می‌نمایند. این بدان معنی است که هردو انرژی مصرف کرده و به  منبع باز می‌گرداند و از این رو، هیچ توان واقعی مصرف نمی‌گردد.

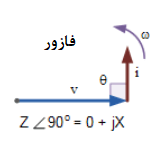
برای یافتن مقدار توان راکتیو، مقادیر ولتاژ و جریان rms، در سینوس زاویه‌فاز (φ) ضرب می‌شود. همانطور که در زیر نشان داده شده‌است:

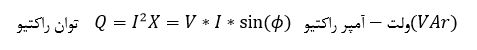
به دلیل 90° اختلاف فاز بین شکل موج‌های ولتاژ و جریان در یک  راکتانس خالص (چه القایی و چه خازنی) حاصل ضرب V*I*sin(φ)، برابر با جز  عمودی است که 90° با جز دیگر اختلاف فاز دارد، پس:

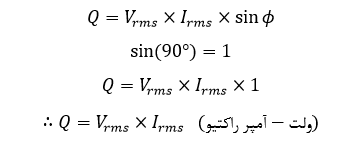
در جاییکه، توان راکتیو (Q) برحسب ولت آمپر راکتیو، ولتاژ (V)  برحسب ولت rms و جریان (I) برحسب آمپر rms است. توان راکتیو نشان دهنده‌ی  حاصل ولت و آمپر بوده که 90° اختلاف فاز دارند؛ اما در حالت کلی، امکان  وجود هر زاویه‌فاز (φ) بین ولتاژ و جریان وجود دارد.

توان راکتیو I۲X برای یک عنصر راکتیو، دارای واحدهای ولت آمپر راکتیو (VAr)، کیلو ولت آمپر راکتیو (KVAr) و مگا ولت آمپر راکتیو (MVAr) است.

توان ظاهری در مدار های AC

در بالا دیدیم که توان واقعی توسط مقاومت تلف می‌شود و توان  راکتیو به راکتانس داده می‌شود. پس شکل موج های ولتاژ و جریان همفاز نبوده؛  که دلیل آن، تفاوت بین عناصر مقاومتی و راکتیوی مدار است. رابطه‌ ریاضیاتی  بین توان واقعی (P) و توان راکتیو (Q)، توان مختلط خوانده می‌شود. حاصل  ضرب ولتاژ rms (V) اعمال‌شده به مدار AC و جریان rms (I) جاری در مدار  “محصول ولت-آمپر”(VA) خوانده می‌شود؛ که دارای نماد S بوده و اندازه آن  عموما، به‌عنوان توان ظاهری شناخته می‌شود.

توان مختلط، برابر با جمع  جبری توان های واقعی و راکتیو نیست؛ بلکه مجموع برداری P و Q بوده که  برحسب ولت آمپرز (VA) می‌باشد. توان مختلط با مثلث توان، نشان داده می‌شود.  مقدار rms حاصل ضرب ولت آمپر، معمولا به‌عنوان توان ظاهری شناخته می‌شود؛  زیرا “ظاهرا” این توان، کل توان مصرف شده توسط مدار است. حتی اگر توان  واقعی که کار انجام می‌دهد، بسیار کمتر باشد.

توان ظاهری، از دو بخش  تشکیل شده‌است؛ توان مقاومتی، که توان همفاز یا توان واقعی برحسب وات بوده و  توان راکتیو، که غیر همفاز و برحسب ولت آمپرز است. می‌توانیم جمع برداری  این دو جز توان را به‌شکل یک مثلث توان نشان دهیم. یک مثلث توان دارای 4 بخش P ،Q ،S و θ می‌باشد.

سه  عنصر تشکیل دهنده‌ی توان در مدار AC، را می‌توان به صورت گرافیکی، توسط سه  ضلع مثلث قائم الزاویه، تقریبا مشابه مثلث امپدانس قبلی نشان داد. ضلع  افقی (مجاور)، نشان‌دهنده‌ی توان واقعی (P) مدار، ضلع عمودی (مخالف) نشان  دهنده‌ی توان راکتیو (Q) مدار و وتر، نشان دهنده‌ی توان ظاهری (S) حاصل از  مثلث توان است که در زیر نشان داده‌ می‌شود.

مثلث توان یک مدار AC

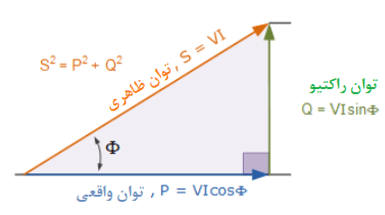
P: برابر با I۲*R یا توان واقعی است؛ که کار برحسب وات، W انجام می‌دهد.

Q: برابر با I۲*X یا توان راکتیو است؛ که برحسب ولت-آمپر راکتیو، VAr است.

S: برابر با I۲*Z یا توان ظاهری است؛ که برحسب ولت-آمپرز، VA است.

φ: زاویه فاز بر حسب درجه است. زاویه‌فاز بزرگتر، توان راکتیو بزرگتری دارد:

cos(φ) = P/S = W/VA = ضریب توان , p.f.

sin(φ) = Q/S = VAr/VA

tan(φ) = Q/P = VAr/W

ضریب توان، نسبت توان واقعی به توان ظاهری بوده؛ که برابر با cos(φ) است.

ضریب توان یک مدار AC

ضریب توان، cos(φ)، بخش مهمی از یک مدار AC است؛ که می‌تواند بر  حسب امپدانس مدار یا توان مدار نیز بیان شود. ضریب توان، به عنوان نسبت  توان واقعی (P) به توان ظاهری (Q) تعریف می‌شود و می‌تواند به صورت عدد  اعشاری به‌عنوان مثال 0.95 و یا به صورت درصد به‌عنوان مثال 95% باشد.

ضریب  توان، زاویه فاز بین شکل موج‌های جریان و ولتاژ، در جاییکه، I و V  اندازه‌های مقادیر rms جریان و ولتاژ است، می‌باشند. توجه داشته باشید که  فرقی ندارد که زاویه فاز، اختلاف جریان نسبت به ولتاژ بوده و یا اختلاف  ولتاژ نسبت به جریان؛ رابطه ریاضی آن به‌صورت زیر خواهد بود:

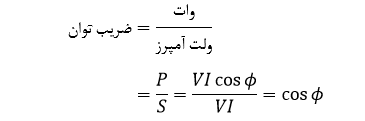
پیش از این گفتیم که در یک مدار کاملا مقاومتی، شکل موج‌های  جریان و ولتاژ، هم فاز با یکدیگر بوده و از این رو، توان مصرفی، همان توان  ظاهری به دلیل اختلاف فاز ۰ درجه (۰°) می‌باشد. پس ضریب توان خواهد بود:

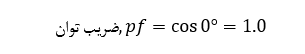
تعداد وات های مصرفی، برابر با تعداد ولت‌آمپر های مصرفی است که  ضریب توان ۱.۰ یا ۱۰۰% را تولید می‌کند. در این حالت ضریب توان واحد خواهیم  داشت.

همچنین، درمورد مدارهای کاملا راکتیوی گفتیم که شکل موج‌های  ولتاژ و جریان با یکدیگر ۹۰° اختلاف فاز دارند. از آن‌جایی که اختلاف فاز  برابر با نود درجه (۹۰°) است. ضریب توان خواهد بود:

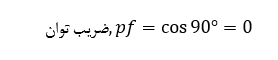
تعداد وات های مصرفی صفر بوده اما همچنان ولتاژ و جریانی وجود  دارد که بار راکتیو را تامین می‌کند. روشن است که کاهش جز راکتیو VAr مثلث  توان، سبب کاهش θ برای بهبود دادن ضریب توان به سمت 1 یا واحد است. همچنین  داشتن ضریب توان بالا نیز مطلوب است؛ زیرا مدار به‌صورت موثرتری جریان را  به بار تحویل می‌دهد.

پس می‌توانیم رابطه بین توان واقعی، توان ظاهری و ضریب توان مدار را به‌صورت زیر بنویسیم:

در یک مدار القایی که جریان از ولتاژ “عقب‌مانده” تر است (ELI)  ضریب توان عقب مانده بوده و در یک مدار خازنی که جریان “پیش‌رو” تر از  ولتاژ است (ICE) ضریب توان پیش‌رو می‌باشد.

مثال ۱

یک کویل حلقه‌ای ، دارای اندوکتانس 180mH  و رزیستانس 35Ω ، به منبع تغذیه 100VAC,50Hz متصل است.

 محاسبه‌ کنید:

۱. امپدانس کویل ۲. جریان ۳. ضریب توان ۴. توان ظاهری مصرف‌شده ۵. هم‌چنین مثلث توان حاصل را برای کویل فوق رسم کنید. داده‌ها:    

                           R = 35Ω, L = 180mH, V = 100V وƒ = 50Hz

1. امپدانس (Z) کویل

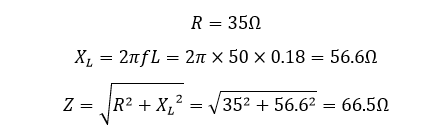
۲. جریان مصرفی (I) توسط کویل

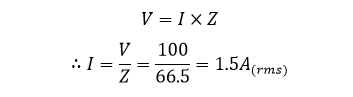
۳.  ضریب توان و زاویه‌فاز φ

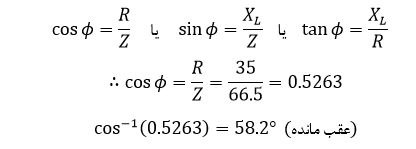
۴. توان ظاهری (S) مصرف شده توسط کویل

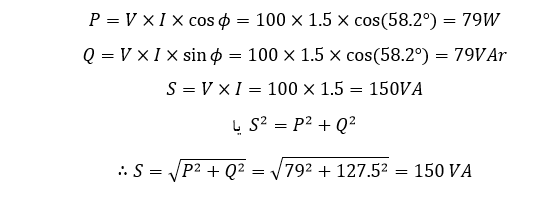
۵. مثلث توان برای کویل

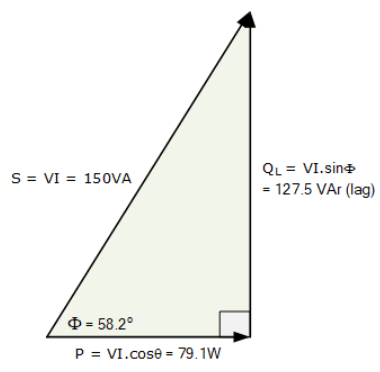
همانطور که روابط مثلث توان این مثال ساده نشان می‌دهد؛ برای  ضریب توان ۰.۵۲۶۳ یا ۵۲.۶۳%، کویل برای تولید ۷۹ وات کار مفید، به ۱۵۰ ولت  آمپر توان نیاز دارد. به بیان دیگر، برای ضریب توان ۵۲.۶۳%، کویل حدود ۸۹%  جریان بیشتری برای انجام همان کار می‌کشد که جریان تلف شده زیادی است.

افزودن  خازن تصحیح ضریب توان ( برای مثال 32.3uF) به کویل، برای افزایش ضریب توان  به 0.95 یا 95% ، توان راکتیو مصرفی توسط کویل را، به صورت چشم‌گیری کاهش  می‌دهد؛ زیرا این خازن‌ها، به‌صورت ژنراتور جریان راکتیو عمل کرده و  بنابراین، مقدار کل جریان مصرفی را کاهش می‌دهد.

خلاصه مثلث توان و ضریب توان

تا اینجا دیدیم؛ که سه جز یک توان الکتریکی: توان واقعی، توان راکتیو و توان ظاهری در یک مدار AC می‌توانند به صورت سه ضلع مثلث توان نشان داده شوند. به دلیل این که این سه جز، می‌توانند به‌صورت یک “مثلث  قائمه” نشان داده شوند، رابطه میان آن‌ها را می‌توان به صورت S۲ = P۲ + Q۲ تعریف نمود. در جایی که P، توان واقعی برحسب وات (W)، Q، توان راکتیو  برحسب ولت-آمپر راکتیو (VAr) و S توان ظاهری برحسب ولت-آمپرز (VA) است.

همچنین  در مدار AC دیدیم مقدار cos(φ) را ضریب توان می‌نامند. ضریب توان مدار AC،  با نسبت توان واقعی مصرفی (W) توسط مدار، به توان ظاهری (VA) مصرف شده  توسط همان مدار تعریف می‌شود. درنتیجه: توان ظاهری/توان واقعی=ضریب توان یا  p.f.=W/VA

کسینوس زاویه حاصل بین ولتاژ و جریان برابر با ضریب توان  خواهد بود. در حالت کلی، ضریب توان می‌تواند با درصد مانند 95% یا عدد  اعشاری مانند 0.95 بیان شود. زمانیکه، ضریب توان برابر با 1 (واحد) یا   100% است؛ توان واقعی مصرفی، برابر با توان ظاهری مدار و زاویه فاز بین  جریان و ولتاژ 0° بوده و cos-۱(1.0)=0° است. زمانی که، ضریب توان برابر با صفر (0) است زاویه فاز بین جریان و ولتاژ 90° بوده و cos-۱(0)=90° است. در این صورت، توان واقعی مصرفی توسط مدار AC، بدون توجه به جریان مدار، صفر است.

در  مدار های عملی AC، ضریب توان می‌تواند جایی بین 0 تا 1، وابسته به عناصر  پسیو متصل به بار باشد. برای یک بار القایی- مقاومتی یا مدار (که معمولا  چنین است) ضریب توان، “عقب‌مانده” خواهد بود. در یک مدار خازنی-مقاومتی،  ضریب توان “پیشرو” می‌باشد. پس یک مدار AC می‌تواند شامل ضریب ‌توان واحد،  عقب‌مانده یا پیشرو باشد.

ضریب توان کم با مقداری نزدیک به صفر (۰)،  توان تلف شده را مصرف نموده و سبب کاهش کارایی مدار می‌شود؛ در‌ حالی که،  مدار یا بار با ضریب‌توان نزدیک به ۱ یا واحد (%۱۰۰) بسیار کارآمد تر خواهد  بود و دلیل آن این است که یک مدار یا بار، با ضریب توان کمتر، نیاز به  جریان بیشتری برای همان مدار یا بار نسبت به ضریب توان نزدیک به ۱ (واحد)  دارد.