مدار شارژ کننده RC

زمانی‌که، یک منبع ولتاژ به یک مدار RC اعمال می‌شود؛ خازن C از طریق مقاومت R شارژ می‌شود.

تمام مدارهای الکتریکی یا الکترونیکی، با شکلی از “تاخیر زمانی” بین پایانه‌های ورودی و خروجی خود درگیر می‌باشند. این اتفاق به نوع سیگنال یا ولتاژ اعمالی به مدار، چه مستقیم (DC) باشد و چه متناوب (AC) وابسته نیست.

این تاخیر، معمولا با نام تاخیر زمانی یا ثابت زمانی مدار شناخته می‌شود و نشان‌دهنده‌ی پاسخ زمانی، در هنگام اعمال ورودی پله‌ی سیگنال یا ولتاژ به مدار است. ثابت زمانی برآیند هر مدار یا سیستم الکترونیکی، عمدتا به قطعات خازنی یا القایی که به مدار متصل شده‌است؛ وابسته می‌باشد. این ثابت زمانی، دارای یکای تاو یا τ می‌باشد.

زمانی‌که، یک ولتاژ DC درحال افزایش به یک خازن خالی از شارژ اعمال می‌شود؛ خازن، چیزی که نام “جریان شارژ” دارد؛ را می‌کشد و “شارژ می‌شود”. زمانی که ولتاژ کاهش یافت؛ خازن شروع به خالی‌شدن در جهت مخالف می‌نماید. به همین دلیل که خازن‌ها می‌توانند انرژی الکتریکی را ذخیره کنند؛ می‌توانند در بسیاری از موارد مانند باتری‌های کوچک، انرژی را در صورت نیاز در صفحات خود ذخیره کرده و آزاد کنند.

شارژ الکتریکی ذخیره‌شده برروی صفحات یک خازن به‌صورت Q=CV بیان می‌شود . این شارژشدن (ذخیره‌کردن) یا خالی‌شدن شارژ (آزادسازی) انرژی خازن‌ها، هیچ‌گاه لحظه‌ای نیست و مقدار زمان مشخصی طول می‌کشد تا رخ دهد و از این‌رو، به زمان گرفته شده توسط خازن برای شارژ یا خالی‌شدن، که مرتبط با درصد مشخصی از مقدار حداکثر ولتاژ منبع است؛ ثابت زمانی (τ) گفته می‌شود.

اگر یک خازن در حالت سری با خازن، یک مدار RC را شکل دهد؛ خازن تدریجا از طریق مقاومت تا زمانی که ولتاژ دوسر آن به مقدار منبع ولتاژ برسد؛ شارژ می‌شود. زمان موردنیاز برای خازن، تا بتواند کاملا شارژ شود؛ تقریبا معادل با ۵ ثابت زمانی یا 5τ است. پس، پاسخ گذرای یک مدار سری RC برابر با 5 ثابت زمانی است.

پاسخ زمانی گذرای T، به‌صورت T = RC و برحسب ثانیه محاسبه می‌شود. در این معادله؛ R ارزش مقاومت برحسب اهم و C ارزش خازن برحسب فاراد است. درنتیجه، برحسب این تفکر، پایه‌ی مدار شارژ کننده‌ی RC از طریق 5T برابر با “RC*5” شکل می‌گیرد.

مدار شارژ کننده‌ی RC

شکل زیر، یک خازن (C) سری‌شده با مقاومت (R)را در یک مدار شارژکننده‌ی RC نشان می‌دهد؛ که به یک منبع باتری DC (VS) به همراه یک کلید مکانیکی اتصال دارد. در زمان صفر و در هنگامی که کلید برای بار اول بسته می‌شود؛ خازن تدریجا شروع به شارژشدن از طریق خازن می‌نماید تا ولتاژ دو سر آن به ولتاژ منبع باتری برسد. این رفتار، که شارژشدن خازن است، در زیر نشان داده شده‌است.

شماتیک مدار شارژ کننده‌ RC

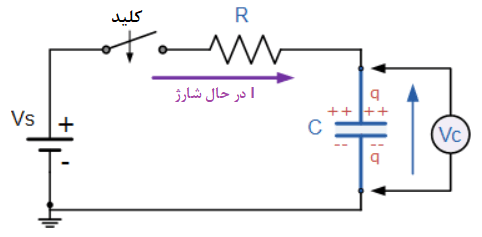
اجازه بدهید برای مدار بالا، فرض کنیم؛ که خازن،C کاملا خالی از شارژ و کلید (S) کاملا باز است. این موارد، شرایط اولیه‌ی مدار یعنی، t=0، i=0 و q=0 است. زمانی‌که، کلید بسته شده، زمان از t=0 شروع کرده و جریان شروع به شارژ خازن از طریق مقاومت می‌نماید.

از آنجایی‌که ولتاژ اولیه دوسر خازن در زمان صفر (t=0) برابر با صفر است (VC=0)؛ خازن نسبت به یک مدار خارجی درحالت اتصال کوتاه بوده و به نظر میرسد؛ که حداکثر جریان عبوری از مدار فقط توسط مقاومت R محدود شده‌است. پس با استفاده از قانون ولتاژ کیرشهف (KVL)، افت ولتاژ دو سر مدار به‌صورت زیر خواهدبود:

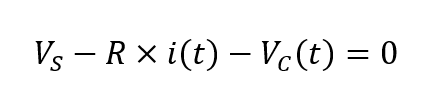
جریانی که در مدار شارش دارد؛ دراینجا جریان شارژشدن، نامیده می‌شود و برحسب قانون اهم به‌صورت i=Vs/R بیان می‌شود.

منحنی‌های مدار شارژ کننده‌ RC

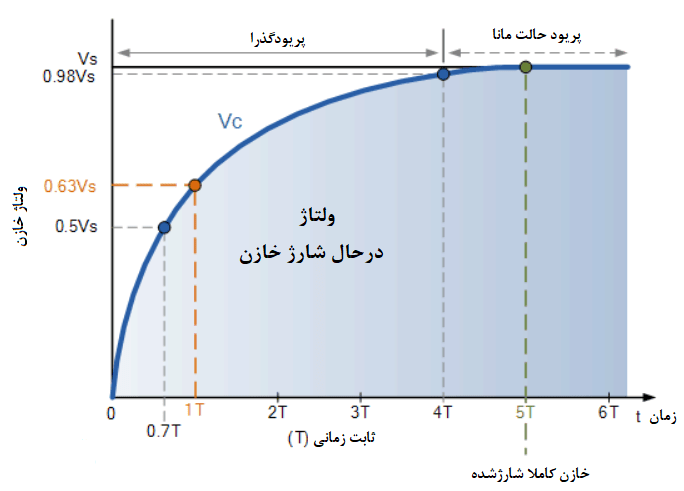
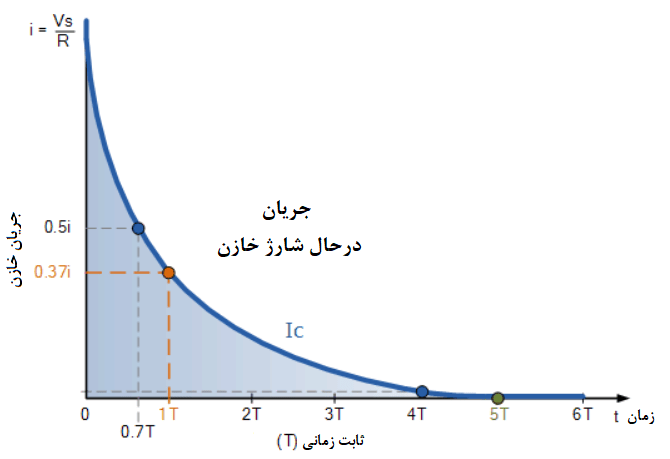
خازن (C) برحسب نرخی که در نمودار بالا نشان داده شده‌است؛ شارژ می‌شود. افزایش شیب منحنی شارژکننده‌ی RC در ابتدا بسیار تندتر است؛ زیرا سرعت شارژ در شروع شارژشدن، سریع‌ترین حالت است؛ اما بعد از مدت زمان کوتاهی به‌صورت نمایی کاهش می‌یابد؛ زیرا خازن شارژ اضافی را با سرعت کمتری دریافت می‌کند.

درحالی‌که خازن در حال شارژشدن است؛ اختلاف پتانسیل در دو سر صفحات خازن شروع به افزایش یافتن نسبت زمان واقعی که برای شارژ خازن نیاز است؛ می‌نماید تا به 63% از حداکثر مقدار شارژ کامل ممکن برسد که در نمودار ما برابر با 0.63VS  و در یک ثابت زمانی کامل (T) رخ می‌دهد.

به این نقطه‌ی 0.63VS  به‌صورت مخفف 1T ( یک ثابت زمانی) داده می‌شود.

شارژشدن خازن ادامه می‌یابد و اختلاف ولتاژ بین دو مقدار VS و VC به‌همراه جریان مدار،i کاهش می‌یابد. درنتیجه، شرط نهایی که بزرگتر از 5 ثابت زمانی (5τ)، درهنگامی‌که خازن کاملا شارژ شده است؛ می‌باشد، برابر با t=∞، i=0 و q=Q=CV است. در بی‌نهایت، جریان شارژشدن، نهایتا به صفر می‌رشد و خازن مانند مدار باز عمل می‌کند و در این حالت، ولتاژ منبع تغذیه کاملا به دوسر خازن یعنی VS = VC منتقل شده‌است.

پس از نظر ریاضیاتی، می‌تواننیم بگوییم که زمان لازم برای شارژشدن خازن در یک ثابت زمانی (1T) به‌‌صورت زیر است:

ثابت زمانی RC، تاو

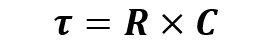
این ثابت زمانی RC فقط نرخ شارژ را مشخص می‌کند؛ که در این معادله R برحسب Ω و C برحسب فاراد است.

از آنجایی‌که ولتاژ V که مرتبط با شارژ خازن است؛ با معادله‌ی VC=Q/C مشخص می‌شود. ولتاژ دوسر خازن (VC) را در هر لحظه‌ای از زمان، در بازه‌ی زمانی شارژشدن، می‌توان به‌صورت زیر بیان کرد:

در این فرمول:

VC ، ولتاژ دو سر خازن است.

VS ، ولتاژ منبع تغذیه است.

e ، یک عدد غیرمنطقی است؛ که توسط اویلر برابر با 2.7182 ارائه شده‌است.

t ، زمان سپری‌شده از اعمال ولتاژ منبع تغذیه است.

RC ، ثابت زمانی مدار شارژشدن RC است.

پس از یک دوره‌ی زمانی معادل با 4 ثابت زمانی (4T)، خازن این مدار شارژ RC تقریبا، کاملا شارژ می‌شود؛ زیرا ولتاژ ایجادشده در صفحات خازن، به 98% از حداکثر مقدار خود یعنی 0.98VS رسیده‌است. دوره‌ی زمانی لازم برای رسیدن خازن به این نقطه‌ی 4T به‌عنوان دوره‌ی گذرا شناخته می‌شود.

بعد از زمان 5T، خازن کاملا شارژ شده و ولتاژ دو سر خازن(VC) تقریبا برابر با ولتاژ منبع تغذیه (VS) است. از آنجایی‌که، خازن کاملا شارژ شده‌است؛ هیچ جریان دیگری در مدار شارش نمی‌یابد (IC=0). پریود زمانی پس از پریود زمانی 5T معمولا با نام پریود حالت مانا، شناخته می‌شود.

پس می‌توانیم؛ در جدول زیر مقادیر درصدی ولتاژ و جریان را برای خازن در مدار شارژی RC و برای ثابت زمانی معین، نشان دهیم.

جدول شارژ RC

باید توجه داشت؛ که منحنی شارژ برای یک مدار شارژکننده‌ی RC نمایی بوده و خطی نیست. این امر دارای این معنی است؛ که در واقعیت خازن هرگز به 100% شارژ کامل نمی‌رسد. بنابراین، برای تمام اهداف عملی، خازن پس از پنج ثابت زمانی (5T) به 99.3% شارژ می‌رسد و به همین دلیل، در این مرحله کاملا شارژشده در نظرگرفته می‌شود.

از آنجایی‌که، ولتاژ دو سر خازن VC  با زمان تغییر می‌کند و بنابراین، در هر ثابت زمانی تا 5T مقدار متفاوتی است و می‌توانیم مقدار ولتاژ خازن، VC را در هر نقطه‌ی مشخصی محاسبه کنیم. برای مثال:

مثال شماره‌ی 1 مدار شارژکننده‌ی RC

ثابت زمانی، T مدار RC را در مدار زیر بیابید.

ثابت زمانی، T با استفاده از فرمول T= R x C برحسب ثانیه به‌دست می‌آید.

از این‌رو، ثابت زمانی، T به‌صورت  می‌آید.

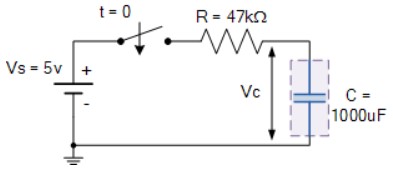
از این‌رو، ثابت زمانی، T به‌صورت زیر بدست می‌آید :

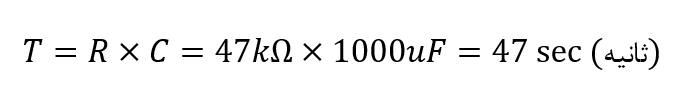
1. مقدار ولتاژ دو صفحه خازن در ۰.۷ ثابت زمانی چقدر است؟

در 0.7 ثابت زمانی (0.7T)، VC = 0.5 VS است و درنتیجه:

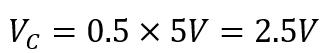
۲. مقدار ولتاژ دو صفحه خازن در ۱ ثابت زمانی چقدر است؟

در 1 ثابت زمانی(1T)، VC = 0.63 VS است و درنتیجه :

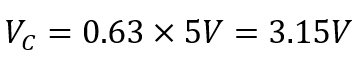
۳. چقدر طول می‌کشد؛ تا خازن، “شارژ کامل” را از منبع تغذیه بگیرد؟

از قبل آموختیم؛ که خازن پس از 5 ثابت زمانی (5T) به‌طور کامل شارژ می‌شود.

1 ثابت زمانی (1T) = 47 ثانیه( از جدول بالا) و از این‌رو،  5T=5 x 47=235ثانیه است.

۴. ولتاژ دو سر خازن بعد از ۱۰۰ ثانیه چقدر است؟

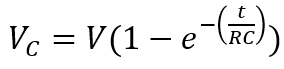
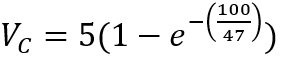
در این فرمول، ولتاژ برابر با 5 ولت (V = 5volt)، زمان برابر با 100 ثانیه (t =100 seconds) و RC برابر با 47 ثانیه (RC= 47 seconds) است.

از این رو:

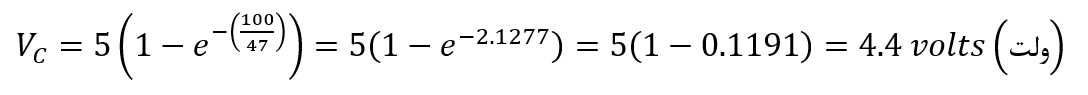
ما در این آموزش دیدیم؛ که شارژ یک خازن با عبارت Q=CV بیان می‌شود؛ که در آن، C مقدار ثابت خازن است و V ولتاژ اعمال شده‌است. همچنین آموختیم؛ که وقتی ولتاژی، در ابتدا به صفحات خازن اعمال می‌شود؛ با نرخی که توسط ثابت زمانی RC آن تعیین می‌شود؛ شارژ می‌شود و پس از پنج ثابت زمانی یا 5T، شارژ کامل برای آن درنظر گرفته می‌شود.

در آموزش بعدی رابطه‌ی بین جریان-ولتاژ یک خازن تخلیه‌ی شارژ را بررسی می‌کنیم و منحنی‌های تخلیه‌ی شارژ مرتبط به آن را، در زمانی که صفحات خازن به‌طور موثری به‌هم متصل می‌باشند؛ نگاه خواهیم کرد.