انتگرال گیر RC

انتگرال‌گیر RC، یک شبکه‌ی اتصال سری RC است؛ که سیگنال خروجی را مطابق با فرآیند ریاضی انتگرال‌گیری تولید می‌کند.

انتگرال‌گیر RC

برای یک مدار انتگرال‌گیر RC، سیگنال ورودی به مقاومت اعمال می‌شود و خروجی از دو سر خازن گرفته می‌شود و یعنی VOUT برابر با VC است. از آنجایی‌که، خازن یک قطعه‌ی وابسته به فرکانس است؛ مقدار باری که دو سر صفحات ایجاد می‌شود؛ برابر با انتگرال حوزه‌ی زمان از جریان است. یعنی زمان مشخصی طول می‌کشد؛ تا خازن به‌طور کامل شارژ شود؛ زیرا خازن نمی‌تواند آنی شارژ شود و فقط به‌صورت نمایی، این اتفاق می‌افتد.

بنابراین، جریان خازن را می‌توان به‌صورت زیر نوشت:

این معادله‌ی پایه‌ای بالا iC=C(dVC/dt) ، می‌تواند به‌عنوان نرخ لحظه‌ای تغییر شارژ نیز، بیان شود. Q باتوجه به زمان معادله‌ی استاندارد iC=(dQ/dt) بدست می‌آید؛ که شارژ برابر با ضرب ظرفیت خازنی در ولتاژ، Q=C x VC است.

سرعت شارژشدن (یا تخلیه‌ی شارژ) خازن با مقدار مقاومت و خازن، که ثابت زمانی را به ما می‌دهد؛ نسبت مستقیم دارد. بنابراین، ثابت زمانی یک مدار انتگرال‌گیر RC، بازه‌ی زمانی برابر با حاصل‌ضرب R و C است.

 ظرفیت خازن برابر با Q/VC است و در این معادله Q برابر با شارش جریان (i) در طول زمان (t) است. به این معنا که Q حاصل‌ضرب i x t برحسب کولمب است و از قانون اهم نیز می‌دانیم؛ که ولتاژ (V) برابر با i x R است. با جایگذاری این موارد در معادله‌ی ثابت زمانی RC خواهیم داشت:

ثابت زمانی RC

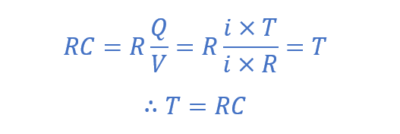
در معادله‌ی بالا، i و R خنثی می‌شوند و فقط T باقی می‌ماند؛ که نشان می‌دهد ثابت زمانی مدار انتگرال‌گیر RC، دارای بعد زمان برحسب ثانیه است و حرف یونانی تاو،T به آن داده شده‌است. توجه داشته‌باشید؛ که این ثابت زمانی، نشان‌دهنده‌ی زمان ( برحسب ثانیه) موردنیاز خازن برای شارژشدن تا 63.2% حداکثر ولتاژ یا تخلیه‌شدن تا 36.8% حداکثر ولتاژ است.

ولتاژ خازن

پیش از این گفتیم؛ که برای انتگرال‌گیر RC، خروجی برابر با ولتاژ دوسر خازن بوده و یعنی VOUT برابر با VC است. این ولتاژ متناسب با شارژ،Q ذخیره‌شده در خازن است و بار برابر با Q= V x C است.

نتیجه این است؛ که ولتاژ خروجی، انتگرال ولتاژ ورودی است و مقدار انتگرال وابسته به مقادیر R و C و درنتیجه ثابت زمانی شبکه است.

در بالا دیدیم؛ که جریان خازن را می‌توان به‌صورت نرخ تغییر بار Q نسبت به زمان بیان کرد. بنابراین، با استفاده از یک قانون اساسی حساب دیفرانسیل، مشتق Q نسبت به زمان، dQ/dt است و چون i= dQ/dt است؛ می‌توانیم، رابطه زیر را بدست آوریم:

از آنجایی‌که، ورودی به مقاومت متصل است؛ یک جریان،i هم از مقاومت و هم از خازن می‌گذرد (iR=iC) و سبب افت ولتاژ VR دوسر مقاومت می‌شود. پس جریان (i)، جاری در این شبکه‌ی RC به‌صورت زیر خواهدبود:

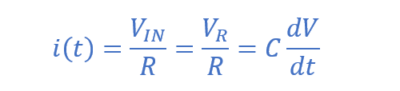
بنابراین:

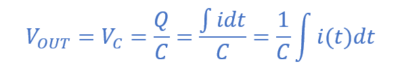
از آنجایی‌که i=VIN/R است؛ جایگذاری و تنظیم مجدد برای VOUT، به‌عنوان تابعی از زمان به ما خواهد داد:

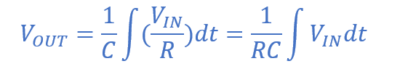
بنابراین، به‌ عبارت دیگر، خروجی مدار انتگرال‌گیر RC که ولتاژ دو سر خازن است؛ برابر با انتگرال زمانی ولتاژ ورودی،VIN است؛ که دارای وزن ثابت 1/RC است و RC نشان‌دهنده‌ی ثابت زمانی،T است.

پس با فرض صفربودن شارژ اولیه‌ی خازن، یعنی VOUT=0 و ثابت‌بودن ولتاژ ورودی VIN، ولتاژ خروجی،VOUT در حوزه‌ی زمان، به‌صورت زیر بیان می‌شود:

فرمول انتگرال‌گیر RC

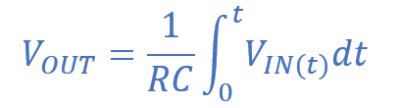
بنابراین، یک مدار انتگرال‌گیر RC مداری است؛ که در آن ولتاژ خروجی، VOUT متناسب با انتگرال ورودی است و با در نظرگرفتن این موضوع، اگر یک تک پالس مثبت را به شکل ولتاژ پله به مدار انتگرال‌گیر RC وارد کنیم؛ چه خواهد شد؟!

تک پالس انتگرال‌گیر RC

هنگامی‌که، یک پالس ولتاژ یک پله‌ای، به ورودی یک انتگرال‌گیر RC اعمال می‌شود؛ خازن، در پاسخ به پالس از طریق مقاومت، شارژ می‌شود. با این‌حال، خروجی آنی نیست؛ زیرا ولتاژ در خازن نمی‌تواند به‌طور لحظه‌ای تغییر کند و به‌صورت نمایی افزایش می‌یابد. زیرا خازن با نرخی که توسط ثابت زمانی RC،T=RC  تعیین می‌شود؛ شارژ می‌شود.

کنون می‌دانیم؛ که نرخ شارژ یا تخلیه‌ی شارژ خازن با ثابت زمانی RC مدار تعیین می‌شود. اگر یک پالس ولتاژ پله‌ی ایده‌آل، اعمال شود؛ یعنی با درنظرگرفتن لبه‌ی جلو و لبه‌ی دنباله، ولتاژ در خازن به‌صورت نمایی در زمان برای شارژشدن افزایش و برای تخلیه، کاهش می‌یابد و نرخ آن به‌صورت زیر تعیین می‌شود:

شارژ شدن خازن

تخلیه شارژ خازن

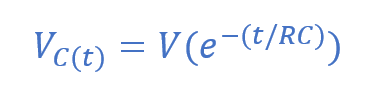
بنابراین، اگر ولتاژ خازن را یک ولت (1V) فرض کنیم؛ می‌توانیم درصد شارژشدن یا تخلیه‌ی شارژ خازن را برای هر ثابت زمانی R مجزا، مطابق جدول زیر رسم کنیم.

توجه داشته باشید؛ که در ۵ ثابت زمانی یا بالاتر، خازن ۱۰۰% شارژ کامل یا تخلیه‌ی شارژ کامل در نظر گرفته می‌شود.

بنابراین، اکنون فرض می‌کنیم، یک مدار انتگرال‌گیر RC متشکل از یک مقاومت 100kΩ و یک خازن 1uF همانطور که نشان داده شده‌است؛ داریم:

مثال مدار انتگرال‌گیر RC

ثابت زمانی،T یک مدار انتگرال‌گیر RC به‌صورت RC=100kΩ x 1uF=100ms بدست می‌آید.

بنابراین، اگر یک پالس ولتاژ پله‌ای را به ورودی با دوره‌ی مثلا ۲ ثابت زمانی (۲۰۰ میلی‌ثانیه) اعمال کنیم؛ از جدول بالا، می‌بینیم که خازن تا ۸۶.۴% از مقدار شارژ کامل خود، شارژ می‌شود. اگر این پالس، دارای دامنه‌ی ۱۰ ولت باشد؛ آنگاه این مقدار برابر با ۸.۶۴ ولت است؛ قبل از اینکه خازن دوباره از طریق مقاومت به منبع تخلیه شود و پالس ورودی به صفر برسد.

اگر فرض کنیم، که خازن مجاز است در زمان ۵ ثابت زمانی یا ۵۰۰ میلی ثانیه قبل از رسیدن پالس ورودی بعدی، به‌طور کامل تخلیه شود؛ نمودار منحنی‌های شارژ و تخلیه شارژ چیزی شبیه به زیر خواهدبود:

منحنی‌های شارژ / دشارژ انتگرال‌گیر RC

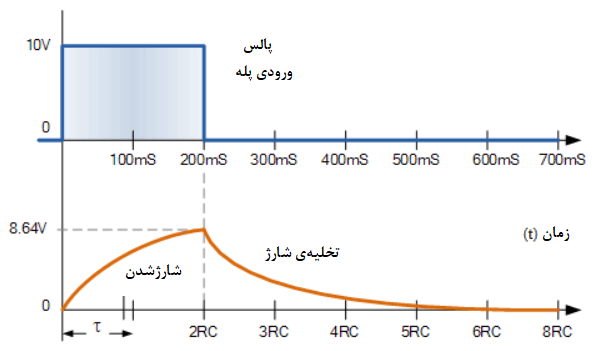
باید توجه داشت؛ که خازن از مقدار اولیه‌ی ۸.۶۴ ولت(۲ برابر ثابت زمانی) تخلیه می‌شود و نه از ۱۰ ولت ورودی.

پس می‌توانیم ببینیم؛ که با ثابت‌بودن ثابت زمانی RC، هرگونه تغییر در عرض پالس ورودی بر خروجی مدار انتگرال‌گیر RC تاثیر می‌گذارد. اگر عرض پالس افزایش یابد و یا برابر یا بزرگتر از 5RC باشد؛ شکل پالس خروجی، مشابه شکل ورودی خواهدبود؛ زیرا ولتاژ خروجی به همان مقدار ورودی می‌رسد.

با این‌حال، اگر عرض پالس به زیر 5RC کاهش یابد؛ خازن فقط تا حدی شارژ می‌شود و به حداکثر ولتاژ ورودی نمی‌رسد ودرنتیجه، ولتاژ خروجی کمتر می‌شود؛ زیرا خازن نمی‌تواند به‌اندازه کافی شارژ شود و درنتیجه، ولتاژ خروجی متناسب با انتگرال ولتاژ ورودی می‌شود.

پس، اگر یک پالس ورودی را برابر با یک ثابت زمانی یعنی 1RC،  فرض کنیم؛ خازن نه بین 0 و 10 ولت بلکه بین 63.2% و 38.7% ولتاژ دوسر خازن، در زمان تغییر شارژ و تخلیه می‌شود. توجه داشته باشید؛ این مقادیر با ثابت زمانی  RC تعیین می‌شوند.

ثابت زمانی انتگرال‌گیر RC ثابت

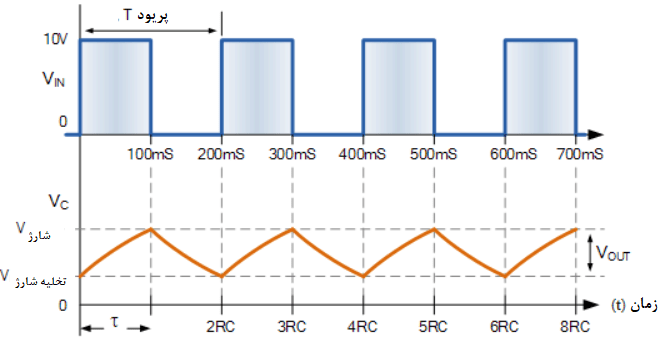
بنابراین، برای یک ورودی پالس پیوسته، رابطه صحیح بین زمان پریودیک ورودی و ثابت زمانی RC مدار، انتگرال ورودی است و نوعی رمپ بالا و سپس رمپ پایین برای خروجی، ایجاد می‌کند. اما برای اینکه مدار به‌درستی عمل کند؛ مقدار ثابت زمانی RC باید در مقایسه با زمان تناوبی ورودی‌ها بزرگ باشد. یعنی ، باشد و معمولا 10 برابر بزرگتر است.

این بدان معنی است؛ که بزرگی ولتاژ خروجی (که متناسب با 1/RC است) بین ولتاژهای بالا و پایین آن، بسیار کوچک بوده و به شدت ولتاژ خروجی را کاهش می‌دهد. این امر، به این دلیل است؛ که خازن، زمان بسیار کمتری برای شارژشدن و تخلیه‌ی شارژ بین پالس‌ها دارد اما متوسط ولتاژ DC خروجی، نصف مقدار ورودی افزایش می‌یابد و در مثال پالس ما در بالا، 5 ولت (10/2) خواهدبود.

انتگرال‌گیر RC به‌عنوان یک ژنراتور موج سینوسی

در بالا دیدیم؛ که یک مدار انتگرال‌گیر RC می‌تواند، عملیات انتگرال‌گیری را با اعمال یک ورودی پالس انجام دهد؛ که منجر به خروجی موج مثلثی رمپ بالا و رمپ پایین، به‌دلیل مشخصه‌های شارژ و تخلیه شارژ خازن می‌شود. اما اگر فرآیند را معکوس کنیم و شکل‌موج مثلثی را به ورودی اعمال کنیم؛ چه اتفاقی می‌افتد؟آیا یک خروجی پالس یا موج مربعی، دریافت می‌کنیم؟

هنگامی‌که سیگنال ورودی به مدار انتگرال‌گیر RC ،یک ورودی پالسی‌شکل باشد؛ خروجی یک موج مثلثی است. اما وقتی یک موج مثلثی اعمال می‌کنیم؛ به‌دلیل انتگرال سیگنال رمپ در زمان، خروجی به یک موج سینوسی، تبدیل می‌شود.

راه‌های زیادی برای تولید شکل‌موج سینوسی وجود دارد؛ اما یک راه ساده و ارزان برای تولید الکترونیکی شکل‌موج‌های سینوسی، استفاده از یک جفت مدار انتگرال‌گیر پسیو RC است؛ که به‌صورت موازی به‌هم متصل شده‌اند.

انتگرال‌گیر RC موج سینوسی

در اینجا، اولین انتگرال‌گیر RC، ورودی پالسی‌شکل اصلی را به شکل‌موج مثلثی رمپ بالا و رمپ پایین تبدیل می‌کند؛ که به ورودی انتگرال‌گیر دوم RC تبدیل می‌شود. این مدار انتگرال‌گیر دوم RC، نقاط شکل‌موج مثلثی را گرد کرده و آن را موج سینوسی تبدیل می‌کند؛ زیرا به‌طور موثر، یک انتگرال‌ دوگانه روی سیگنال ورودی اصلی انجام می‌دهد و ثابت زمانی RC بر درجه‌ی انتگرال، تاثیر می‌گذارد.

از آنجایی‌که انتگرال یک رمپ، یک تابع سینوسی تولید می‌کند (در اصل، یک شکل‌موج مثلثی گردشده) فرکانس پریودیک آن برحسب هرتز برابر با دوره‌ی T پالس اصلی خواهدبود. همچنین توجه داشته باشید؛ که اگر سیگنال را معکوس کنیم و سیگنال ورودی یک موج سینوسی باشد؛ مدار به‌عنوان انتگرال‌گیر عمل نمی‌کند؛ بلکه به‌عنوان یک فیلتر پایین‌گذر ساده (LPF) با موج سینوسی، عمل کرده که شکل‌موج خالص را تغییر نمی‌دهد؛ بلکه دامنه آن را تحت تاثیر قرار می‌دهد.

خلاصه‌ی انتگرال‌گیر RC

دراین مقاله دیدیم؛ که انتگرال‌گیر RC اساسا یک مدار فیلتر پایین‌گذر سری RC است؛ که وقتی یک پالس ولتاژ پله‌ای به ورودی آن اعمال می‌شود؛ خروجی متناسب با انتگرال ورودی آن را تولید می‌کند. این امر، یک معادله‌ی استاندارد  را تولید می‌کند؛ که در آن Vi سیگنالی است؛ که به انتگرال‌گیر داده می‌شود و Vo سیگنال خروجی انتگرال‌گیری شده‌است.

انتگرال‌گیری تابع پله‌ی ورودی، یک خروجی شبیه یک تابع رمپ مثلثی با دامنه‌ای کوچکتر از ورودی پالس اصلی، به‌همراه مقدار میرایی که توسط ثابت زمانی تعیین می‌شود؛ ایجاد می‌کند. بنابراین، شکل‌موج خروجی به رابطه‌ی بین ثابت زمانی مدار و فرکانس(دوره) پالس ورودی، بستگی دارد.

ثابت زمانی انتگرال‌گیرهای RC، همیشه با دوره‌ی T ورودی، مقایسه می‌شود. بنابراین، یک ثابت زمانی بزرگ RC، یک شکل‌موج مثلثی با دامنه‌ی کم، در مقایسه با سیگنال ورودی ایجاد می‌کند؛ زیرا خازن زمان کمتری برای شارژ یا تخلیه‌ی شارژ کامل دارد. ثابت زمانی کوچک، به خازن زمان بیشتری برای شارژ و تخلیه می‌دهد و شکل گرد معمولی‌تری ایجاد می‌کند.

اتصال دو مدار انتگرال‌گیر RC به‌صورت موازی، اثر انتگرال‌گیری دوگانه بر روی پالس ورودی دارد. نتیجه‌ی این انتگرال‌گیری دوگانه، این است؛ که مدار انتگرال‌گیر اول، پالس ولتاژ پله‌ای را به شکل‌موج مثلثی تبدیل می‌کند و مدار انتگرال‌گیر دوم با گردکردن نقاط شکل‌موج مثلثی، یک شکل‌موج خروجی موج سینوسی با یک دامنه‌ی بسیار کاهش‌یافته، تولید می‌کند.