فیلترهای مرتبه دوم

فیلترهای مرتبه دوم (دوقطبی) از دو بخش فیلتر RC تشکیل شده‌اند تا یک شیب منفی 40 دسی‌بل بر دهه در قسمت شیب‌دار ایجاد کنند.

چون آپ‌امپ به عنوان تقویت‌کننده منبع ولتاژ کنترل شده با ولتاژ استفاده می‌شود، فیلترهای مرتبه دوم به عنوان فیلترهای VCVS نیز نامیده می‌شوند. این فیلترها نوع مهم دیگری از طراحی فیلتر اکتیو هستند زیرا در کنار فیلترهای RC درجه اول اکتیو که قبلا به آنها پرداخته‌ایم، برای طراحی مدارات درجه بالاتر از آنها استفاده می‌شود.

در بخش مقالات فیلترهای آنالوگ، به طراحی فیلترهای پسیو و اکتیو پرداختیم و دیدیم که فیلترهای درجه اول را می‌توان به راحتی با استفاده از یک شبکه RC اضافی در مسیر ورودی یا فیدبک، به فیلترهای مرتبه دوم تبدیل کرد. پس می‌توانیم فیلترهای مرتبه دوم را به سادگی به این صورت تعریف کنیم: «دو فیلتر مرتبه ۱ که همراه با تقویت‌کننده کسکود شده‌اند».

اکثر طرح‌های فیلتر درجه دوم معمولا به نام مخترع خود نامگذاری می‌شوند و رایج‌ترین انواع فیلترها عبارتند از: باترورث، چبیشف، بسل و سلن-کی. همه این نوع فیلترها با ساختارهای زیر در دسترس هستند: فیلتر پایین‌گذر، فیلتر بالاگذر، فیلتر میان‌گذر و فیلتر میان‌نگذر (ناچ)، و از آنجایی که همه فیلترهای درجه یا مرتبه دوم هستند، شیب ۴۰ دسی‌بل بر دهه در قسمت شیبدار دارند.

طراحی فیلتر سلن-کی یکی از شناخته‌شده‌ترین و محبوب‌ترین طرح‌های فیلتر مرتبه دوم است که تنها به یک تقویت‌کننده عملیاتی برای کنترل گین و چهار جز پسیو RC برای تنظیمات دیگر نیاز دارد.

اکثر فیلترهای اکتیو فقط از آپ امپ‌ها، مقاومت‌ها و خازن‌ها تشکیل می‌شوند که نقطه فرکانس قطع با استفاده از فیدبک تنظیم می‌شود که نیاز به سلف‌هایی را که در مدارهای فیلتر مرتبه اول پسیو استفاده می‌شود، از بین می‌برد.

فیلترهای اکتیو مرتبه دوم (دو قطبی) اعم از پایین‌گذر یا بالاگذر، در الکترونیک اهمیت دارند زیرا می‌توانیم از آنها برای طراحی فیلترهای درجه بالاتر با شیب تیز قسمت شیب‌دار استفاده کنیم و با کسکود کردن فیلترهای مرتبه اول و دوم، فیلترهای آنالوگ مرتبه nام فرد یا زوج را می‌توان تا هر درجه معقول ساخت.

فیلتر پایین‌گذر مرتبه دوم

طراحی فیلترهای پایین‌گذر مرتبه دوم آسان است و به طور گسترده در بسیاری از کاربردها استفاده می‌شود. ساختار اولیه برای فیلتر پایین‌گذر درجه دوم سلن-کی (دو قطبی) به شرح زیر است:

فیلتر پایین گذر درجه دوم

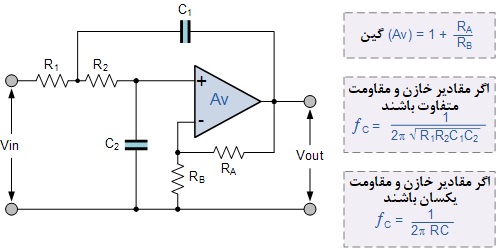۱. فیلتر پایین گذر درجه دوم

این مدار فیلتر پایین‌گذر درجه دوم دارای دو شبکه RC به صورت R۱-C۱ و R۲-C۲ است که به فیلتر خواص پاسخ فرکانسی آن را می‌دهد. طراحی فیلتر بر اساس یک ساختار آپ‌امپ غیر معکوس است، بنابراین گین یا بهره‌ی فیلترها، AV همیشه بزرگتر از ۱ خواهد بود. همچنین آپ‌امپ دارای امپدانس ورودی بالایی است که به این معنی است که می‌توان آن را به راحتی برای ارائه طرح‌‌های پیچیده‌تر فیلتر با مدارهای فیلتر اکتیو دیگر کسکود کرد.

پاسخ فرکانسی نرمالیزه فیلتر پایین‌گذر درجه دوم توسط شبکه RC تثبیت می‌شود و به طور کلی با پاسخ فرکانسی فیلتر درجه اول یکسان است. تفاوت اصلی بین یک فیلتر پایین‌گذر درجه 1 و 2 این است که با افزایش فرکانس کاری بالاتر از فرکانس قطع fC، شیب قسمت شیب‌دار در باند توقف دو برابر فیلترهای درجه اول یعنی ۴۰ دسی‌بل بر دهه یا ۱۲ دسی‌بل بر اکتاو همچون شکل زیر خواهد بود.

پاسخ فرکانسی نرمالیزه فیلتر پایین‌گذر

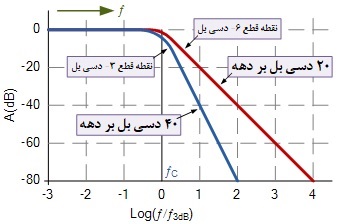۲. پاسخ فرکانسی نرمالیزه فیلتر پایین‌گذر

نمودار بد پاسخ فرکانسی بالا، اساسا مشابه فیلتر درجه 1 است. تفاوت این بار در شیب قسمت شیب‌دار است که منفی 40 دسی‌بل بر دهه در باند توقف است. با این حال، فیلترهای درجه دوم بسته به گین ولتاژی مدار یا Q در نقطه فرکانس قطع، می‌توانند پاسخ‌های مختلفی را نشان دهند.

در فیلترهای مرتبه دوم اکتیو معمولا از ضریب میرایی ζ (زتا) که معکوس Q است استفاده می شود. هر دو Q و ζ  به طور مستقل توسط گین تقویت‌کننده تعیین می شوند، بنابراین با کاهش Q، ضریب میرایی افزایش می یابد. به عبارت ساده، یک فیلتر پایین‌گذر همیشه در طبیعت خود پایین‌گذر خواهد بود، اما می‌تواند یک پیک تشدید را در مجاورت فرکانس قطع نشان دهد، یعنی گین می‌تواند به سرعت به دلیل اثرات تشدید گین تقویت‌کننده افزایش یابد.

پس Q، ضریب کیفیت، «مقدار» این پیک تشدید را نشان می‌دهد، یعنی ارتفاع و باریکی آن در اطراف نقطه فرکانس قطع (fC). اما گین فیلتر میزان فیدبک آن را نیز تعیین می‌کند و بنابراین تاثیر بسزایی در پاسخ فرکانسی فیلتر دارد.

به طور کلی برای حفظ پایداری، گین فیلترهای اکتیو نباید بیشتر از ۳ باشد و به بهترین وجه به صورت زیر بیان می‌شود:

ضریب کیفیت یا Q

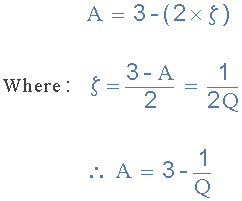
پس می‌بینیم که گین فیلتر یا A یک تقویت‌کننده غیرمعکوس باید بین مقادیر 1 و 3 باشد (مقدار ضریب میرایی بین صفر و 2). بنابراین، مقادیر بالای Q یا مقادیر پایین ζ موجب ایجاد پیک زیاد در پاسخ فرکانسی و شیب اولیه سریع‌تر در قسمت شیب‌دار همچون شکل زیر می‌شود.

پاسخ دامنه فیلتر درجه دوم

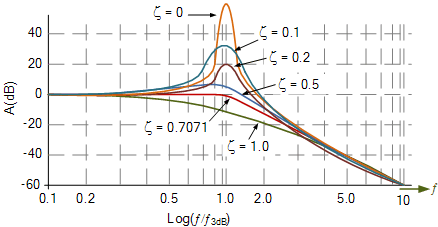۳. پاسخ دامنه فیلتر درجه دوم

پاسخ دامنه فیلتر پایین‌گذر درجه دوم برای مقادیر مختلف ضریب میرایی ζ متفاوت است. هنگامی که ζ = ۱.۰ یا بیشتر (۲ حداکثر است) فیلتر به چیزی تبدیل می‌شود که به آن «بیش از حد میرا» می‌گویند و پاسخ فرکانسی یک منحنی مسطح طولانی را نشان می‌دهد. هنگامی که ζ = ۰، خروجی فیلتر به شدت در نقطه فرکانس قطع بیشترین پیک را خواهد داشت که شبیه به یک نقطه تیز است که گفته می‌شود فیلتر «کم میرا» است.

پس باید مقدار ζ در جایی بین صفر و ۲ وجود داشته باشد که پاسخ فرکانسی مقدار صحیحی داشته باشد و این نقطه وجود دارد. این نقطه زمانی اتفاق می‌افتد که ζ=۰.۷۰۷۱ شود و در این صورت فیلتر به طور بحرانی میرا می‌شود.

نکته دیگر این است که زمانی که مقدار فیدبک به 4 یا بیشتر می‌رسد، فیلتر به دلیل اثرات تشدید به خودی خود در نقطه فرکانس قطع شروع به نوسان می‌کند و فیلتر را به یک نوسان‌ساز تبدیل می‌کند. این اثر خود نوسان نامیده می‌شود. پس برای فیلتر درجه دوم پایین‌گذر، مقادیر Q و ζ نقش مهمی دارند.  

می‌توانیم از منحنی‌های پاسخ فرکانس نرمالیزه در بالا برای یک فیلتر درجه 1 (خط قرمز) متوجه شویم که گین باند عبور صاف می‌ماند (با نام حداکثر مسطح) تا زمانی که پاسخ فرکانسی به نقطه فرکانس قطع f=fr برسد که پس از این فرکانس، گین فیلتر که در فرکانس گوشه برابر با (√۲=۰.۷۰۷۱) است، کاهش می‌یابد. این نقطه به طور کلی به عنوان نقطه منفی ۳ دسی‌بل فیلتر شناخته می‌شود و برای یک فیلتر پایین‌گذر درجه اول ضریب میرایی برابر با یک خواهد بود (ζ=۱)

با این حال، این نقطه فرکانس قطع منفی 3 دسی‌بل به دلیل شیب تندتر 40 دسی‌بل بر دهه، در موقعیت فرکانسی متفاوتی برای فیلترهای درجه دوم خواهد بود (خط آبی).  به عبارت دیگر، فرکانس قطع fr با افزایش درجه فیلتر، موقعیت خود را تغییر می‌دهد. پس برای بازگرداندن نقطه منفی ۳ دسی‌بل در فیلترهای مرتبه دوم به همان موقعیت فیلتر درجه اول، باید کمی گین به فیلتر اضافه کنیم.

بنابراین برای طراحی فیلتر پایین‌گذر مرتبه دوم باترورث، بسل و چبیشف مقدار گین به ترتیب برابر با ۵۸۶/۱، ۲۶۸/۱ و ۲۳۴/۱ خواهد بود.

مثال اول فیلتر درجه دوم

یک فیلتر پایین‌گذر مرتبه دوم باید به کمک یک آپ‌امپ غیرمعکوس با مقادیر مقاومت و خازن برابر در مدار تعیین‌کننده فرکانس قطع آن طراحی شود. اگر مشخصات فیلتر به صورت  Q = 5 و ƒc = 159Hz داده شود، یک فیلتر پایین‌گذر مناسب طراحی کنید و پاسخ فرکانسی آن را رسم کنید.

ویژگی های داده شده:  R۱ = R۲، C۱ = C۲، Q = 5

از مدار بالا می‌دانیم که برای مقاومت و خازن‌های برابر، نقطه فرکانس قطع از فرمول زیر قابل محاسبه است:

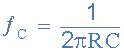
با انتخاب یک مقدار مناسب برای مقاومت مثلا ۱۰ کیلواهم، مقدار خازن به این صورت محاسبه می‌شود:

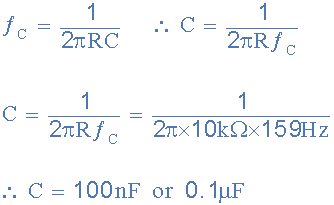
پس برای نقطه فرکانس قطع ۱۵۹ هرتز، مقاومت و خازن برابر با ۱۰ کیلو‌اهم و ۱/۰ میکروفاراد خواهند شد.

با داشتن مقدار Q=5 مقدار گین فیلتر به این صورت محاسبه می‌شود:

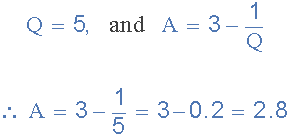
می‌دانیم که گین آپ‌امپ غیرمعکوس به صورت زیر است. پس مقدار مقاومت دیگر به این صورت محاسبه می‌شود:

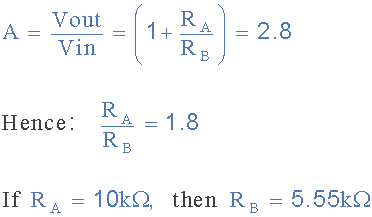
اگر مقدار RA=10kΩ باشد، پس مقدار RB برابر با ۵۵/۵ کیلواهم خواهد بود. بنابراین مدار نهایی برای فیلتر پایین‌گذر درجه دوم به این صورت خواهد بود:

فیلتر پایین‌گذر درجه دوم

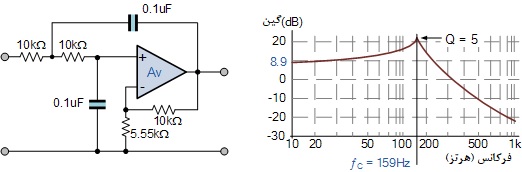۴. فیلتر پایین‌گذر درجه دوم

می‌بینیم که پیک منحنی پاسخ فرکانسی در فرکانس قطع به دلیل مقدار ضریب کیفیت بالا، Q = 5، کاملا واضح است. در این نقطه گین فیلتر به صورت Q × A = 14 یا حدود ۲۳+ دسی‌بل می‌شود که تفاوت زیادی با مقدار محاسبه شده ۸/۲ (۹/۸ دسی‌بل) دارد.

اما در بسیاری از کتاب‌ها نوشته شده است که گین فیلتر در نقطه فرکانس قطع نرمالیزه باید در نقطه منفی ۳ دسی‌بل باشد. کاهش قابل توجه مقدار Q به عدد ۷۰۷۱/۰منجر به افزایش گین تا عدد ۵۸۶/۱ می‌شود و باعث می شود پاسخ فرکانسی در باند عبور در صافترین حالت خود قرار داشته باشد و همچون پاسخ فیلتر باترورث درجه دوم، دارای تضعیف منفی ۳ دسی‌بل در نقطه فرکانس قطع است.

تاکنون دیده‌ایم که فیلترهای درجه دوم می‌توانند نقطه فرکانس قطع خود را در هر مقدار دلخواه تنظیم کنند، اما می‌توانند با توجه ضریب میرایی ، از این مقدار دلخواه فاصله بگیرند. طرح‌های فیلتر اکتیو، با کسکود کردن بخش‌های فیلتر با هم، ساخت فیلتر تا هر مقدار درجه معقول را ممکن می‌سازد.  

در عمل، هنگام طراحی فیلترهای پایین‌گذر درجه n، مطلوب است که فرکانس قطع را برای قسمت درجه اول (اگر درجه فیلتر فرد باشد) تنظیم کنید و ضریب میرایی و گین مربوطه را برای هر یک از بخش‌های درجه دوم تنظیم کنید تا پاسخ کلی صحیح به دست آید. برای سهولت در طراحی فیلترهای پایین‌گذر، مقادیر ζ، Q  و A به صورت جدول‌بندی‌شده همانطور که در آموزش فیلتر باترورث خواهیم دید، برای فیلترهای اکتیو موجود است. توجه شما را به مثال دیگری دعوت می‌کنم.

مثال دوم فیلتر درجه دوم

یک فیلتر پایین‌گذر درجه دوم با تقویت‌کننده غیرمعکوس طراحی کنید که دارای ویژگی‌های زیر باشد:

Q = 1, and ƒc = 79.5Hz

همانطور که می‌دانیم فرمول فرکانس گوشه به صورت زیر است:

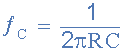
با انتخاب یک مقدار مناسب برای مقاومت مثلا ۱ کیلواهم، مقدار خارن به صورت زیر محاسبه می‌شود:

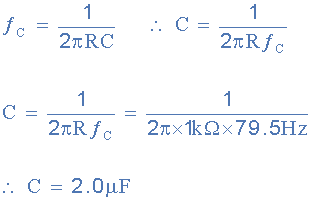
پس برای نقطه فرکانس قطع ۵/۷۹ هرتز، مقاومت و خازن برابر با ۱ کیلو‌اهم و ۲ میکروفاراد خواهند شد.

با داشتن مقدار Q=۱ مقدار گین فیلتر به این صورت محاسبه می‌شود:

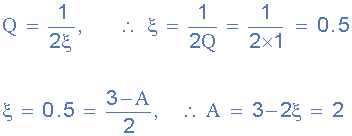
می‌دانیم که گین آپ‌امپ غیرمعکوس به صورت زیر است پس مقدار مقاومت دیگر به این صورت محاسبه می‌شود:

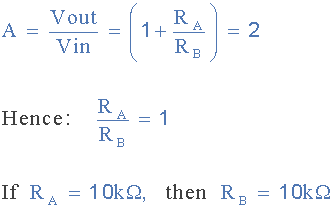
اگر مقدار RA=10kΩ باشد، پس مقدار RB برابر با ۱ کیلواهم خواهد بود. بنابراین مدار نهایی برای فیلتر پایین‌گذر درجه دوم با مقدار Q برابر با ۱ و فرکانس قطع ۵/۷۹ به این صورت خواهد بود:

مدار فیلتر پایین‌گذر

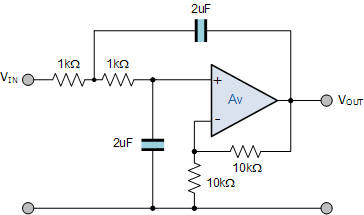۵. مدار فیلتر پایین‌گذر

فیلتر بالاگذر درجه دوم

تفاوت بسیار کمی بین ساختار فیلتر پایین‌گذر درجه دوم و ساختار فیلتر بالاگذر درجه دوم وجود دارد، تنها چیزی که تغییر کرده است موقعیت مقاومت‌ها و خازن‌ها مطابق شکل است.

فیلتر بالاگذر درجه دوم

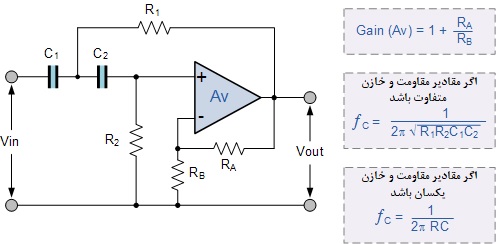۶. فیلتر بالاگذر درجه دوم

از آنجایی که فیلترهای درجه دوم بالا‌گذر و پایین‌گذر، مدارهای مشابهی دارند اما موقعیت مقاومت‌ها و خازن‌ها با هم عوض شده‌اند، روش‌های طراحی و مقیاس‌بندی فرکانس برای فیلتر بالاگذر دقیقا مانند فیلتر پایین‌گذر قبلی است. بنابراین نمودار بد برای یک فیلتر بالاگذر درجه دوم به صورت زیر می‌باشد:

پاسخ فرکانسی نرمالیزه فیلتر بالا‌گذر

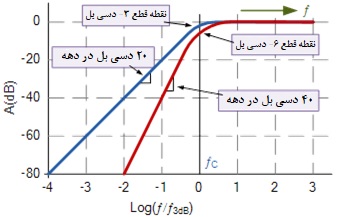۷. پاسخ فرکانسی نرمالیزه فیلتر بالا‌گذر

همانند فیلتر پایین‌گذر قبلی، شیب قسمت شیب‌دار در باند توقف 40 دسی‌بل بر دهه است. در دو مدار فوق، مقدار گین ولتاژ آپ‌امپ(AV) توسط شبکه فیدبک تقویت‌کننده تنظیم می‌شود. این فقط گین را برای فرکانس‌های موجود در باند عبور فیلتر مشخص می‌کند. می‌توانیم انتخاب کنیم که خروجی را تقویت کنیم و این مقدار گین را با هر مقداری که برای هدف ما مناسب است تنظیم کنیم و این گین را به عنوان یک ثابت K تعریف کنیم. فیلترهای سلن-کی درجه دوم به عنوان فیلترهای فیدبک مثبت نیز شناخته می‌شوند زیرا خروجی به پایه مثبت آپ‌امپ باز می‌گردد. این نوع طراحی فیلتر اکتیو معروف است زیرا تنها به یک آپ‌امپ نیاز دارد و در نتیجه نسبتا ارزان است.