اتصال سری مقاومت ها

هنگامی که مقاومت‌ها در یک خط به هم متصل شده و در نتیجه جریان مشترکی از آنها عبور کند، گفته می‌شود که به صورت سری به هم متصل شده‌اند.

مقاومت می‌توانند به صورت سری، موازی یا ترکیبی از هر دو به یکدیگر متصل شوند تا شبکه‌های مقاومت پیچیده‌تری تولید کنند که مقاومت معادل آن، ترکیب ریاضی مقادیر مقاومت‌های متصل به هم باشد.

مقاومت یک قطعه الکترونیکی بنیادی است که نه تنها می‌تواند برای تبدیل ولتاژ به جریان یا جریان به ولتاژ استفاده شود، بلکه با تنظیم صحیح مقدار آن می‌توان وزن متفاوتی روی جریان و یا ولتاژ تبدیل شده قرار داد تا بتوان از آن در کاربردها و مدارهای مرجع ولتاژ استفاده کرد.

مقاومت‌های سری یا شبکه‌های مقاومت پیچیده را می توان با یک مقاومت معادل واحد (REQ) یا امپدانس معادل (ZEQ) جایگزین کرد. بدون در نظر گرفتن ترکیب یا پیچیدگی شبکه مقاومت، همه مقاومت‌ها از قواعد اساسی تعریف شده توسط قانون اهم و قوانین مدار کیرشهف پیروی می کنند.

اتصال سری مقاومت‌ها

هنگامی که مقاومت‌ها در یک خط به هم متصل شوند، گفته می‌شود که به صورت سری به هم متصل شده‌اند. از آنجا که تمام جریان عبوری از مقاومت اول راه دیگری برای رفتن ندارد، باید از مقاومت دوم، سوم و غیره عبور کند. پس مقاومت‌های سری دارای یک جریان عبوری مشترک هستند، زیرا جریانی که از یک مقاومت عبور می‌کند باید از مقاومت‌های دیگر نیز بگذرد، زیرا فقط می‌تواند یک مسیر را طی کند.

پس مقدار جریانی که از مجموعه‌ای از مقاومت‌های سری عبور می‌کند، در تمام نقاط یک شبکه مقاومت سری یکسان خواهد بود. مثلا:

IR1 = IR2 = IR3 = IAB = 1mA

در مثال زیر، مقاومت‌های R۱، R۲ و R۳ به صورت سری بین دو نقطه A و B به هم متصل شده‌اند و جریان مشترک I از آن‌ها عبور می‌کند.

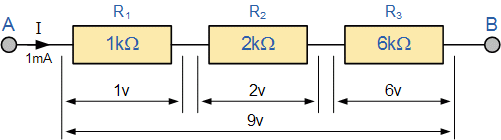مدار مقاومت سری

از آنجایی که مقاومت‌ها به صورت سری به یکدیگر متصل شده‌اند، جریان یکسانی از هر مقاومت در زنجیره عبور می‌کند و مقاومت کل مدار (RT) باید برابر با مجموع مقاومت‌های متصل به یکدیگر باشد. به این معنا که

RT = R۱ + R۲ + R۳

و با در نظر گرفتن مقادیر مقاومت‌ها در مثال بالا، مقاومت معادل کل REQ به صورت زیر محاسبه می‌شود:

REQ = R۱ + R۲ + R۳ = 1kΩ + 2kΩ + 6kΩ = 9kΩ

بنابراین می‌بینیم که می‌توانیم هر سه مقاومت بالا را فقط با یک مقاومت «معادل» جایگزین کنیم که مقدار آن ۹ کیلو اهم است.

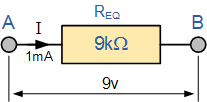
در صورتی که چهار، پنج یا حتی تعداد بیشتری از مقاومت‌ها در مدار سری بهم متصل شده باشند، مقاومت کل (یا معادل) RT، همچنان مجموع مقاومت‌های متصل به هم خواهد بود؛ هرچه مقاومت‌های بیشتری به سری اضافه شوند (بدون توجه به مقدار آنها)، مقدار مقاومت معادل نیز بیشتر می‌شود.

این مقاومت کل، به طور کلی به عنوان مقاومت معادل شناخته شده و به این صورت تعریف می‌شود: «یک مقدار مقاومت که می‌تواند هر تعداد مقاومت سری را بدون تغییر مقادیر جریان یا ولتاژ مدار جایگزین کند». پس معادله داده شده برای محاسبه مقاومت کل مدار هنگام اتصال سری مقاومت‌ها به صورت زیر ارائه می‌شود:

معادله مقاومت سری

Rtotal = R۱ + R۲ + R۳ + … + Rn

پس توجه داشته باشید که تاثیر مقاومت کل یا معادل RT در مدار، همان تاثیر ترکیب اصلی مقاومت‌ها است، چراکه مقدار آن، مجموع جبری مقادیر مقاومت‌های سری است.

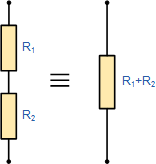
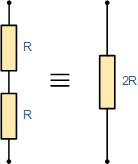
یک نکته مهم که باید در مورد مقاومت‌ها در یک شبکه سری به خاطر بسپارید این است که درستی ریاضیات خود را بررسی کنید. مقدار مقاومت کل (RT) دو یا چند مقاومت متصل به یکدیگر همواره از مقدار بزرگ‌ترین مقاومت در زنجیره، بزرگ‌تر خواهد بود. در مثال بالا RT = 9kΩ در حالی که بیشترین مقدار مقاومت در مدار تنها 6kΩ است.

ولتاژ مقاومت سری

ولتاژ دو سر هر مقاومت در اتصال سری، قوانین متفاوتی را نسبت به جریان سری دنبال می‌کند. در مدار بالا می‌دانیم که ولتاژ کل منبع تغذیه برابر با مجموع اختلافات پتانسیل R۱، R۲ و R۳ است:

VAB = VR1 + VR2 + VR3 = 9V

با استفاده از قانون اهم می‌توان ولتاژ دو سر هر مقاومت را به صورت زیر محاسبه کرد:

ولتاژ دو سر R۱: VR1 = IR۱ = 1mA × 1kΩ = 1V

ولتاژ دو سر R۲: VR2 = IR۲ = 1mA × 2kΩ = 2V

ولتاژ دو سر R۳: VR3 = IR۳ = 1mA × 6kΩ = 6V

در نتیجه، ولتاژ کل VAB برابر است با حاصل جمع این سه ولتاژ یعنی 1V + 2V + 6V = 9V که این همان ولتاژ منبع تغذیه است. پس مجموع اختلاف پتانسیل دو سر مقاومت‌ها برابر است با اختلاف پتانسیل کل مجموعه که در مثال بالا این عدد 9 ولت است.

معادله داده شده برای محاسبه ولتاژ کل در یک مدار سری، که با جمع تمام ولتاژهای منفرد به دست می‌آید، به صورت زیر است:

VTotal = VR1 + VR2 + VR3 + … + VN

پس شبکه‌های مقاومت سری را می‌توان به عنوان «تقسیم کننده ولتاژ» در نظر گرفت. یک مدار مقاومت سری که دارای N مقاومت است، تعداد N ولتاژ مختلف در طول خود خواهد داشت در حالی که جریان در طول مسیر ثابت است.

با استفاده از قانون اهم، ولتاژ، جریان یا مقاومت در هر مدار سری به راحتی محاسبه می‌شود. می‌توان مقاومت مدار سری را بدون تاثیر بر مقدار مقاومت کل، جریان یا هر مقاومت، تعویض کرد.

مثال ۱

با استفاده از قانون اهم، مقاومت معادل، جریان، افت ولتاژ و توان هر مقاومت را برای هر مقاومت در مدار سری زیر محاسبه کنید.

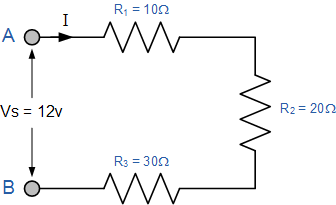
همه داده‌ها را می‌توان با استفاده از قانون اهم به دست آورد و برای راحتی بیشتر، می‌توانیم این داده‌ها را به صورت جدول ارائه دهیم.

پس در مدار بالا، RT = 60Ω، IT = 200mA، VS = 12V و PT = 2.4W است.

مدار تقسیم ولتاژ

از مثال بالا می توان دریافت که اگرچه ولتاژ تغذیه 12 ولت است، ولتاژهای مختلف، یا به عبارت دیگر افت ولتاژ، در هر مقاومت در شبکه سری ظاهر می‌شود. اتصال سری مقاومت‌ها به این شکل به یک منبع تغذیه DC یک مزیت عمده دارد. ولتاژهای مختلفی در هر مقاومت ظاهر شده و یک مدار بسیار مفید به نام شبکه تقسیم ولتاژ تولید می‌شود.

این مدار ساده، ولتاژ منبع تغذیه را به تناسب هر مقاومت در زنجیره سری، با مقدار افت ولتاژ که توسط مقدار مقاومت‌ها تعیین می‌شود، تقسیم می‌کند و همانطور که اکنون می‌دانیم، جریان در طول یک مدار مقاومت سری، برای همه مقاومت‌ها یکسان است. بنابراین یک مقاومت بزرگ‌تر، افت ولتاژ بیشتر و یک مقاومت کوچک‌تر، افت ولتاژ کمتری خواهد داشت.

مدار مقاومتی سری که در بالا نشان داده شده، یک شبکه تقسیم ولتاژ ساده را تشکیل می دهد که در آن سه ولتاژ 2 ولت، 4 ولت و 6 ولت از یک منبع تغذیه 12 ولت تولید می‌شود. قانون ولتاژ کیرشهف بیان می کند که «ولتاژ تغذیه در یک مدار بسته برابر است با مجموع تمام افت ولتاژها (I×R) در طول مدار». این قانون کاربردهای خوبی برای ما دارد.

قانون تقسیم ولتاژ به ما اجازه می دهد تا از اثرات تناسب مقاومت برای محاسبه اختلاف پتانسیل دو سر هر مقاومت، بدون در نظر گرفتن جریان عبوری از مدار سری، استفاده کنیم. در ادامه یک «مدار تقسیم ولتاژ» معمول نشان داده شده است.

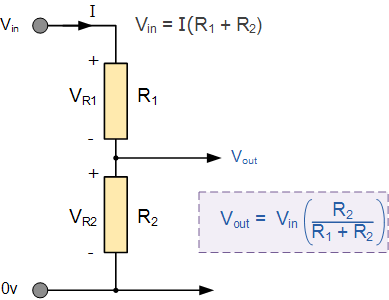شبکه تقسیم ولتاژ

مدار شکل بالا تنها شامل دو مقاومتR۱ وR۲ است که به صورت سری به ولتاژ تغذیه Vin متصل شده‌اند. یک طرف ولتاژ منبع تغذیه به مقاومت R۱ متصل شده و خروجی ولتاژ، Vout از مقاومت R۲ گرفته شده است. مقدار این ولتاژ خروجی با فرمول مربوطه محاسبه می‌شود.

اگر مقاومتهای بیشتری به صورت سری به مدار وصل شوند، ولتاژهای مختلفی دو سر هر مقاومت، با توجه به مقادیر مقاومت (R) آنها ظاهر می‌شود (قانون اهم I×R) که نقاط ولتاژ متفاوت اما کوچکتری را از یک منبع تغذیه ارائه می‌دهند.

بنابراین اگر سه یا چند مقاومت در زنجیره سری داشته باشیم، هنوز هم می‌توانیم از فرمول تقسیم کننده ولتاژ،که حال برای ما شناخته شده است، برای یافتن افت ولتاژ در هر یک استفاده کنیم. مدار زیر را در نظر بگیرید.

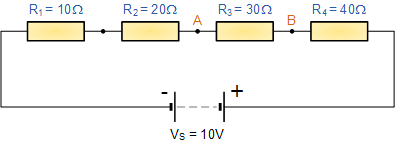
مدار تقسیم کننده ولتاژ بالا چهار مقاومت سری را نشان می‌دهد. افت ولتاژ در نقاط A و B را می‌توان با استفاده از فرمول تقسیم ولتاژ به شرح زیر محاسبه کرد:

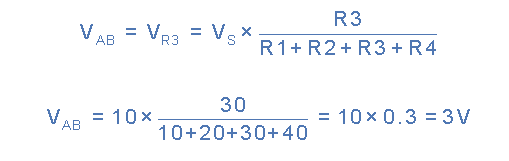
همچنین می‌توانیم همین ایده را برای گروهی از مقاومت‌ها در زنجیره سری اعمال کنیم. به عنوان مثال، اگر بخواهیم افت ولتاژ R۲ و R۳ را با هم پیدا کنیم، مقادیر آنها را در صورت کسر فرمول بالا جایگزین می‌کنیم و در این حالت به جواب 5 ولت (2V + 3V) می‌رسیم.

در این مثال بسیار ساده، ولتاژها اعداد رند هستند زیرا افت ولتاژ در یک مقاومت، متناسب با مقاومت کل است و از آنجا که مقاومت کل (RT) در این مثال برابر با 100 اهم یا 100% است، مقاومت R۱ ده درصد از RT است، بنابراین 10% ولتاژ منبع VS دو سر آن ظاهر می شود و به همین ترتیب، 20% ولتاژ منبع دو سر مقاومت R۲، 30% دو سر مقاومت R۳ و 40% دو سر مقاومت R۴ ظاهر می‌شود. استفاده از قانون ولتاژ کیرشهف (KVL) در مسیر حلقه بسته، این موضوع را تایید می‌کند.

حال فرض کنید که می‌خواهیم از مدار تقسیم ولتاژ با دو مقاومت استفاده کنیم تا ولتاژ کوچک‌تری از ولتاژ تغذیه بزرگ‌تر تولید کنیم تا یک مدار الکترونیکی خارجی را تغذیه کنیم. فرض کنید ما یک منبع تغذیه 12V DC داریم و مدار ما که دارای امپدانس 50Ω است، تنها به 6V یعنی نیمی از ولتاژ نیاز دارد.

اتصال دو مقاومت برابر، مثلاً هر کدام 50Ω، به عنوان یک شبکه تقسیم ولتاژ به منبع تغذیه 12V، این کار را بسیار خوب انجام می‌دهد، تا زمانی که مدار بار را به شبکه وصل کنیم. دلیل این امر آن است که اثر بارگذاری مقاومت RL، که به طور موازی به R۲ متصل شده است، نسبت مقاومت‌های سری و در نتیجه افت ولتاژ آنها را تغییر می‌دهد. این اثر در مثال زیر نشان داده شده است.

مثال ۲

افت ولتاژ نقاط X و Y را محاسبه کنید

الف) بدون اتصال RL

ب) با اتصال RL

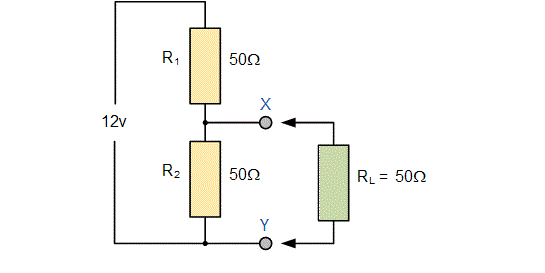
الف) بدون اتصال RL

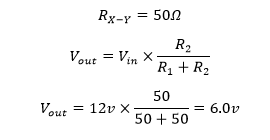
ب) با اتصال RL

 (مقاومت‌ها به صورت موازی متصل شده‌اند)

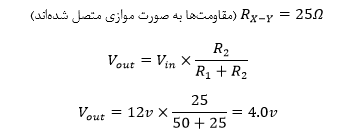
همانطور که مشاهده می‌کنید، ولتاژ خروجی Vout، بدون اتصال مقاومت بار، ولتاژ خروجی مورد نیاز ۶ ولت را به ما می‌دهد، اما همان ولتاژ خروجی پس از اتصال بار تا ۴ ولت کاهش می‌یابد (به دلیل اتصال موازی مقاومت‌ها).

پس می‌ببینیم که یک شبکه تقسیم ولتاژ بارگذاری شده، ولتاژ خروجی خود را در نتیجه این اثر بارگذاری تغییر می‌دهد، زیرا ولتاژ خروجی Vout با نسبت R۱ به R۲ تعیین می‌شود. با این حال، با نزدیک شدن مقاومت بار RL به سمت بی نهایت (∞)، این اثر بارگیری کاهش می یابد و نسبت ولتاژ Vout/Vs با اضافه شدن بار در خروجی تحت تاثیر قرار نمی‌گیرد. پس هرچه امپدانس بار بیشتر باشد، اثر بارگذاری بر روی خروجی کمتر است.

اثر کاهش سطح سیگنال یا ولتاژ به عنوان میرایی شناخته می‌شود، بنابراین هنگام استفاده از شبکه تقسیم ولتاژ باید دقت کرد. این اثر بارگذاری را می‌توان با استفاده از پتانسیومتر به جای مقاومت ثابت جبران و بر اساس نیاز تنظیم کرد. این روش همچنین تلورانس‌های مختلف مقاومت‌های استفاده شده در تقسیم کننده ولتاژ را جبران می‌کند.

یک مقاومت متغیر، پتانسیومتر یا با نام رایج تر pot، نمونه خوبی از یک تقسیم کننده ولتاژ با چند مقاومت در یک بسته واحد است، زیرا می‌توان آن را هزاران مقاومت کوچک سری در نظر گرفت. در اینجا یک ولتاژ ثابت به دو پایه ثابت خارجی اعمال شده و ولتاژ خروجی متغیر از ترمینال وسط (که به آن wiper نیز می‌گویند) گرفته می‌شود. پتانسیومترهای با تعداد دور بیشتر امکان کنترل دقیق‌تر ولتاژ خروجی را فراهم می‌کنند.

مدار تقسیم ولتاژ ساده‌ترین راه تولید ولتاژ پایین‌تر از ولتاژ بالاتر و مکانیسم اصلی کار پتانسیومتر است.

علاوه بر محاسبه ولتاژ تغذیه کمتر، از فرمول تقسیم ولتاژ می‌توان در تجزیه و تحلیل مدارهای مقاومتی پیچیده‌تر، که شامل شاخه‌های سری و موازی هستند، نیز استفاده کرد. از فرمول تقسیم ولتاژ می‌توان برای تعیین افت ولتاژ در یک شبکه DC بسته یا به عنوان بخشی از قوانین مختلف تجزیه و تحلیل مدار، مانند قضیه‌های کیرشهف یا تونن، استفاده کرد.

کاربردهای اتصال سری مقاومت‌ها

دیدیم که می‌توان از اتصال سری مقاومت‌ها برای تولید ولتاژهای مختلف در مقاومت‌ها استفاده کرد؛ این نوع شبکه مقاومت برای تولید شبکه تقسیم ولتاژ بسیار مفید است. اگر یکی از مقاومت‌ها در مدار تقسیم ولتاژ بالا را با یک سنسور مانند ترمیستور، مقاومت وابسته به نور (مقاومت نوری، LDR) یا حتی یک سوئیچ جایگزین کنیم، می‌توانیم یک مقدار آنالوگ را که توسط سنسور دریافت می‌شود به سیگنال الکتریکی مناسبی تبدیل کنیم که اندازه گیری داشته باشد.

به عنوان مثال، مدار ترمیستور زیر دارای مقاومت 10kΩ در دمای 25°C و مقاومت 100Ω در دمای 100°C است. ولتاژ خروجی (Vout) را برای هر دو دما محاسبه کنید.

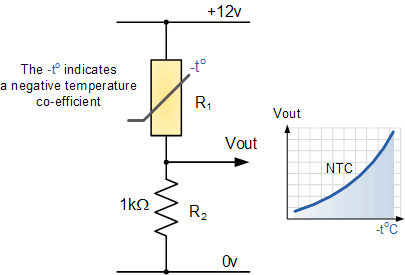مدار ترمیستور

دمای ۲۵ درجه سانتی گراد:

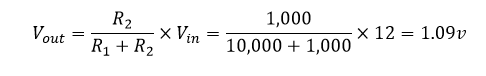
دمای ۱۰۰ درجه سانتی گراد:

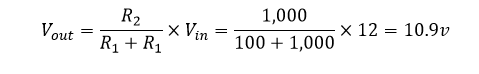
بنابراین با تغییر مقاومت ثابت 1kΩ، R۲، در مدار ساده بالا به یک مقاومت متغیر یا پتانسیومتر، می توان یک نقطه تنظیم خاص ولتاژ خروجی را در محدوده دمای وسیع‌تری به دست آورد.

خلاصه اتصال سری مقاومت‌ها

بنابراین برای جمع بندی: هنگامی که دو یا چند مقاومت پشت سر هم در یک شاخه واحد به یکدیگر متصل شوند، گفته می‌شود مقاومت‌ها سری هستند. مقاومت‌های سری جریان یکسانی دارند، اما افت ولتاژ دو سر آنها یکسان نیست، چراکه بر اساس قانون اهم (V = I×R)، مقادیر متفاوت آنها افت ولتاژ متفاوتی را در هر مقاومت ایجاد می کند. پس مدارهای سری تقسیم کننده ولتاژ هستند.

در یک شبکه مقاومت سری، مقادیر مقاومت‌ها با هم جمع می‌شوند تا یک مقاومت معادل (RT) از ترکیب سری ایجاد کنند. مقاومت‌ها در یک مدار سری می‌توانند بدون تاثیر بر مقاومت کل، جریان یا توان هر مقاومت یا مدار تعویض شوند.

در آموزش بعدی در مورد مقاومت‌ها، اتصال موازی مقاومت‌ها را بررسی خواهیم کرد و ثابت می‌کنیم که مقاومت کل، حاصل جمع معکوس مقدار مقاومت‌ها و ولتاژ دو سر همه آنها یکسان است.