مدار RLC سری

مدار سری RLC، از یک مقاومت، یک خازن و یک سلف؛ که به صورت سری به یک منبع تغذیه متناوب متصل شده‌اند، تشکیل می‌شود.

تا این‌جا مشاهده کردیم که سه عنصر پسیو اصلی از: مقاومت‌، اندوکتانس (ضریب خودالقایی) و ظرفیت خازنی، هنگام اتصال به یک منبع تغذیه متناوب سینوسی، روابط فازی بسیاری متفاوتی با یکدیگر دارند.

در  یک مقاومت اهمی خالص، شکل‌موج‌های ولتاژ، “هم‌فاز” با جریان می‌باشند. در  یک اندوکتانس خالص، شکل‌موج ولتاژ “پیشرو”تر از جریان با زاویه °90 است که  با عبارت ELI بیان می‌شود و در یک ظرفیت‌خازنی خالص، شکل‌ موج ولتاژ با  زاویه °90 “عقب‌”‌تر از جریان است؛ که عبارت ICE  برای بیان آن استفاده  می‌گردد.

این اختلاف فاز (φ) بستگی به مقدار راکتیو عناصر مورد استفاده دارد و تاکنون باید بدانیم که در صورتی‌که عنصر مدار مقاومتی باشد؛ راکتانس (X) صفر بوده و اگر عنصر مدار القایی باشد؛ مثبت و در صورت خازنی بودن آن، راکتانس منفی خواهد بود که به ما امپدانس حاصل زیر را خواهد داد:

امپدانس المان های RLC

المان	مقاومت (R)	راکتانس (X)	امپدانس (Z)
مقاومت	R	۰
سلف	۰	ωL
خازن	۰

به‌جای تجزیه‌ و‌ تحلیل هر عنصر پسیو به طور جداگانه، می‌توانیم هر سه را با هم در یک مدار RLC ترکیب کنیم.

تجزیه‌و‌تحلیل مدار سری RLC، همان است که برای سری دوگانه مدارهای RL و RC بررسی شد؛ با این تفاوت که باید اندازه‌های XL و  XC را در نظر بگیریم تا بتوانیم راکتانس کلی مدار را پیدا کنیم. مدارهای سری  RLC، جزو مدارهای مرتبه دوم کلاس‌بندی می‌شوند؛ زیرا دارای دو عنصر ذخیره‌کننده انرژی، اندوکتانس (L) و ظرفیت‌خازنی (C) می‌باشند. مدار RLC زیر را در نظر بگیرید.

مدار سری RLC

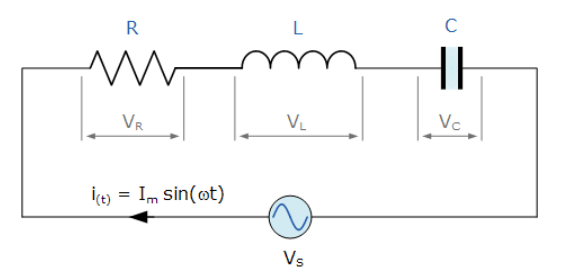1. مدار RLC سری

مدار فوق، دارای یک‌ حلقه با یک جریان‌ لحظه‌ای بوده که درون  حلقه جاری است و برای هر عنصر مدار یکسان است. از آنجایی‌که که راکتانس‌های  القایی و خازنی ( XLو XC ) توابعی از فرکانس منبع  می‌باشند؛درنتیجه، پاسخ فرکانسی یک مدار سری RLC با فرکانس (f) متغیر خواهد  بود. پس افت ولتاژ منفرد روی هر کدام از عناصر R،L و C “خارج فاز” خواهد  بود که به صورت زیر تعریف می‌گردد:

i(t) = Imax sin(ωt)

ولتاژ لحظه‌ای دوسر یک مقاومت خالص (VR) با جریان “هم‌فاز” خواهد بود.

ولتاژ لحظه‌ای دو سر سلف خالص (VL) از جریان °۹۰ “پیشرو”تر است.

ولتاژ لحظه‌ای دو سرخازن خالص (VC) از جریان °۹۰ “عقب‌مانده” تر است.

بنابراین، VL و VC در مخالفت با یک‌دیگر می‌باشند و °۱۸۰ خارج از فاز هستند.

برای مدار سری RLC بالا، می‌توان به‌صورت زیر نشان داد:

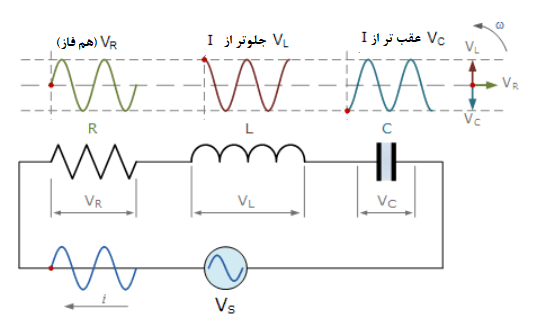2. ولتاژ لحظه ای المان‌های یک مدار RLC سری

دامنه‌ی ولتاژ منبع تغذیه دوسر هرکدام از سه عنصر مدار سری RLC، از سه عنصر منفرد ولتاژ VR ، VL و VC،   با جریان مشترک در هر سه عنصر تشکیل شده‌است. بنابراین، برای نمودارهای  برداری، بردار جریان به عنوان مرجع با سه بردار ولتاژ که برحسب این مرجع  ترسیم شده‌اند، در زیر نشان داده شده است:

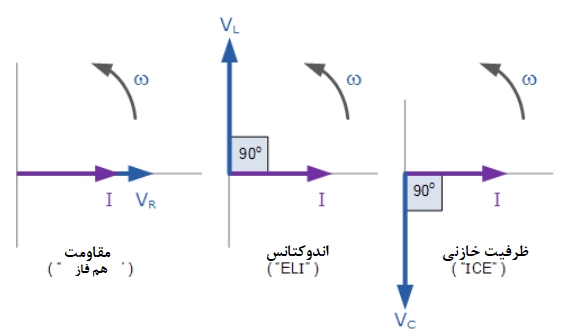3. بردار ولتاژ المانهای مدار  RLC

این بدان معناست، که ما نمی‌توانیم به سادگی VR ، VLو VC، را با یک‌دیگر جمع کنیم تا VS را برای این سه عنصر به دست آوریم؛ چون هر سه بردار ولتاژ درجهت‌های  متفاوت نسبت به بردار مرجع جریان دارند. بنابراین برای یافتن ولتاژ تغذیه  (VS)، باید مجموع فازور هر سه جز ولتاژ را، در ترکیب با یکدیگر به صورت برداری بدست آورد.

قانون  ولتاژ کیرشهف (KVL) برای حلقه‌ها و گره‌های مدار، بیان می‌کند؛ در اطراف  هر حلقه‌ی بسته، مجموع افت ولتاژ در اطراف حلقه برابر با مجموع EMF هاست.  درنتیجه اعمال این قانون به این سه ولتاژ به ما دامنه‌ی ولتاژ منبع تغذیه  (VS) را می‌دهد.

ولتاژهای لحظه‌ای برای مدار سری RLC

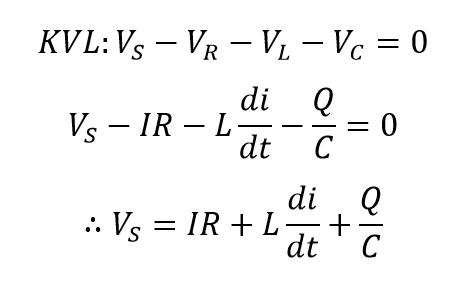
نمودار فازوری برای یک مدارهای سری RLC، با ترکیب سه فازور منفرد  ذکرشده در بالا و اضافه‌کردن این ولتاژها به صورت برداری به یکدیگر، تولید  می‌گردد. به دلیل این‌که جریان جاری در مدار، در هر سه عنصر مدار مشترک  است؛ می‌توان آن را به عنوان بردار مرجع برای رسم سه ولتاژ با زاویه‌های مربوطه، در نظر گرفت.

بردار حاصل (VS) را می‌توان با اضافه‌نمودن دو بردار  VL و  VC به یک‌دیگر و پس از آن، اضافه نمودن حاصل به‌دست آمده به بردار باقی‌مانده VR به دست‌آورد. زاویه حاصل بین VS و i، زاویه فاز مدار خواهد بود که در زیر آورده شده‌است.

دیاگرام فازور برای مدار سری RLC

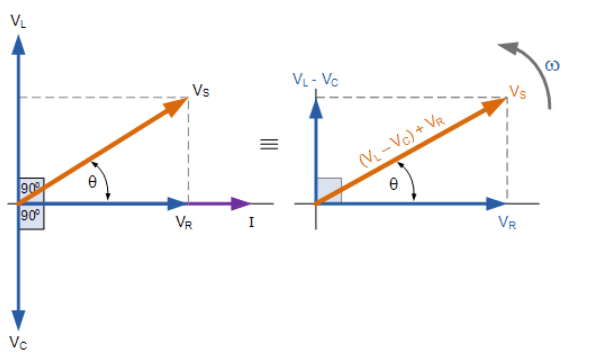3. دیاگرام فازور مدار سری RLC

از نمودار فازوری در سمت راست تصویر بالا، می‌توانیم ببینیم که بردارهای ولتاژ، یک مثلث مستطیل‌ شکل را تشکیل می‌دهند، که از وتر VS، محور افقی VR و محور عمودی VL-VC تشکیل شده‌است که سبب ساخته‌شدن مثلث ولتاژ می‌گردد و از قضیه فیثاغورث می‌توان در این مثلث استفاده نمود تا از نظر ریاضیاتی مقدار VS را همانطور که نشان داده‌شده، به دست آوریم.

مثلث ولتاژ برای مدار سری RLC

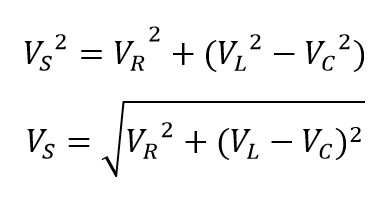
لطفا توجه داشته باشید که در هنگام استفاده از معادله‌بالا، ولتاژ راکتیو نهایی، همیشه باید مقدار مثبت داشته باشد؛ یعنی کوچکترین مقدار ولتاژ همیشه باید از بزرگترین مقدار ولتاژ گرفته‌شود. نمی‌توانیم یک مقدار منفی را به VR اضافه نماییم؛ محاسبه درست VL-VC یا VC-VL است. مقدار کوچک باید از مقدار بزرگ گرفته شود زیرا در غیراین‌صورت مقدار VS اشتباه خواهد بود.

از  بالا می‌دانیم که جریان، دامنه و فاز یکسانی در تمام عناصر مدار سری RLC  دارد؛ در نتیجه ولتاژ دوسر هر عنصر را از نظر ریاضیاتی، می‌توان نسبت به  جریان جاری در آن یافت. ولتاژ دوسر هر عنصر خواهد بود:

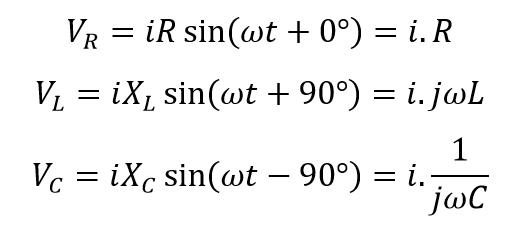
با جایگذاری این مقادیر در معادله فیثاغورث بالا برای مثلث ولتاژ خواهیم داشت:

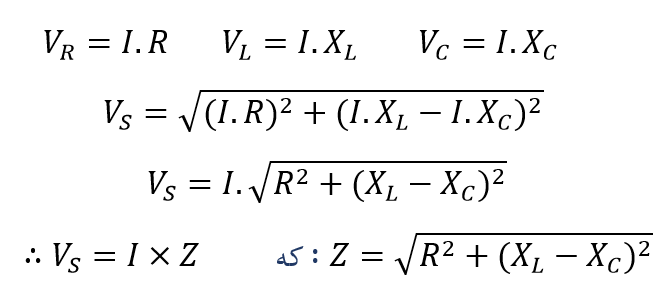
پس می‌توانیم ببینیم، که دامنه‌ی ولتاژ منبع متناسب با دامنه جریان عبوری از مدار است. این ثابت تناسب را امپدانس مدار می‌نامند؛ که درنهایت به مقاومت و راکتانس القایی و خازنی بستگی  دارد. پس در مدار سری RLC بالا، می‌توان دید که میزان مخالفت با جریان جاری  از این سه جز: XL ، XC و R با راکتانس XT برای هر مدار سری RLC، را می‌توان به صورت XT = XL – XC یا XT = XC – XL تعریف نمود، هرکدام که مقدار بزرگ‌تری داشته باشد. بنابراین، کل امپدانس مدار، وابسته به ولتاژ منبع و جریانی است که از آن می‌گذرد.

امپدانس مدار سری RLC

ازآن‌جایی‌که، سه بردار ولتاژ دارای فاز مخالف با یک‌دیگر می‌باشند؛ XL ، XC و R نیز باید دارای فاز مخالف با یک‌دیگر باشند و رابطه بین XL ، XC و R باید، مجموع برداری این سه جز باشد و به ما امپدانس کلی (Z) مدار سری  RLC را بدهد. این امپدانس مدار را می‌توان رسم کرد و با یک مثلث امپدانس  نشان داد که در زیر آورده شده است.

مثلث امپدانس برای مدار  RLC سری

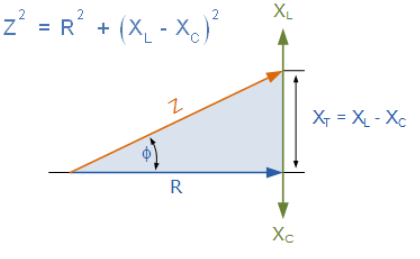4. مثلث امپدانس یک مدار RLC سری

امپدانس(Z) مدار سری RLC، به فرکانس زاویه‌ای (ω)، همانند XL و XC بستگی دارد. اگر راکتانس خازنی از راکتانس القایی بزرگتر باشد (XC>XL)  در نتیجه، راکتانس کلی مدار، خازنی است؛ که در نتیجه دارای زاویه فاز  پیشرو است. به همین‌ترتیب، اگر راکتانس القایی، بزرگتر از راکتانس خازنی  باشد (XL>XC)، درنتیجه راکتانس کلی مدار، القایی است؛ که درنتیجه، دارای زاویه فاز عقب‌ است. اگر هردو راکتانس دارای مقدار برابر باشند (XC=XL) فرکانس زاویه‌ای که در هرکدام رخ می‌دهد را فرکانس تشدید می‌گویند و اثر تشدیدی را ایجاد می‌کند که در مقاله دیگری با جزئیات بیشتری به آن خواهیم پرداخت.

پس،  اندازه جریان، به فرکانس اعمال‌شده به مدار سری RLC بستگی دارد. زمانی‌که،  امپدانس (Z) در حداکثر مقدار خود است، جریان حداقل بوده و به همین‌ترتیب،  هنگامی که Z، حداقل مقدار خود را دارد؛ جریان حداکثر است. بنابراین می‌توان  معادله‌ی فوق را برای امپدانس دوباره نوشت:

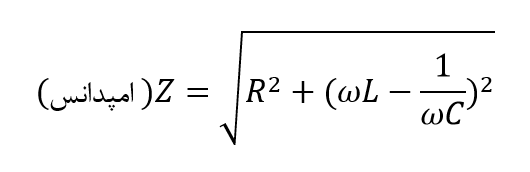
زاویه‌فاز (θ) بین ولتاژ منبع تغذیه (VS) و جریان (i)  همان زاویه‌ی بین Z و R در مثلث امپدانس است. این زاویه از نظر مقدار  می‌تواند مثبت یا منفی باشد؛ بسته به این‌که منبع ولتاژ در مدار پیشرو یا  عقب‌مانده از جریان باشد و می‌تواند به صورت ریاضیاتی از مقادیر اهمی مثلث  امپدانس محاسبه گردد.

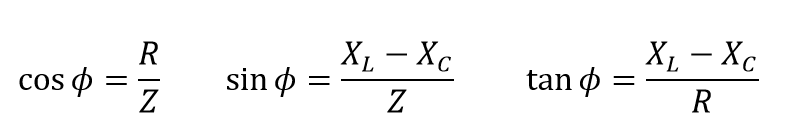
مثال شماره 1 - مدار سری RLC

یک مدار سری RLC، دارای یک مقاومت 12Ω و یک اندوکتانس 0.15H و یک  خازن100uFکه به صورت سری به یک منبع تغذیه 100V,50Hz متصل شده‌اند‌  می‌باشد . امپدانس کلی مدار، جریان مدار، ضریب توان را محاسبه نموده و  نمودار فازوری آن را رسم کنید.

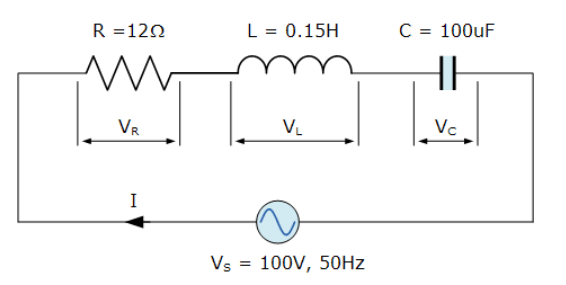5. مدار RLC سری - مثال 1

راکتانس القایی (XL):

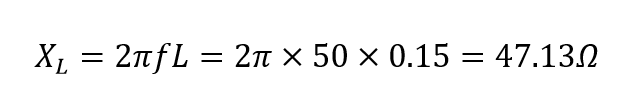
راکتانس خازنی (XC):

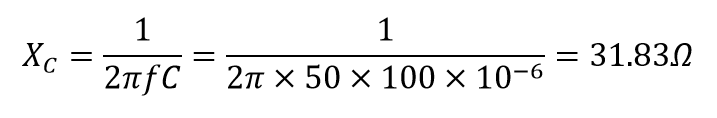
امپدانس مدار (Z):

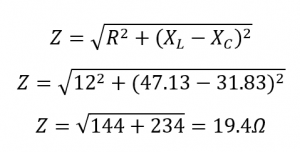
جریان مدار (I):

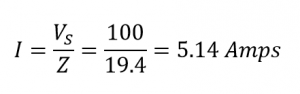
ضریب توان و زاویه‌فاز (θ)

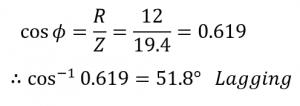
نمودار فازوری

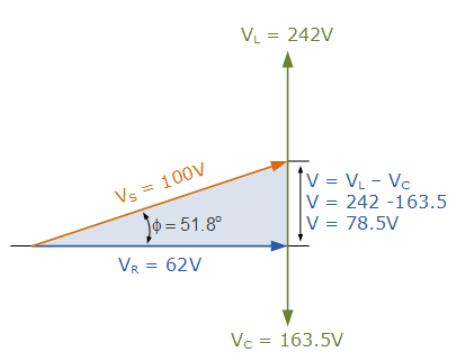۶. نمودار فازوری - مثال ۱

از آن‌جایی که، زاویه‌فاز (θ) با مقدار مثبت °51.8 محاسبه  شده‌است؛ راکتانس کلی مدار، باید القایی باشد. ازآن‌جایی که بردار جریان را  به‌عنوان بردار مرجع در مدار سری RLC در نظر گرفتیم؛ از این‌رو، جریان با  زاویه °51.8، از ولتاژ منبع تغذیه، “لگ” خواهد بود. درنتیجه می‌توانیم  بگوییم که زاویه‌فاز lagging بود که “ELI” را تایید می‌کند.

خلاصه مدار  RLC سری

در یک مدار RLC  سری ،تشکیل‌شده از مقاومت، سلف و خازن، ولتاژ منبع تغذی ه(VS)، جمع فازوری تشکیل‌شده از سه مولفه‌ی VR ، VLو VC با جریانی است که بین این سه مشترک است. از آنجایی‌که جریان بین تمام سه  عنصر مدار مشترک است؛ به عنوان مرجع افقی، زمانی‌که مثلث ولتاژ را  می‌سازیم؛ استفاده می‌گردد.

امپدانس مدار، میزان مخالفت کلی به جریان  جاری است. برای یک مدار سری RLC، مثلث امپدانس را می‌توان با تقسیم هر ضلع  مثلث ولتاژ بر جریان (I) رسم نمود. افت ولتاژ دوسر عنصر مقاومتی برابر با I*R خواهد بود؛ ولتاژ دوسر دو عنصر راکتیو برابر با  خواهد بود درحالی‌که، ولتاژ منبع برابر با I*X = I*XL – I*XC است. زاویه بین VS وI برابر با زاویه‌فاز (θ) است.

در  هنگام کار کردن با مدار سری RLC، که از چند مقاومت، ظرفیت خازنی یا  اندوکتانس خالص یا ناخالص تشکیل‌شده‌است؛ همه آن‌ها را می‌توان با یک‌دیگر  جمع کرده و یک جز واحد را تشکیل داد. امکان این جمع، برای تمام مقاومت‌هایی  که به یک‌دیگر اضافه می‌گردند …RT = ( R۱ + R۲ + R۳ ) و برای تمام اندوکتانس ها …(LT = ( L۱ + L۲ + L۳ و… خواهد بود؛ از این راه، یک مدار که از اجزای بسیاری تشکیل‌شده‌است را می‌توان به سادگی تا یک امپدانس تنها، کاهش داد.

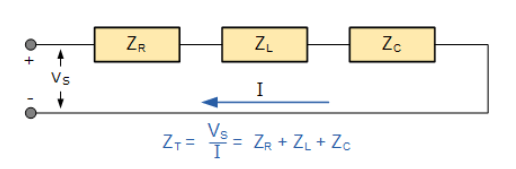7. اندوکتانس معادل مدار RLC سری

در مقاله بعدی، در مورد مدارهای  RLC موازی، به رابطه‌ی  ولتاژ-جریان هر سه عنصر؛ هنگامی که به یک دیگر در یک مدار موازی متصل  شده‌اند، و زمانی‌که شکل‌موج سینوسی AC حالت مانا به مدار متصل است؛ همراه  با نمایش نمودار فازوری مربوطه آن است؛ خواهیم پرداخت. هم‌چنین مفهوم ادمیتانس را برای اولین‌بار معرفی خواهیم نمود.