در این مقاله مبانی شکل موج سینوسی را بصورت مفصل شرح خواهیم داد. هنگامی که، یک جریان الکتریکی از طریق سیم یا هادی عبور میکند؛ یک میدان مغناطیسی دایره ای در اطراف سیم ایجاد میشود که قدرت آن وابسته به مقدار جریان است.
اگر این هادی تک سیم، در یک میدان مغناطیسی حرکت کرده و یا چرخانده شود، به دلیل حرکت هادی از طریق شار مغناطیسی، نیروی محرکه الکتریکی (EMF) درون هادی القا میشود.
از این طریق میتوان دریافت که میان الکتریسیته و مغناطیس رابطهای وجود دارد؛ زیرا مایکل فارادی اثر “القای الکترومغناطیسی” را کشف نمود و این اصل اساسی میباشد که ماشینها و ژنراتورهای الکتریکی از آن برای تولید یک شکل موج سینوسی برای منبع تغذیه استفاده میکنند.
زمانی که یک سیم رسانا در یک میدان مغناطیسی دائمی حرکت میکند؛ خطوط شار خود را قطع مینماید که سبب القای EMF در آن میشود.
با اینحال، اگر هادی به صورت موازی با میدان مغناطیسی حرکت نماید، به صورتی که در نقاط A و B قرار گیرد، هیج خط شاری قطع نمیگردد و هیچ نیروی محرکه الکتریکی به هادی القا نمیشود؛ درحالی که، اگر هادی با زاویه راست در میدان مغناطیسی حرکت نماید و در نقاط C و D، قرار گیرد، حداکثر مقدار شار مغناطیسی قطع میشود و حداکثر مقدار نیروی محرکه الکتریکی ناشی از آن تولید میگردد.
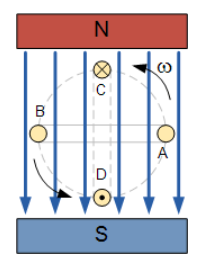
همچنین، زمانی که هادی میدان مغناطیسی را در زوایای مختلفی بین نقاط A و C ( 0 و 90°) قطع مینماید؛ مقدار EMF القا شده، در جایی بین مقدار صفر و حداکثر قرار خواهدگرفت. در نتیجه، مقدار EMF القاشده در یک هادی، به زاویه میان هادی و شارمغناطیسی و نیز قدرت میدان مغناطیسی بستگی دارد.
یک ژنراتورAC، از قانون القای الکترومغناطیسی فارادی، برای تبدیل یک انرژی مکانیکی مانند دوران به انرژی الکتریکی یک شکل موج سینوسی استفاده میکند. یک ژنراتور ساده، از یک جفت آهنربای دائمی که یک میدان مغناطیسی ثابت را بین دو قطب شمال و جنوب تولید میکند، تشکیل شدهاست. درون این میدان مغناطیسی، یک حلقهی سیم مستطیلی شکل وجود دارد که میتواند به دور یک محور ثابت بچرخد و به آن اجازه میدهد که شار مغناطیسی را در زوایای مختلف قطع کند که در شکل زیر نشان داده شدهاست.
ژنراتور AC تک سیم پیچ ساده
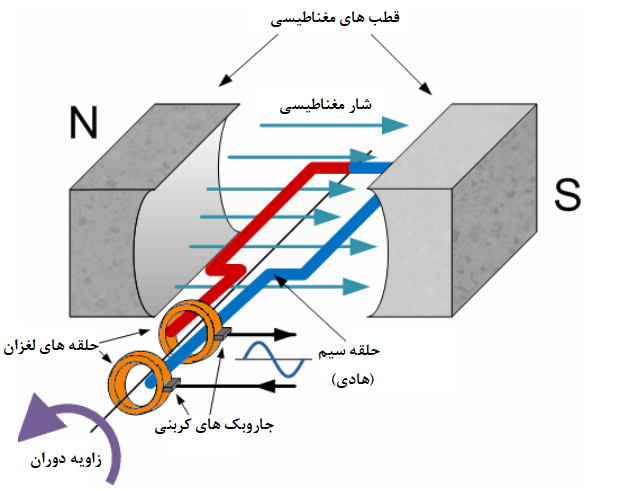 1. ژنراتور AC تک سیم پیچ ساده
1. ژنراتور AC تک سیم پیچ ساده
در حالی که، سیم پیچ در خلاف جهت عقربههای ساعت به دور محور مرکزی، که عمود بر میدان مغناطیسی است میچرخد؛ حلقه سیم خطوط نیروی مغناطیسی تنظیم شده بین قطبهای شمال و جنوب را در زوایای مختلف، هنگام دوران قطع مینماید. مقدار EMF القایی در حلقه، در هر لحظه از زمان متناسب با زاویه دوران حلقه سیم است. با دوران این حلقه سیم، الکترونهای موجود در حلقه سیم در یک جهت به دور حلقه جریان مییابند. در حالی که وقتی حلقه سیم بیشتر از 180° میچرخد و در امتداد خطوط مغناطیسی نیرو حرکت میکند؛ الکترونهای حلقه سیم در جهت مخالف تغییر میکنند و جریان مییابند. پس جهت حرکت الکترون، قطب ولتاژ القایی را تعیین میکند.
بنابراین، میتوان دید که وقتی حلقه یا سیم پیچ به طور فیزیکی یک دور کامل یا ۳۶۰° دوران می یابد؛ یک شکل موج سینوسی کامل با یک سیکل شکل موج تولید شده برای هر دور سیم پیچ تولید میشود. درحالیکه سیم پیچ در داخل میدان مغناطیسی میچرخد؛ اتصالات الکتریکی با استفاده از جاروبکهای کربنی و حلقههای لغزان که برای انتقال جریان الکتریکی القایی کویل استفاده میشوند، به سیم پیچ متصل میگردند.
مقدار EMF القا شده به یک کویل، که خطوط مغناطیسی نیرو را قطع میکند، توسط سه عامل زیر تعیین میشود:
- سرعت: سرعت دوران سیم پیچ در داخل میدان مغناطیسی
- قدرت: قدرت میدان مغناطیسی
- طول: طول سیم پیچ یا هادی که از میدان مغناطیسی عبور میکند.
طبق آنچه در مقالههای گذشته مطرح شده بود؛ فرکانس یک منبع تغذیه، تعداد دفعاتی است که یک سیکل در یک ثانیه ظاهر میشود و برحسب هرتز اندازهگیری میشود. همانگونه که در بالا نشان داده شدهاست؛ با هر دوران کامل سیم پیچ از طریق یک میدان مغناطیسی متشکل از قطب شمال و جنوب، یک چرخه القا شده EMF تولید میشود و اگر کویل با سرعت ثابت دوران یابد، تعداد ثابتی از سیکلها در ثانیه به وجود میآیند که سبب به وجود آمدن فرکانس ثابت میگردند. بنابراین، افزایش سرعت دوران سیم پیچ، سبب افزایش فرکانس گشته و فرکانس متناسب با سرعت دوران است در جایی که N=r.p.m است.
همچنین، ژنراتور تک سیم پیچ ساده ما، تنها دارای دو قطب است، یک قطب شمال و یک قطب جنوب که یک جفت قطب را در اختیار ما قرار میدهد. اگر قطبهای مغناطیسی بیشتری را به ژنراتور بالا اضافه کنیم؛ به طوریکه اکنون در مجموع دارای چهار قطب باشد، دو قطب شمال و دو قطب جنوب، سپس برای هردور سیم پیچ، دو سیکل با همان سرعت دوران تولید میگردد. از این رو فرکانس متناسب با تعداد جفت قطبهای مغناطیسی ژنراتور نیز میباشد در جایی که P برابر با تعداد جفت قطبها میباشد.
در نتیجه با توجه به دو مورد ذکر شده، میتوان گفت که فرکانس خروجی یک ژنراتور AC برابر است با:
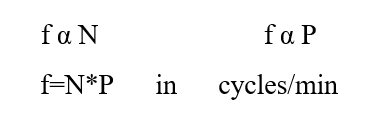
(فرکانس متناسب با N و P بوده و از ضرب آنها در یکدیگر بر حسب سیکل بر دقیقه به دست میآید) در صورتی که بخواهیم فرکانس بر حسب هرتز محاسبه گردد:
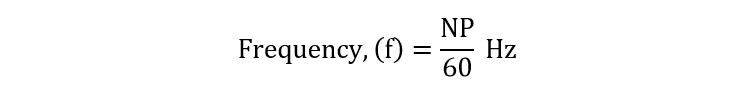
N: سرعت چرخش برحسب r.p.m
P: تعداد جفت قطبها و
۶۰ ضریب تبدیل به ثانیه میباشد.
ولتاژ لحظه ای
EMF القا شده در هر لحظه از زمان در سیم پیچ، به نرخ یا سرعتی که سیم پیچ، خطوط شار مغناطیسی بین قطبها را قطع میکند؛ بستگی دارد و این به زاویه دوران، تتا (θ) دستگاه تولید کننده بستگی دارد. از آن جایی که یک شکل موج AC ، دائما مقدار یا دامنه خود را تغییر میدهد، شکل موج در هر لحظه ای از زمان، مقداری متفاوت از لحظه بعدی خود خواهد داشت. برای مثال مقدار شکل موج در 1ms با مقدار در 1.2ms متفاوت خواهد بود و اینگونه ادامه خواهد یافت. این مقادیر به طور کل، به عنوان مقادیر لحظه ای یا Vi شناخته میشوند. مقدار لحظهای شکل موج و همچنین جهت آن، با توجه به موقعیت کویل در داخل میدان مغناطیسی تغییر میکند. همانگونه که در زیر نشان داده شدهاست.
جابجایی سیم پیچ در یک میدان لحظه ای
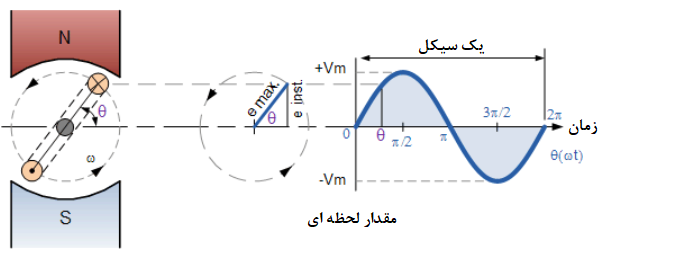 ۲. جابجایی سیم پیچ در یک میدان لحظه ای
۲. جابجایی سیم پیچ در یک میدان لحظه ای
مقادیر لحظه ای یک شکل موج سینوسی به صورت زیر است:
” مقدار لحظه ای = (حداکثر مقدار x ) × (sinθ)”
و فرمول کلی آن به صورت خواهد بود:
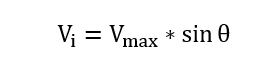
در فرمول بالا، Vmax حداکثر ولتاژ القایی در سیم پیچ است و θ=ωt زاویه دوران کویل با توجه به زمان است.
اگر مقدار حداکثر یا پیک موج را بدانیم؛ با استفاده از فرمول بالا میتوان مقادیر لحظهای را در نقاط مختلف امتداد شکل موج محاسبه کرد. با رسم این مقادیر روی کاغذ گراف میتوان شکل موج سینوسی ساخت. برای سادگی، شکل موج سینوسی را در هر 45° رسم میکنیم که 8 نقطه برای رسم در اختیار ما قرار میدهد. همچنین، دوباره برای سادگی، مقدار حداکثر ولتاژ(Vmax) را 100V در نظر خواهیم گرفت.
رسم مقادیر لحظه ای در فواصل کوتاهتر، به عنوان مثال، در هر ۳۰° (۱۲ نقطه رسم) یا ۱۰° (۳۶ نقطه رسم) میتواند منجر به ساخت شکل موج سینوسی دقیقتر شود.
ساخت شکل موج سینوسی

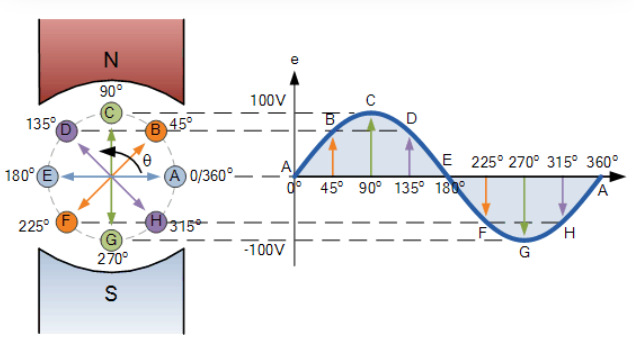 ۳. ساخت شکل موج سینوسی
۳. ساخت شکل موج سینوسی
نقاط بر روی شکل موج سینوسی، با طرح ریزی سراسری از موقعیتهای مختلف دوران بین ۰° تا ۳۶۰° بر مختصات شکل موج که مرتبط با زاویه θ و هنگامی که حلقه سیم یا سیم پیچ یک دور کامل یا ۳۶۰° دوران میکند به دست میآیند و سبب تولید یک شکل موج کامل میشوند.
از نمودار شکل موج سینوسی میتوان دریافت که وقتی که θ برابر با 0°،180° و 360° میباشد، EMF تولید شده، صفر است؛ زیرا سیم پیچ حداقل مقدار خطوط شار را قطع میکند. اما زمانی که θ برابر با 90° و یا 270° میباشد؛ EMF تولید شده حداکثر مقدار خود را به دلیل قطع کردن بیشترین خطوط شار دارد. از این رو، شکل موج سینوسی، یک پیک یا قله مثبت در 90° و یک پیک یا قله منفی در 270° دارد. موقعیت های B،D،F و H مقداری از EMF را با استفاده از فرمول e=Vmax*sinθ تولید میکنند.
فرم شکل موج تولید شده توسط ژنراتور تک حلقه ساده مطرح شده، معمولا به عنوان موج سینوسی شناخته میشود؛ زیرا از نظر شکل، سینوسی است. به این نوع شکل موج، سینوسی گفته میشود؛ زیرا بر اساس تابع سینوسی مثلثاتی است که در ریاضیات (x(t)=Amax.sinθ) استفاده میشود.
هنگام کار با امواج سینوسی در حوزه زمان و به ویژه امواج سینوسی مربوط به جریان، واحد اندازهگیری مورد استفاده در امتداد محور افقی شکل موج، میتواند زمان، درجه و یا رادیان باشد. در مهندسی الکترونیک، معمولا استفاده از رادیان برای اندازهگیری زاویه ای در امتداد محور افقی؛ رایج تر از درجه است. برای مثال ω=100 rad/s یا ω=500 rad/s .
رادیان
یک رادیان (rad) در تعریف ریاضیاتی، به عنوان یک ربع از دایره شناخته میشود؛ که در آن فاصله محیط دایره برابر با طول شعاع (r) همان دایره است. از آنجایی که محیط دایره برابر با شعاع*2π است، باید در اطراف 360° دایره، 2π رادیان باشد.
به بیان دیگر، رادیان واحد اندازهگیری زاویه ای بوده و طول یک رادیان (r) برابر با 6.284 (2*π) بار، اطراف کل دایره خواهد بود و یک رادیان برابر با 360°/2π=57.3° میباشد. در مهندسی الکترونیک، استفاده از رادیان بسیار رایج است. بنابراین یادآوری فرمول زیر حائز اهمیت است:
تعریف یک رادیان
در استفاده از رادیان، به عنوان واحد اندازه گیری شکل موج سینوسی، 2π رادیان برای یک سیکل کامل، برابر با 360° میباشد. از این رو، نیمی از شکل موج سینوسی باید برابر با 1π رادیان یا فقط π(pi) باشد. بنابراین با دانستن اینکه pi(π) برابر با 3.142 میباشد؛ رابطهی میان درجه و رادیان یک شکل موج سینوسی بدین ترتیب خواهد بود:
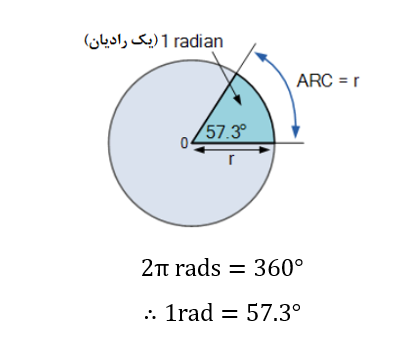 ۴. تعریف یک رادیان
۴. تعریف یک رادیان
ارتباط بین درجه و رادیان
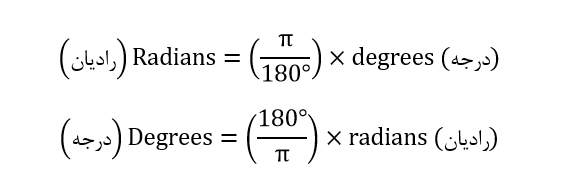
استفاده از این دو معادله در نقاط مختلف در امتداد شکل موج:
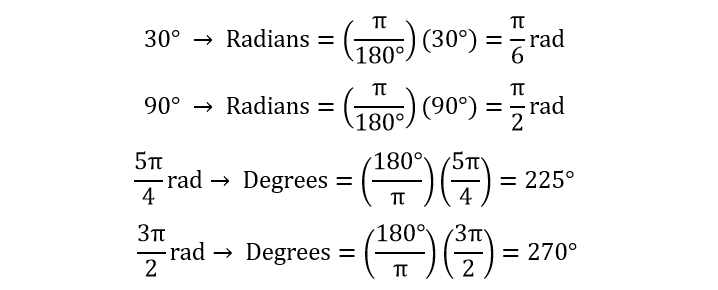
تبدیل بین درجه و رادیان برای معادلهای متداولتری که در تحلیل سینوسی استفاده میشود در جدول زیر آورده شدهاست.
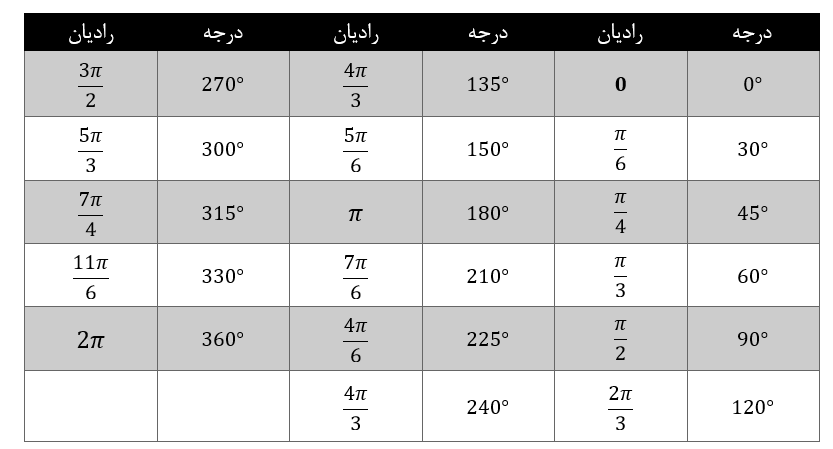
سرعت دوران ژنراتور به دور محور مرکزی خود، فرکانس شکل موج سینوسی را تعیین میکند. همانطور که شکل موج، دارای فرکانس (f) برحسب هرتز یا سیکل بر ثانیه است؛ دارای فرکانس زاویهای(ω) (حرف یونانی امگا) برحسب رادیان بر ثانیه نیز میباشد. سرعت زاویه ای شکل موج سینوسی به صورت زیر محاسبه میگردد:
سرعت زاویه ای یک شکل موج سینوسی
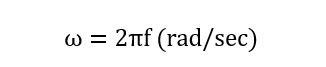
در انگلستان، سرعت یا فرکانس زاویهای منبع تغذیه به صورت زیر به دست میآید:
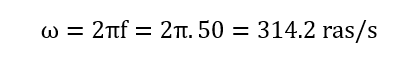
در آمریکا، به دلیل اینکه فرکانس منبع تغذیه برابر با 60Hz است، مقدار بدست آمده در بالا برابر با 377 rad/s است.
بنابراین، اکنون میدانیم، که سرعت دوران ژنراتور به دور محور مرکزی خود؛ فرکانس شکل موج سینوسی را تعیین میکند و میتوان آن را سرعت زاویهای(ω) نیز نامید و نیز تا کنون باید بدانیم که زمان لازم برای انجام یک سیکل کامل برابر با دوره تناوب(T) شکل موج سینوسی است. از آنجایی که فرکانس به صورت معکوس با دوره تناوب متناسب است(f=1/T) میتوانیم مقدار فرکانس موجود در معادله بالا را با دوره تناوب معادل آن جایگزین نمود و در صورت جایگزینی داریم:
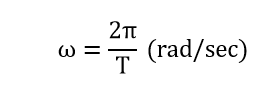
معادله بالا بیان میکند، با کاهش دوره تناوب شکل موج سینوسی، سرعت زاویه ای شکل موج افزایش می یابد و نیز افزایش فرکانس، سبب افزایش سرعت زاویه ای میگردد.
مثال ۱
یک شکل موج سینوسی به صورت تعریف میشود:
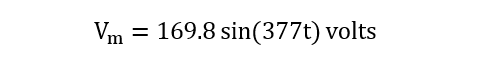
ولتاژ RMS شکل موج، فرکانس آن، ولتاژ لحظه ای(Vi) را پس از گذشت 6ms (6 میلی ثانیه) محاسبه نمایید.
از بالا میدانیم که بیان کلی شکل موج سینوسی عبارت است از:
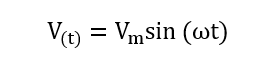
سپس با مقایسه فرمول بالا با آنچه در صورت سوال آورده شدهاست در مییابیم، مقدار پیک ولتاژ ۱۶۹.۸ ولت برای شکل موج است.
شکل موج ولتاژ RMS به صورت زیر محاسبه میشود:
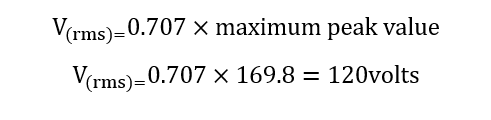
سرعت زاویهای(ω) برابر با 377rad/s یعنی 2πf=377 است. بنابراین فرکانس شکل موج به صورت زیر محاسبه میگردد:
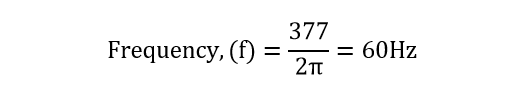
ولتاژ لحظه ای(Vi) پس از 6 میلی ثانیه به صورت زیر محاسبه میگردد:

باید توجه داشت که سرعت زاویه ای در زمان t=6ms برحسب رادیان به دست میآید. در صورت تمایل، میتوان این مقدار را به معادل آن بر حسب درجه تبدیل نمود و از این مقدار برای محاسبه مقدار ولتاژ لحظه ای استفاده کرد. بنابراین، زاویه بر حسب درجه برای ولتاژ لحظه ای به صورت زیر است:
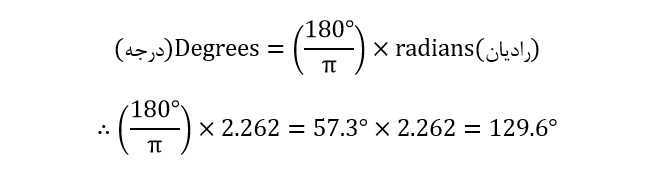
شکل موج سینوسی
سپس قالب کلی مورد استفاده برای تجزیه، تحلیل و محاسبه مقادیر مختلف شکل موج سینوسی به شرح زیر است:
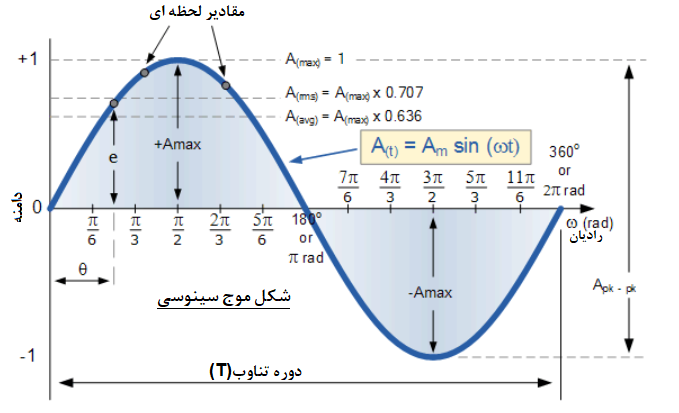 ۵. شکل موج سینوسی
۵. شکل موج سینوسی
در مقاله بعدی، به بررسی تفاوت فازی بین دو شکل موج سینوسی خواهیم پرداخت؛ بدین صورت که این شکل موجها دارای فرکانس یکسان بوده اما در فواصل زمانی مختلف از محور افقی صفر عبور میکنند.


دیدگاه خود را بنویسید