تبدیلات ستاره و دلتا

تبدیلات ستاره-دلتا و تبدیلات دلتا-ستاره، به ما اجازه می‌دهند تا امپدانس‌های متصل‌شده به یکدیگر را، در پیکربندی‌های ۳ فاز، از یک نوع به نوع دیگر تبدیل کنیم.

اکنون می‌توانیم شبکه‌های مقاومتی ساده سری، موازی یا نوع پل را، با استفاده از روش‌های قوانین مداری کیرشهف، آنالیز جریان مش یا آنالیز ولتاژ گره، حل‌کنیم. اما در یک مدار متوازن سه فاز، می‌توانیم از روش‌های متفاوت ریاضی برای ساده‌سازی تجزیه و‌ تحلیل مدار و بنابراین کاهش محاسبات ریاضی درگیر، استفاده کنیم؛ که به خودی خود چیز خوبی است.

مدارها یا شبکه‌های استاندارد سه فاز، دو شکل با نام‌هایی که نشان‌دهنده‌ی نحوه اتصال رزیستانس‌ها به‌ یکدیگر است، دارند؛ شبکه‌ی اتصال ستاره، که دارای نماد حرف Y (وای) بوده و شبکه‌های اتصال دلتا، که دارای نماد مثلث ∆ (دلتا) است.

اگر یک منبع سه فاز، سه سیمه یا حتی یک بارِ ۳فاز، در یکی از این پیکربندی‌ها متصل شده‌باشد، می‌توان به‌سادگی، تبدیل یا تغییر به یک پیکربندی معادل نوع دیگر خود، با استفاده از روش تبدیل ستاره-دلتا یا تبدیل دلتا-ستاره، داشته‌باشد.

یک شبکه‌ی مقاومتی تشکیل‌شده از سه امپدانس، می‌تواند به شکل پیکربندی T یا “تی” باشد؛ اما می‌توان آن را به نوع شبکه‌ی ستاره یا Y به‌صورت زیر، تبدیل‌کرد.

اتصال T و معادل شبکه‌ی ستاره

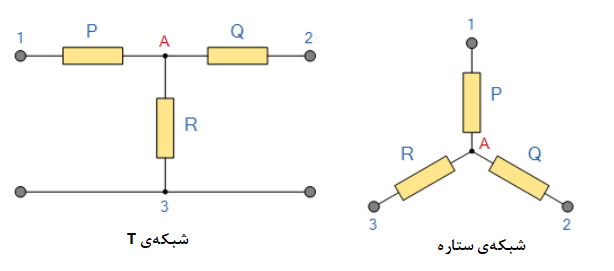
همانطور که تا الان مشاهده نمودیم؛ می‌توانیم یک شبکه‌ی مقاومت T را در بالا برای تولید شبکه‌ی معادل الکتریکی نوع ستاره یا Y ترسیم‌ کنیم. اما همچنین می‌توانیم تبدیل شبکه‌ی مقاومتی نوع Pi یا π را نیز، به‌ معادل الکتریکی نوع دلتا یا ∆، به‌صورت زیر نمایش دهیم.

اتصال Pi و معادل شبکه‌ی دلتا

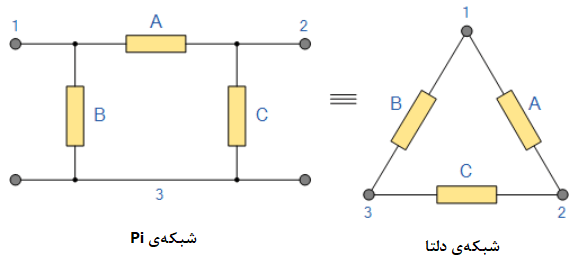
با تعریف دقیق شبکه‌ی اتصال ستاره یا دلتا، تبدیل Y به مدار معادل ∆ و نیز تبدیل ∆ به مدار معادل Y، با استفاده از روش‌های تبدیل امکان‌پذیر است. این روش به ما اجازه‌ی تولید رابطه‌ی ریاضیاتی بین مقاومت‌های مختلف، با استفاده از تبدیل ستاره-دلتا به‌همراه تبدیل دلتا-ستاره را می‌دهد.

این تبدیلات مدار، به ما اجازه‌ی تغییر سه مقاومت متصل (یا امپدانس) را به معادل‌های آن‌ها که بین پایانه‌های ۱-۲،۱-۳ و ۲-۳ برای مدار اتصال ستاره یا دلتا، اندازه‌گیری شده‌است، می‌دهد. با این حال شبکه‌های به‌دست‌آمده، تنها برای ولتاژها و جریان‌های خارج از شبکه‌ی ستاره یا دلتا معادل بوده، زیرا ولتاژها و جریان‌های داخلی متفاوت می‌باشند؛ اما هر شبکه، مقدار یکسانی از توان را مصرف کرده و ضریب توان یکسانی برای یکدیگر دارند.

تبدیل دلتا ستاره

برای تبدیل یک شبکه‌ی دلتا به شبکه‌ی ستاره‌ی معادل آن، باید یک فرمول تبدیل برای برابر نمودن مقاومت‌های مختلف با یکدیگر بین پایانه‌های مختلف، به‌دست آوریم. مدار زیر را در نظر بگیرید.

شبکه‌ی دلتا به ستاره

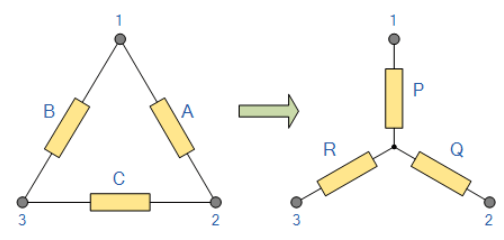شماتیک تبدیل دلتا ستاره

رزیستانس های بین پایانه‌های ۱ و ۲ را مقایسه کنید.

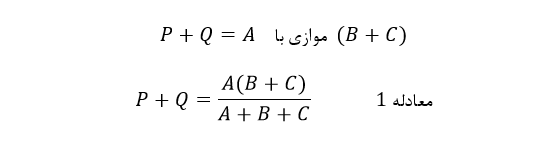
رزیستانس بین پایانه‌های ۲ و ۳.

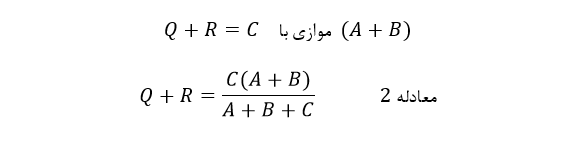
رزیستنس بین پایانه‌های ۱ و ۳.

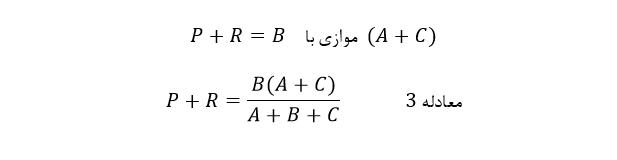
این عمل، به ما سه معادله را خواهد داد و با کم‌کردن معادله‌ی ۲ از ۳، خواهیم‌داشت:

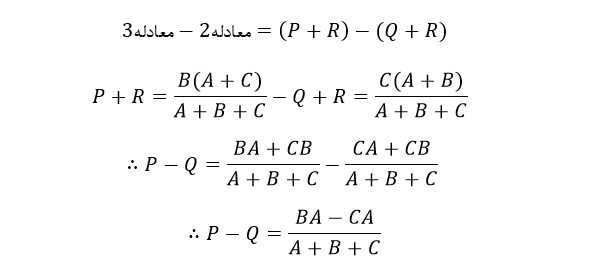
سپس با نوشتن دوباره‌ی معادله ۱، خواهیم داشت:

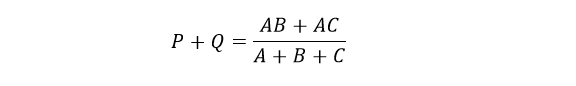
با جمع معادله‌ی ۱ با نتیجه‌ی تفریق معادله‌ی ۳ از ۲ ، خواهیم داشت:

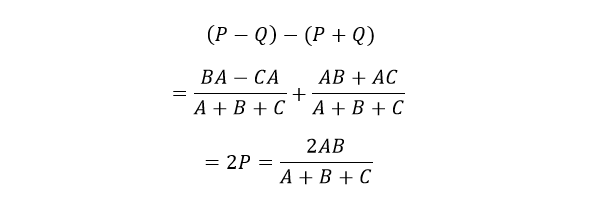
که از آن معادله‌ی نهایی، مقاومت P خواهدبود:

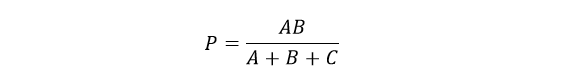
سپس برای خلاصه کردن ریاضیات بالا، می‌توانیم بگوییم که مقاومت P در شبکه‌ی ستاره، می‌تواند با جمع معادله‌ی 1 با (تفریق معادله‌ی 2 از 3) یا ((معادله‌ی 2–معادله‌ی ۳) + معادله‌ی۱ ) به‌دست آید.

به‌طورمشابه، برای یافتن مقاومت Q در شبکه‌ی ستاره، می‌توان، آن را، با جمع معادله‌ی 2 با (تفریق معادله‌ی 3 از 1) یا ((معادله‌ی 3–معادله‌ی 1) + معادله‌ی2 ) به‌دست آورد؛ که به ما تبدیل Q را به‌صورت زیر می‌دهد:

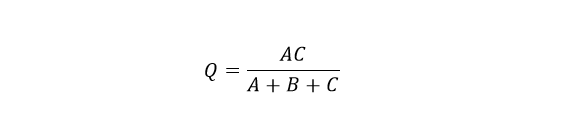
و نیز دوباره، برای یافتن مقاومت R در شبکه‌ی ستاره، می‌توان، آن را، با جمع معادله‌ی 3 با (تفریق معادله‌ی 1 از 2) یا ((معادله‌ی 1–معادله‌ی 2)+معادله‌ی3 ) به‌دست آورد؛ که به ما تبدیل R را به‌صورت زیر می‌دهد:

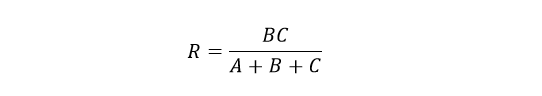
هنگام تبدیل شبکه‌ی دلتا به شبکه‌ی ستاره، مخرج تمام فرمول‌های تبدیل یکسان و برابر با A+B+C بوده، که مجموع تمام رزیستانس‌های دلتا است. پس برای تبدیل هر شبکه‌ی اتصال دلتا به معادل شبکه‌ی ستاره‌ی آن، می‌توانیم معادلات تبدیل بالا را به‌صورت زیر خلاصه کنیم:

معادلات تبدیلات دلتا به ستاره

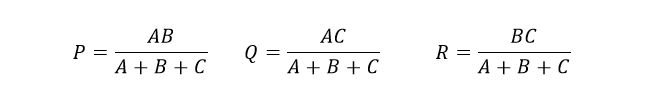
اگر سه مقاومت در شبکه‌ی دلتا، از نظر مقدار باهم برابر باشند؛ مقاومت‌های به‌دست‌آمده در شبکه‌ی ستاره‌ی معادل آن، برابر با یک سوم مقدار مقاومت‌های دلتا است. این امر به هر مقاومت شاخه در شبکه‌ی ستاره مقدار Rستاره = 1/3*Rدلتا  را می‌دهد که همچنین می‌توان گفت: (Rدلتا)/۳.

مثال ۱

شبکه‌ی مقاومتی دلتا در زیر را به شبکه‌ی ستاره‌ی معادل آن، تبدیل‌کنید.

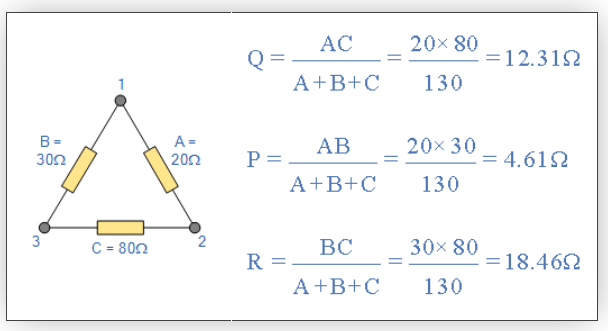حل مثال ۱

تبدیل ستاره-دلتا

تبدیل ستاره-دلتا، به‌سادگی معکوس بالا می‌باشد. دیدیم که هنگام تبدیل شبکه‌ی دلتا به شبکه‌ی ستاره‌ی معادل آن، مقاومت متصل‌شده به یک پایانه، حاصل‌ضرب دو رزیستانس دلتای‌ متصل‌شده به همان پایانه است. برای مثال، مقاومت P، حاصل‌ضرب مقاومت‌های A و B متصل‌شده به پایانه‌ی 1 است.

با دوباره نوشتن کمی از معادلات قبلی، می‌توان معادلات تبدیل را برای تبدیل شبکه‌ی مقاومتی ستاره به شبکه‌ی دلتای معادل آن پیدانمود؛ که به ما راه ایجاد تبدیل ستاره- دلتا را به‌صورت زیر می‌دهد.

تبدیل ستاره به دلتا

مقدار مقاومت در هر طرف شبکه‌ی دلتا ∆ برابر با مجموع حاصل‌ضرب‌های ترکیب دو مقاومت در شبکه‌ی ستاره، تقسیم بر مقاومت ستاره‌ی “مستقیما مقابل” آن بوده و مقاومت دلتا پیدا می‌شود. برای مثال مقاومت A خواهد بود:

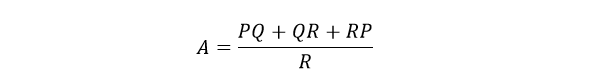
با توجه به پایانه‌ی 3 و مقاومت B خواهیم داشت:

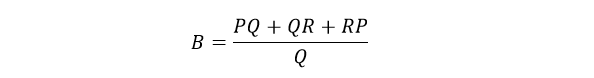
با توجه به پایانه‌ی 2 و مقاومت C خواهیم داشت:

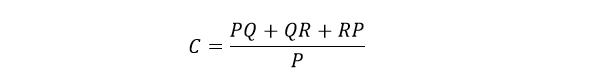
با توجه به پایانه‌ی ۱ داریم.

با تقسیم هر معادله بر مقدار مخرج، سه فرمول تبدیل جداگانه به‌دست می‌آید؛ که می‌توان از آن‌ها برای تبدیل هر شبکه‌ی مقاومتی دلتا به شبکه‌ی ستاره‌ی معادل آن، استفاده کرد.

معادلات تبدیل ستاره-دلتا

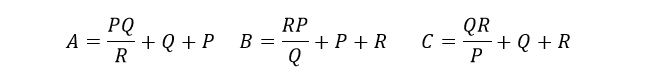
آخرین نکته برای تبدیل شبکه‌ی مقاومتی ستاره به شبکه دلتای معادل آن این است که، اگر تمام مقاومت‌ها در شبکه‌ی ستاره از نظر مقداری برابر باشند، مقاومت‌های به‌دست‌آمده در شبکه‌ی معادل دلتا، برابر با سه برابر مقدار مقاومت‌های شبکه‌ی ستاره بوده و به ما Rدلتا = 3*Rستاره را خواهد داد.

مثال ۲

شبکه‌ی مقاومتی ستاره در زیر را به شبکه‌ی دلتای معادل آن، تبدیل‌کنید.

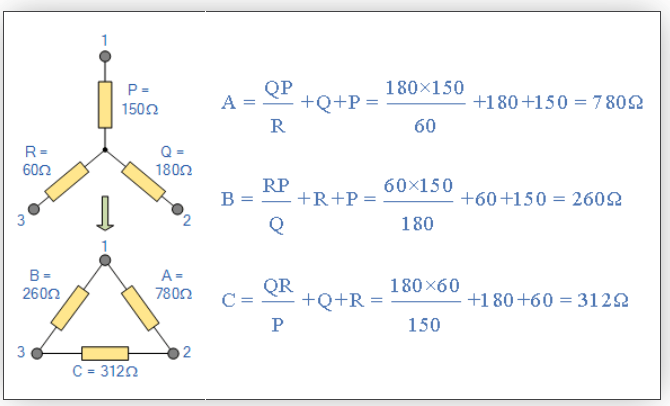حل مثال ۲

هر دو تبدیل ستاره-دلتا و تبدیل دلتا-ستاره، به ما اجازه‌ می‌دهند تا یک نوع از اتصال مدار را به نوع دیگر، برای آسان‌تر شدن آنالیز مدار تبدیل کنیم. این روش‌های تبدیل، می‌توانند بر روی مدارهای ستاره یا دلتای حاوی رزیستانس یا امپدانس اثر خوبی داشته‌باشند.