ثابت زمانی تاو

تاو، ثابت زمانی یک مدار RC است؛ که زمانی‌که تحت شرایط ورودی تغییر پله قرار می‌گیرد؛ از یک شرایط حالت پایدار به حالت پایدار دیگری تغییر می‌کند.

تاو، با نماد τ، حرف یونانی است؛ که در محاسبات الکتریکی و الکترونیکی برای نشان‌دادن ثابت زمانی یک مدار به‌عنوان تابعی از زمان استفاده می‌شود. اما منظور ما از پاسخ گذرا و ثابت زمانی مدارها چیست؟!

مدارهای الکتریکی و الکترونیکی همیشه در وضعیت با ثبات یا پایدار نیستند و می‌توانند در معرض تغییرات ناگهانی پله‌ای به‌شکل تغییر سطوح ولتاژ یا شرایط ورودی، قرار گیرند. به‌عنوان مثال، باز و بسته‌کردن کلید یا سنسور ورودی.

با این‌حال، هر زمان که یک تغییر ولتاژ یا حالت رخ دهد؛ مدار ممکن است فورا به این تغییر واکنش ندهد و مقداری زمان صرف شود؛ صرف‌نظر از اینکه قطعات راکتیو مانند خازن و سلف در مدار وجود داشته باشد.

تغییر حالت از یک شرایط پایدار به حالت دیگر، معمولا با نرخی که توسط ثابت زمانی مدار تعیین می‌شود؛ اتفاق می‌افتد که خود یک مقدار نمایی خواهد بود. پس ثابت زمانی یک مدار مشخص می‌کند؛ که چگونه پاسخ گذرا جریان و ولتاژ مدارها در یک دوره زمانی مشخص تغییر می‌کند.

 در اتصال به یک ولتاژ DC حالت مانا، یک خازن مانند یک مدار باز، یک سلف همانند یک اتصال کوتاه و یک مقاومت به‌عنوان یک وسیله‌ی محدودکننده‌ی جریان، عمل می‌کند. اگر ولتاژ دوسر خازن و هم‌چنین جریان عبوری از یک سلف، ‌نتوانند فورا تغییر کنند؛ در این‌صورت وقتی تحت تاثیر شرایط تغییر پله، قرار می‌گیرند؛ پاسخ گذرا آنها چگونه خواهدبود؟!

قبل از اینکه شروع به اعمال نوعی تحلیل گذرا به مدار خازنی کنیم؛ ابتدا مشخصه‌های V-I یک مدار مقاومتی معمولی را همانطور که در زیر نشان داده شده‌است؛ یادآوری می‌کنیم.

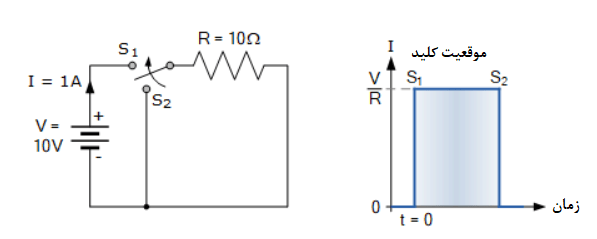
زمانی‌که، سوئیچ در موقعیت S۲ قرار دارد؛ مقاومت 10 اهم، اتصال کوتاه شده و از این‌رو، به منبع ولتاژ 10 ولت، وصل نمی‌شود. درنتیجه، جریان صفر در مقاومت،IR=0 شارش می‌یابد. اما وقتی سوئیچ در موقعیت S۱ در زمان t=0 قرار دارد؛ یک ولتاژ پله‌ای 10 ولت، مستقیما به دو سر مقاومت 10 اهم اعمال می‌شود؛ درنتیجه، جریان 1 آمپر(I=V/R) در مدار بسته، شارش می‌یابد.

از آنجایی‌که مقاومت، مقدار غیرالقایی و ثابتی دارد؛ به محض اینکه سوئیچ به موقعیت S۱ منتقل شود؛ جریان بلافاصله از 0 به 1 آمپر در کسری از ثانیه، تغییر می‌کند. به‌همین ترتیب، اگر کلید به موقعیت S۲ برگردد؛ ولتاژ تغذیه(V) حذف می‌شود؛ بنابراین جریان مدار بلافاصله دوباره به صفر می‌رسد؛ همانطور که در نمودار بالا نشان داده شده‌است.

پس برای یک مدار مقاومتی، تغییر حالت الکتریکی از یکی به دیگری، تقریبا سریع است؛ زیرا چیزی برای مقاومت در برابر این تغییر، وجود ندارد. پس، مقاومت‌ها، فقط جریان الکتریکی را در اطراف مدار، با مقداری که توسط قانون اهم تعیین می‌شود؛ یعنی V/R محدود می‌کنند و به این ترتیب، هیچ ثابت زمانی یا پاسخ گذرایی مرتبط با آن‌ها وجود ندارد.

حال بیایید؛ پاسخ گذرای یک مقاومت را که به‌صورت سری به خازن متصل شده‌است؛ در نظر بگیریم؛ که یک مدار RC ساده را تشکیل می‌دهد. مشخصه‌های V-I این ترکیب، زمانی که همانند قبل در معرض تغییر ولتاژ پله ورودی، قرار می‌گیرد؛ چه خواهدبود؟!

ثابت زمانی RC

در بالا دیدیم؛ که یک مقاومت، فورا به هر تغییری در ولتاژ اعمالی به آن، پاسخ می‌دهد. اما مقاومت، یک قطعه‌ی خطی پسیو است؛ که انرژی را ذخیره نمی‌کند؛ بلکه انرژی را به شکل گرما تلف می‌کند. اما یک خازن (C) از دو صفحه‌ی رسانا (الکترود) تشکیل شده‌است؛ که توسط یک ماده‌ی عایق دی‌الکتریکی از هم جدا شده‌اند و توانایی ذخیره‌ی انرژی الکتریکی به شکل بار الکترواستاتیکی (Q کولمب) را درون خود دارد.

نتیجه این است؛ که برخلاف مقاومت، خازن نمی‌تواند فورا به تغییرات سریع یا پله‌ای ولتاژ اعمالی واکنش نشان دهد. بنابراین، همیشه بلافاصله پس از اعمال ولتاژ، مدت زمان کوتاهی وجود دارد؛ تا جریان مدار و ولتاژ دو سر خازن، تغییر حالت دهند. به عبارت دیگر، مدت زمان مشخصی برای خازن، لازم است؛ تا مقدار انرژی ذخیره‌شده در میدان الکتریکی خود را تغییر دهد؛ چه مقدار آن افزایش یا کاهش یابد.

مقدار زمان لازم برای مدار که به پاسخ برسد؛ برابر با حاصل‌ضرب R x C است؛ یعنی حاصل‌ضرب “اهم x فاراد” ، برحسب ثانیه (s) خواهدبود. شارش جریان در خازن به‌صورت iC=C(dv/dt) خواهدبود؛ که در آن dv نشان‌دهنده‌ی تغییر ولتاژ و dt نشان‌دهنده‌ی تغییر زمان است.

مدار ساده‌ی مقاومت – خازن RC زیر را درنظر بگیرید.

مدار مقاومت - خازنی (RC)

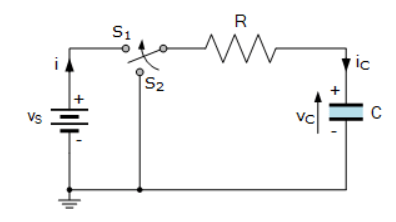
وقتی سوئیچ، برای مدتی در موقعیت S۲ قرار دارد؛ ترکیب مقاومت – خازن، اتصال کوتاه شده و بنابراین، به منبع تغذیه‌، VS وصل نیست. درنتیجه، شارش جریان در مدار 0 است؛ پس I=0 و VC=۰ است.

هنگامی‌که، کلید به موقعیت S۱ در زمان t=0 منتقل می‌شود؛ یک ولتاژ پله (V) به مدار RC اعمال می‌شود. در این لحظه از زمان، خازن کاملا از شارژ تخلیه شده و مانند یک اتصال کوتاه رفتار می‌کند؛ که دلیل آن تغییر وضعیت ناگهانی dv/dt، دقیقا لحظه‌ای است؛ که کلید در موقعیت S۱ بسته می‌شود.

این تغییر باعث می‌شود؛ که جریان مدار، به‌ مقداری که فقط با مقاومت مدار محدود می‌شود؛ مانند قبل افزایش یابد. بنابراین، هنگامی‌که، کلید S۱ در ابتدا و در t=0 بسته می‌شود؛ جریانی که در مدار بسته می‌گذرد؛ تقریبا برابر با VR/R برحسب آمپر است؛ از آنجایی‌که، VR=I*R و VC=۰ است.

در همان لحظه‌ای که سوئیچ به موقعیت S۱ منتقل می‌شود و همچنین جریان در مدار شارش می‌کند؛ خازن تخلیه‌شده، شروع به شارژشدن می‌کند؛ زیرا تلاش می‌کند؛ بار الکتریکی را روی صفحات خود ذخیره کند. نتیجه این است؛ که ولتاژ VC در دوسر خازن، به‌تدریج شروع به افزایش می‌کند؛ درحالی‌که، جریان مدار با نرخی که توسط ثابت زمانی، تاو ترکیب RC تعیین می‌شود؛ شروع به کاهش می‌کند.

بنابراین، می‌توانیم رشد ولتاژ را در صفحات خازن (VC) با شروع از t=0 ، به‌صورت زیر تعریف کنیم:

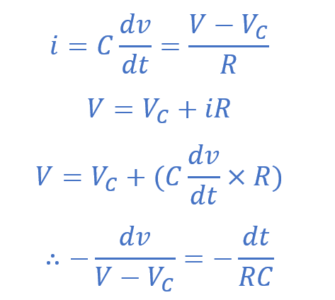
انتگرال‌گرفتن از دو طرف به ما می‌دهد:

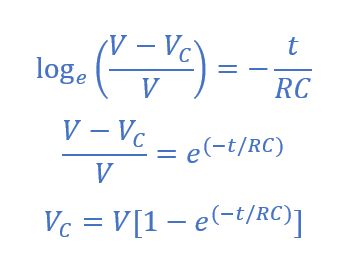
بنابراین، رشد طبیعی نمایی ولتاژ دوسر خازن، درحالی‌که، تلاش می‌کند؛ بار را روی صفحات خود ذخیره کند؛ به‌صورت زیر است:

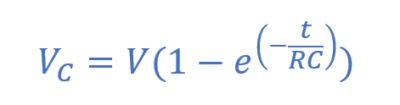
در فرمول بالا:

VC، برابر با ولتاژ دوسر خازن است.

V برابر با منبع ولتاژ است.

e برابر با پایه‌ی لگاریتم طبیعی است.

t دوره زمانی از بسته‌شدن سوئیچ است.

RC، ثابت زمانی تاو از مدار RC است.

می‌توانیم نرخ رشد نمایی ولتاژ در خازن را در طول زمان، در جدول زیر، با فرض مقادیر نرمال‌شده برای ولتاژ تغذیه‌ی 1 ولت و ثابت زمانی RC، یک (1)  نشان دهیم.

رشد ولتاژ خازن در طول زمان

زمان (ثانیه)

۰.۵

۰.۷

۱

۲

۳

۴

۵

۶

مشخصا از جدول بالا، می‌توانیم ببینیم که مقادیر VC=V(1-e-t/T) در مثال ما، با گذشت زمان از t=0 به t=6 ثانیه (6T)، افزایش می‌یابد و ولتاژ دو سر خازن، یک تابع نمایی افزایشی است؛ زیرا با گذشتن زمان (t)، عبارت e-t/T کوچک و کوچکتر می‌شود و بنابراین، ولتاژ در خازن VC نسبت به ولتاژ منبع تغذیه، بزرگتر می‌شود.

پس، در زمان t=0، مقدار تابع صفر است؛ اما با افزایش زمان (t) به سمت ∞، نقطه‌ای که در آن t=RC در زمان 1-e-۱ است؛ ارزش ۰.۶۳۲ یا ۶۳.۲%(۰.۶۳۲*۱۰۰%) مقدار نهایی حالت مانا را تولید می‌کند.

از این‌رو، برای یک تابع افزایشی نمایی، ثابت زمانی تاو (τ) به‌عنوان زمانی تعریف می‌شود؛ که تابع به 63.2% از مقدار حالت مانای نهایی خود با نرخی که از زمان t=0 شروع می‌شود؛ برسد. بنابراین، در هر بازه‌ی زمانی از تاو (τ)، ولتاژ دو سر خازن، با اندازه‌ی e-۱ مقدار قبلی آن، افزایش می‌یابد و هرچه ثابت زمانی تاو، کوچکتر باشد؛ سرعت تغییر سریع‌تر است.

می‌توانیم تغییرات (variation) ولتاژ خازن را نسبت به زمان، به‌صورت گرافیکی در زیر نشان دهیم:

رشد ولتاژ نمایی در طول زمان

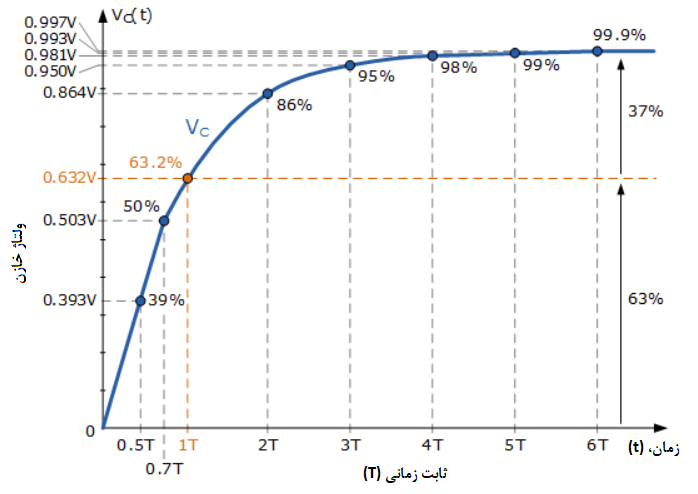
پس می‌توانیم ببینیم؛ که پاسخ گذرای یک خازن به یک ورودی پله، آنی یا خطی نیست؛ بلکه به صورت نمایی با نرخی که توسط ثابت زمانی مدار RC تعیین می‌شود؛ افزایش می‌یابد و آن یک ثابت زمانی برابر با یک فاکتور از 1-e-۱=۰.۶۳۲۱ است.

تاو، به خودی خود، توضیح نمی‌دهد؛ که چه مدت طول می‌کشد؛ تا خازن کاملا شارژ شود و از نظر تئوری، به‌دلیل افزایش نمایی منحنی گذرا، خازن هرگز ۱۰۰% شارژ کامل نمی‌شود.

با این‌حال، پس از یک پریود زمانی برابر یا بزرگتر از معادل 5 ثابت زمانی، یعنی  یا 5RC، از زمانی‌که تغییر اولیه در شرایط رخ داد؛ رشد نمایی به کمتر از 1% از مقدار حداکثر خود کاهش یافته‌است. پس برای بیشتر کاربردهای عملی، می‌توان گفت؛ که به حالت نهایی یا حالت پایدار خود رسیده‌است؛ بدون اینکه با گذشت زمان، تغییر بیشتری صورت گیرد. یعنی در 5T خازن، “شارژ کامل” است.

مثال شماره‌ی ۱ تاو

یک مدار سری RC، دارای مقدار مقاومتی 50 اهم و ظرفیت خازنی 160 میکروفاراد است. ثابت زمانی تاو، این مدار چیست و چقدر طول می‌کشد؛ تا خازن کاملا شارژ شود؟

1. ثابت زمانی تاو برابر با ᴛ=RC است؛ بنابراین:

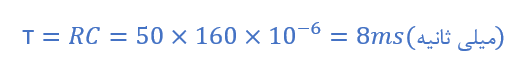
۲. مدت زمان برای شارژ کامل:

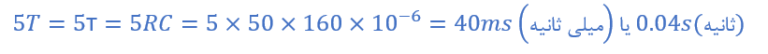
مثال شماره‌ی ۲ تاو

یک مدار، از یک مقدار مقاومتی ۴۰ اهم و ظرفیت خازنی ۳۵۰ میکروفاراد تشکیل‌شده‌است؛ که در حالت سری نسبت به هم قرار گرفته‌اند. اگر خازن کاملا از شارژ تخلیه شود؛ مدت زمانی که طول می‌کشد؛ تا ولتاژ در صفحات خازن به ۴۵% از مقدار نهایی حالت پایدار خود پس از شروع شارژشدن برسد؛ چقدر خواهد بود؟

داده‌هایی که داریم: R=40Ω و C=350uF است و t زمانی‌است؛ که ولتاژ خازن به 45% مقدار نهایی خود می‌رسد؛ که برابر با 0.45V است.

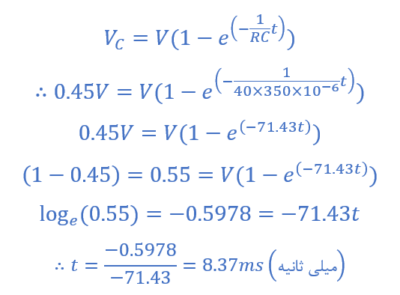
پس، 8.37 میلی‌ثانیه طول می‌کشد؛ تا ولتاژ دوسر خازن به 45% از شرط حالت مانای 5Tخود زمانی‌که ثابت زمانی، تاو برابر با 14 میلی‌ثانیه و 5T برابر با 70 میلی‌ثانیه است؛ برسد.

تا الان باید درک کرده‌باشیم؛ که ثابت زمانی یک مدار RC سری، بازه‌ی زمانی برابر با 0.632 ولت ( معمولا 63.2%) از مقدار حداکثر (V) در انتهای یک ثابت زمانی (1T) است و نتیجه‌، حاصل‌ضرب R و C می‌باشد. همچنین، نماد ثابت زمانی، τ ( حرف یونانی تاو) بوده و ᴛ=RC درجایی است؛ که R برحسب اهم و C برحسب فاراد و τ برحسب ثانیه است.

اما در مورد یک خازن، که کاملا شارژ شده‌است(VC>5T)، ویژگی‌های V-I خازن، زمانی که تخیله شارژ تا صفر صورت می‌گیرد؛ چگونه است و آیا افت ولتاژ خازن از همان شکل منحنی نمایی پیروی می‌کند؟

منحنی تخلیه‌ی شارژ گذرای RC

تخلیه‌ی شارژ یک خازن کاملا شارژشده، مشابه فرآیند شارژشدن است. منبع تغذیه‌ی DC مورداستفاده برای شارژ خازن، در ابتدا قطع‌شده و مطابق شکل با یک اتصال کوتاه، جایگزین می‌شود.

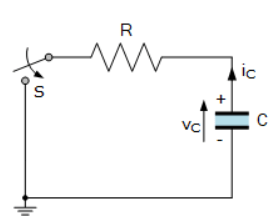
با فرض اینکه، شرایط اولیه به این گونه است؛ که کلید(S) “باز” است و خازن کاملا شارژشده است(VC>5T). زمانی‌که، سوئیچ(S) در زمان t=0 بسته می‌شود؛ خازن شروع به تخلیه از طریق مقاومت کرده و زمان لازم برای تخلیه وابسته به ارزش مقاومت است. از آنجایی‌که، در ابتدا VC=VR=V است؛ افت ولتاژ به‌صورت زیر خواهدبود:

معادله‌ی افت نمایی ولتاژ

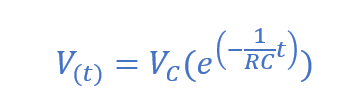
در این معادله، V(t)، ولتاژ دو سر صفحات خازن است و VC، ارزش اولیه‌ی ولتاژ خازن پیش از شروع‌شدن افت است.

پیش از این، تابع نمایی برای رشد ولتاژ بود. برای یک تابع افت ولتاژ به‌صورت نمایی، زمان لازم برای رسیدن ولتاژ به صفر ولت، با نرخ ثابت، همچنان به ثابت زمانی RC بستگی دارد. بنابراین، ثابت زمانی معیاری برای “نرخ افت‌کردن” است.

بنابراین، برای یک تابع افت نمایی، ثابت زمانی تاو (ᴛ) نیز به‌عنوان زمان موردنیاز برای رسیدن ولتاژ افت به حدود 36.8% از مقدار پایدار نهایی خود، در زمانی‌که افت در t=0 شروع می‌شود؛ تعریف می‌شود. بنابراین، اگر ᴛ یک ثابت زمانی باشد یعنی، ᴛ=RC است؛ مدار RC در شرط حالت مانای شارژ کامل خود در t=0 خواهد بود و پس:

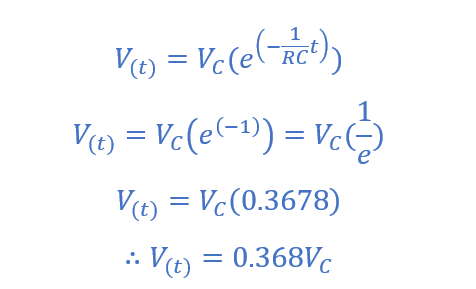
 از این‌رو، در زمان t=0، ارزش تابع در حداکثر خود است؛ اما با حرکت زمان (t) به سمت ∞ ، نقطه‌ای که در آن t=RC است، در زمان e-۱ مقدار ۰.۳۶۸ یا ۳۶.۸% (۰.۳۶۸*۱۰۰) ارزش حالت مانای نهایی را تولید می‌کند؛ که برابر با صفر ولت (تخلیه‌ی کامل) است.

مجددا می‌توانیم نرخ نمایی افت ولتاژ در خازن را در طول زمان، در جدول زیر با مقادیر نرمال‌شده برای ولتاژ تغذیه‌ی 1 ولت و ثابت زمانی RC، 1 نشان دهیم.

افت ولتاژ خازن در طول زمان

زمان (ثانیه)

۰.۵

۰.۷

۱

۲

۳

۴

۵

۶

یک نکته قابل توجه در اینجا، این است؛ که ثابت زمانی تاو، یک مدار RC سری، از مقدار اولیه آن در t=0 تا ᴛ همیشه 63.2% خواهدبود؛ چه خازن در حال شارژ یا تخلیه شارژ باشد. برای رشد نمایی، شرایط اولیه، 0 ولت (0V) است؛ زیرا خازن کاملا تخلیه شده‌است.

بنابراین، رشد نمایی ولتاژ تا 63.2% از VMAX در یک ثابت زمانی، 1T است. اما می‌توانیم همچنین می‌توانیم ولتاژ خازن در 1T را 36.8% از مقدار حالت پایدار نهایی آن در 5T در نظر بگیریم؛ که کاملا شارژ شده‌است.

این ایده، برای افت نمایی نیز صادق است. برای یک خازن کاملا شارژشده، شرایط حالت پایدار اولیه VC(max) است؛ بنابراین، خازن تا 36.8% از حالت پایدار نهایی خود یعنی صفر ولت (0V) پس از 5t تخلیه می‌شود. اما دوباره، می‌توانیم ولتاژ دو سر خازن را در زمان 1T نیز در نظر بگیریم؛ که 63.2% نسبت به شروع اولیه‌ی آن؛ یعنی در زمانی که خازن به‌طور کامل در t=0 شارژ شده‌بود؛ کمتر است.

پس مقدار ثابت زمانی 1T، از شرایط شروع اولیه تا 1T همیشه 0.632 ولت یا 63.2% از شرایط حالت پایدار نهایی آن خواهدبود. به‌همین ترتیب، در 1T، ولتاژ خازن همیشه 0.368 ولت یا 36.8% از وضعیت پایدار نهایی خود پس از 5T فاصله خواهد داشت؛ زیرا یا تا VC(max) کاملا شارژ می‌شود و یا تا ۰ کاملا تخلیه می‌شود.

ما می‌توانیم افت ولتاژ را نسبت به زمان، به‌صورت گرافیکی در زیر نشان دهیم:

افت ولتاژ نمایی در طول زمان

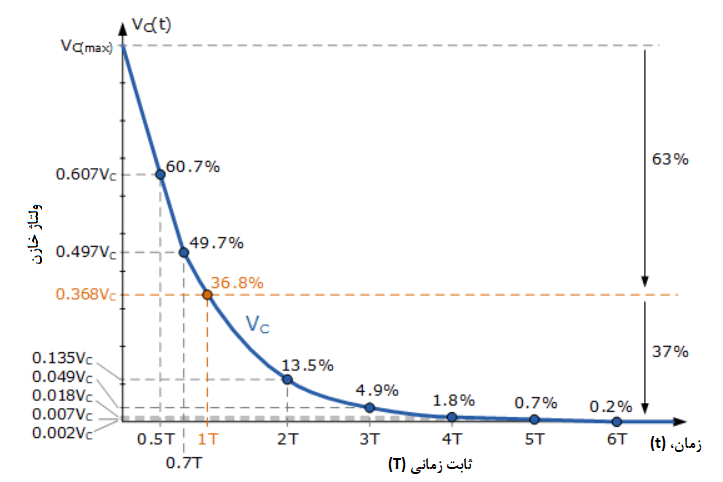
همانند قبل، نرخ افت ولتاژ در طول زمان، کاملا وابسته به ارزش ثابت زمانی RC، تاو است.

مثال شماره‌ی ۳ تاو

یک مدار RC، دارای ثابت زمانی تاو برابر با 5 میلی‌ثانیه است. اگر خازن تا 100 ولت، کاملا شارژ شود؛ حساب کنید:

1. ولتاژ دو سر خازن را در زمان‌های ۲ میلی‌ثانیه، ۸ میلی‌ثانیه و ۲۰ میلی‌ثانیه از زمانی که تخلیه شروع می‌شود.
2. زمان سپری‌شده که در آن ولتاژ خازن به ۵۶ ولت، ۳۲ ولت و ۱۰ ولت کاهش می‌یابد.

ولتاژ دو سر خازن در حال تخلیه‌ی شارژ به‌صورت زیر است:

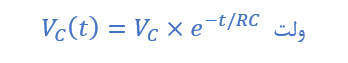
ثابت زمانی RC برابر با 5 میلی‌ثانیه داده شده‌است و از آنجایی‌که 1/RC=200 است؛ VC=100V خواهدبود.

1a) ولتاژ خازن پس از 2 میلی‌ثانیه

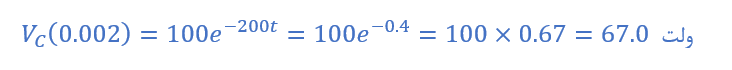
1b) ولتاژ خازن پس از 8 میلی‌ثانیه

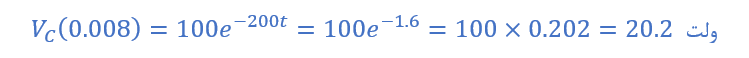
1c) ولتاژ خازن پس از 20 میلی‌ثانیه

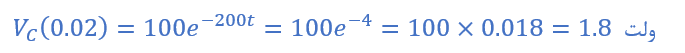
ولتاژ خازن (VC) در بازه‌ی زمانی از t=0

2a) زمان سپری‌شده (t۱) ،زمانی‌که VC(t)=56 ولت است.

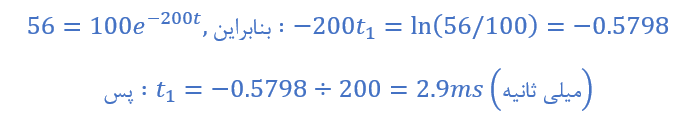
2b) زمان سپری‌شده (t۲) ،زمانی‌که VC(t)=32 ولت است.

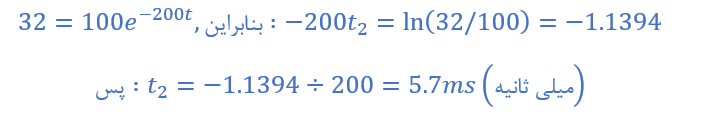
2c) زمان سپری‌شده (t۳) ،زمانی‌که VC(t)=10 ولت است.

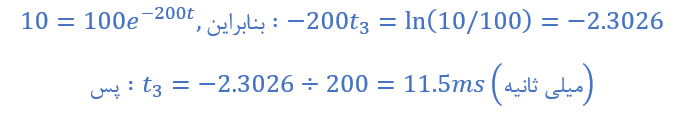
خلاصه‌ی ثابت زمانی تاو

 در این مقاله در مورد ثابت زمانی، تاو با نماد τ دیدیم؛ که پاسخ گذرا یک مدار RC، زمانی است؛ که برای تغییر از یک وضعیت حالت پایدار به حالت پایدار دیگری در شرایط ورودی، تغییر پله نیاز دارد.

هنگامی‌که، خازن از حالت ولتاژ صفر اولیه‌ی خود به ولتاژ حالت پایدار نهایی خود (V) شارژ می‌شود؛ دوره‌ی زمانی به‌صورت ᴛ=RC تعریف می‌شود؛ که حاصل‌ضرب R و C است. این امر، یک تابع رشد نمایی برای VC نسبت به ثابت زمانی RC اندازه‌گیری‌شده برحسب ثانیه، تولید می‌کند و هرچه ثابت زمانی، کوچکتر باشد؛ نرخ تغییر ولتاژ، سریع‌تر است.

ما همچنین برای یک تابع رشد نمایی دیدیم؛ که مقدار آن پس از یک ثابت زمانی،1T، برابر با 63.2% مقدار حالت مانای نهایی خواهدبود. این امر، برای یک تابع نمایی افزایشی است؛ که زمان موردنیاز برای رسیدن ولتاژ به مقدار حالت پایدار نهایی پس از 5T است.

مقدار V(t) برای یک تابع رشد نمایی در زمان t=T به‌صورت زیر داده می‌شود:

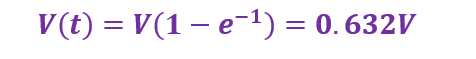
به همین ترتیب، برای یک تابع افت نمایی دیدیم؛ که مقدار آن پس از یک ثابت زمانی،1T، برابر با 36.8% مقدار حالت مانای نهایی خواهدبود. این امر، برای یک تابع نمایی کاهشی است و زمان موردنیاز برای ولتاژ است؛ تا به صفر ولت برسد.

مقدار V(t) برای یک تابع افت نمایی در زمان t=T به‌صورت زیر داده می‌شود:

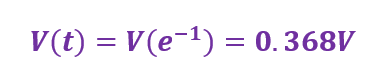
در هرصورت، از t=0 تا τ ، همیشه 63.2% از بازه‌ی زمانی و از 1T تا 5T، همیشه 36.8% بازه زمانی، درحال افزایش یا کاهش نمایی است.